基于BP神经网络的等高线生成方法

朱梅

（长江航道测量（武汉）中心，湖北 武汉 430000）

0 引言

计算机在计算和处理信息方面能力很强，但对于模式识别、感知和做出决策的能力不强，只能按事先编好的程序执行，缺乏向环境学习的能力。为此，人类依照人脑神经传导原理，探寻新的信息、存储和处理方式，设计全新的计算机处理结构模型，构造一种更接近人脑的信息处理系统。

1 神经网络综述

人工神经网络ANN模仿人脑的工作方式，它可用电子或光电元件实现，也可用软件在常规计算机上仿真。ANN是具有大量连接的并行分布式处理器，具有通过学习获取知识并解决问题的能力，且知识是分布存储在连接权中，而不是像常规计算机那样按地址存在特定的存储单元中。

1.1 神经网络节点的形式化描述

典型的神经网络如图1 所示，由一个输入层、一个输出层和多个隐藏层构成，其中每一层都包含多个单元。

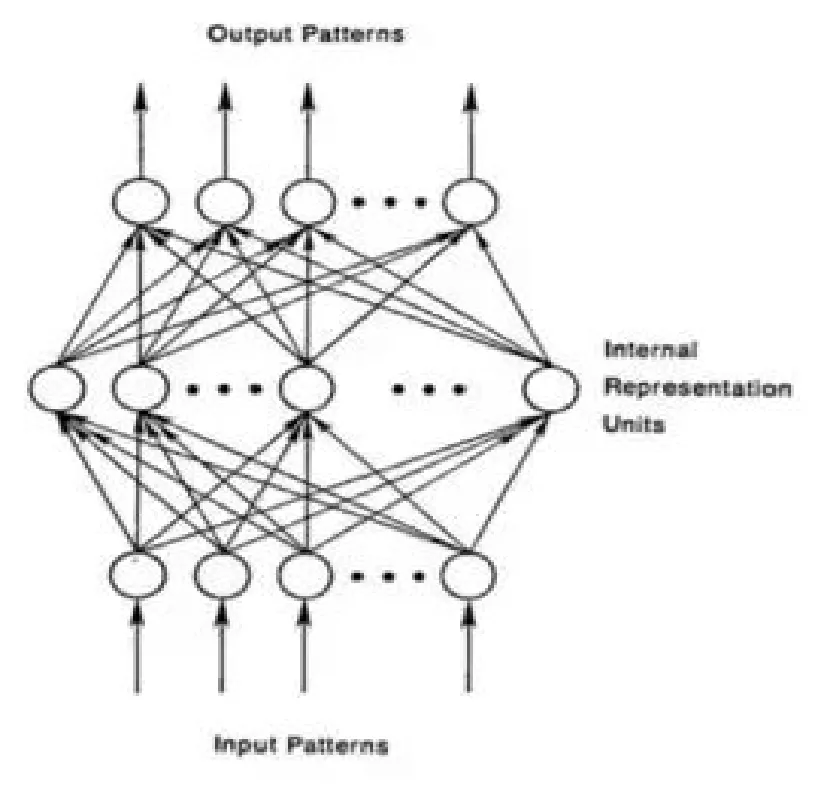
图1 典型神经网络架构示意图Fig.1 Typical neural network architecture sketch

自动编码器可以定义为由两个主要部分构成的多层神经网络。第一个部分是编码器，可以将输入数据变换成特征向量；第二个部分是解码器，可将生成的特征向量映射回输入空间。

基本的人工神经网络神经元可以和前一层神经网络层中的所有神经元有连接，每个连接都有各自的权重，权重通常是随机值[1]。和这个神经元连接的所有神经元的值都会乘以各自对应的权重，然后把这些值都求和。在此基础上，额外加一个bias，可以避免输出为零的情况。bias也是一个数字，经常是一个常量（-1或者1）。这个总和最终被输入到一个激活函数，这个激活函数的输出最终就成为这个神经元的输出。

1.2 分析工具

人工神经网络系统由于具有信息的分布存储、并行处理以及自学习能力等优点，已在信息处理、智能控制等领域得到广泛的应用。尤其是 BP神经网络，可以任意精度逼近任意连续函数，所以广泛地应用于非线性建模、函数逼近和模式分类等方面。但利用神经网络解决实际问题时，必定会涉及到大量的数值计算问题。Matlab软件为解决数值计算与计算机仿真之间的矛盾，推出了一套高性能的数值计算和可视化软件包。其中的神经网络工具箱是以神经网络理论为基础，用 Matlab 语言构造出典型神经网络的工具函数。

2 现有的等高线生成方法

目前普遍使用的等高线生成方法为数字高程模型内插方法。数字高程模型DEM从本质上是关于地表的一个数学函数，DEM内插就是根据若干已知相邻参考点的高程求出待定点上的高程值。

2.1 等高线离散化法

等高线离散化法是将等高线数据视为离散化的数据点，利用这些离散数据内插得到各种格网点的高程值。在一定范围内搜索落在其中的已知点数据，并计算它的加权平均值。在此基础上，还有两种修正方法：一种是沿预定轴方向搜寻与等高线的交点，利用这些交点坐标内插出格网点高程；另一种是沿内插点陡坡度内插[2]。

2.2 不规则三角网（TIN）法

TIN法通过一系列互不交叉、互不重叠的三角面来逼近物体表面，它充分考虑了等高线自身的特征，能够顾及地形特征，可以灵活的适应任意复杂的图形数据，同时速度很快[3-4]。

2.3 等高线生成DEM的高精度方法

对原始等高线位置利用形态变换进行保护，使得原始等高线信息得以保护；将矢量等高线数据栅格化，并记录相应矢量数据的特征值，将地形分为七类，对不同的地貌类型选择不同的结构元素对等高线的栅格图像进行多刻度距离变换，从而得到相应的DEM[5-6]。

内河航道图的等深点生成有其特定的规律，以上方法作为应用于普通地形图的等高线生成方法，算法过于粗糙。本文提出的算法，是根据已有的电子航道图建立神经网络系统，寻找高程点与水深点之间的关系，来生成新的高程点。与数字高程模型内插方法相比，该算法更接近实际工作需求。

3 神经网络生成等高线算法

3.1 训练样本

3.1.1 水深点点集 A

图2中选中的点是（3305785,640745，-0.8）。水深点点集 A产生方式是，由外业测量员用测量仪器采集。

图2 水深点点集Fig.2 water depth Point set

3.1.2 等深线点集 B

图3中选中的点是（3305803,640759，-0.1）。等深线点集 B产生方式是，在A点集导入eps软件后，由内业绘图员人工定点的。把B点集中z值相同的点连接起来，就是等深线。

图3 等深线点集Fig.3 The Contour point se

3.2 神经网络系统设计

设计神经网络系统，能以水深点集作为输入，输出等深线点集。本次实验中，以两个相邻的水深点a1、a2的坐标以及这两个点之间的等高线点b坐标作为输入；以等高线点b的x坐标作为输出[7-8]。

3.2.1 输入输出层的设计

将18组点坐标作为输入，将对应的等高线点b的x坐标作为输出。所以输入层的节点数为8，输出层的节点数为1。

3.2.2 隐层设计

有关研究表明，有一个隐层的神经网络，只要隐节点足够，就可以任意精度逼近一个非线性函数。本文采用含有一个隐层的多输入单输出的BP网络建立预测模型。本文在选取隐层神经元个数的问题上参照了经验公式：。n为输入层神经元个数，m为输出层神经元个数。由上式可计算出神经元个数为（4，13），本实验选择隐层神经元个数为6。

3.2.3 激励函数的选取

BP神经网络通常采用Sigmoid可微函数和线性函数作为网络的激励函数。由于网络的输出归一到[-1,1]范围内，因此预测模型选取S型对数函数tansig作为输出层神经元的激励函数。

3.3 模型实现

本文选取2017年3月鲤鱼山水道图，中的部分水深点和等深线点，如表1。由此预测序号18号等高线点b的x坐标。

表1 坐标Table 1 coordinates

此次预测选用MATLAB中的神经网络工具箱进行网络的训练，预测模型的实现步骤为：将训练样本数据归一化后输入网络,设定网络隐层和输出层激励函数分别为tansig和logsig函数，网络训练函数traingdx，网络性能函数为MES，隐层神经元数初设为6。设置网络参数:网络迭代次数epochs为5000次,期望误差goal=0.00000001,学习速率lr=0.01。设置参数后,开始训练网络，通过24次重复学习达到期望误差后完成学习。完成网络训练后，将各项指标输入网络，就能得到预测数据[9]。matlab代码如图4。

图4 matlab代码Fig.4 matlab Code

预测结果为：c=3304012。

4 分析与展望

4.1 误差分析

本次计算的结果为：3304012，实际结果为3305141。相对误差率:（3305141-3304012）/3305141=0.3%

4.2 改进方向

4.2.1调整隐层数量

本文中采用的单隐层神经网络，较为简化。神经网络计算可以进行深度学习，提高准确性。深度学习结构一般有多个隐层通过非线性方式来连接。深层结构的效果优于浅层结构，其中的重要原因是多隐层的网络结构对数据有更好的表示能力，能通过逐层的特征提取将数据表示得更加抽象，从而提高模型的准确性。

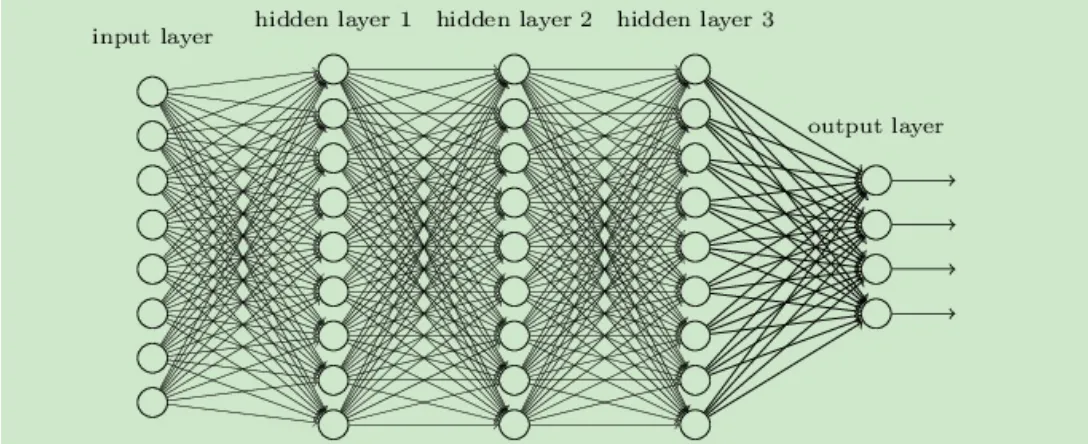
图5 多隐层的网络结构Fig.5 The network structure of the multi-hidden layer

但当隐层数量过高时，准确率可能会下降。用ResNet可以解决这个问题，它引入了残差网络结构，使之不再是多个隐层的堆叠，而是通过短连接来连接输入和输出。这样的网络可以达到百层乃至千层的量级，并且不会出现梯度消失现象。

4.2.2 对高程点进行聚类

在建立预测算法之前，用聚类算法对高程点进行处理，能得知用哪些高程点作为系统输入更合理。本次实验中直接选取的相邻最近的两个高程点，实际上用聚类算法之后该系统能得到优化。

4.2.3 寻找合适的损失函数

可以用一个合适的损失函数来度量训练样本的输出损失，接着对这个损失函数进行优化求最小化的极值，对应的线性系数矩阵W、偏倚向量b即为最终结果[10]。

5 结论

利用MATLAB进行BP网络模型建立，将已知高程点、水深点坐标作为输入，以等高线点b的x坐标作为输出，实验结果证明了该模型用于等高线生成的可行性。