Ⅰ-型笼合物Ba8Ga16Ge30笼的应变声子谱

宋阳,苏耀恒,夏明岗,程琳,吕正

(1.西安交通大学 理学院,陕西 西安 710049;2.西安工程大学 理学院,陕西 西安 710048)

0 引言

电子晶体-声子玻璃材料提出后,笼合物成为研究热点[1-5],作为新型的热电材料,笼合物材料具有比以往材料较高的电导率,较低的热导率[6-11]。目前对Ⅰ-型笼合物的热导率研究取得很大进展。以研究Ga-Ge型材料为主,它们的热导率很低。20世纪初期Kuznetsov等[12]在研究 Ba8Gal6Ge30的高温热电性能时推测 Ba8Gal6Ge30在温度300～850 K的热导率大约为22.4 W/mK,在低温下其热导率更低。Hou等[13]实验发现Ba8Gal6Ge30材料在Ga/Ge不同配比下温度300～850 K热导率约为1.43～2.19 W/mK。其后自纳米材料兴起,研究者发现纳米级Ba8Ga16Ge30热导率更低[14-15],笼合物材料的热导率取得进一步的发展。然而目前没有研究显示应变下Ba8Ga16Ge30热学性质.本文基于晶格动力学方法构建模型计算了应变下的Ba型Ga-Ge基笼合物的声子谱。笼合物类材料的结构复杂,目前理论研究都是基于第一性原理,这种方法计算量大,数据结果物理机理分析困难。因此,本文使用简化模型结合物理近似的方式对Ba型Ga-Ge基笼合物声子应变,探究内在物理机理。研究中未考虑振颤子的作用,笼合物笼内空间大,应变对振颤子影响微小,可以忽略。据此,提出采用应变的方式来调控Ba8Ga16Ge30材料的热学性质,以期实现材料热调控的同时提高它的热电转换效率。

1 模型建立

笼合物体前景广阔,但其体系庞大,导致理论研究的局限性,研究人员也在尝试解决这一问题。2008年Christensen[16]课题组以构建模型的思路研究笼状材料,定性地给出了材料的声子谱,并就其物理机理做出解释。

表1 Ge/Ga原子坐标及分布比例[15]

笼合物每个原胞由六个十四面体和两个十二面体组成,多面体之间通过共面连接。笼合物原胞中原子数目繁多,在此对结构进行简化,建立简单合理的物理模型.如图1(a)是Ba8Ga16Ge30的结构图,外层的小球代表基原子Ga/Ge,中心的大球代表填充原子Ba.以填充原子所处层面划分,取(100)晶面简化如图1(b),将十二面体和二十六面体构成的笼看成质量分别为m、M的硬球,图中两种硬球分别用蓝色和黄色表示,笼合物简化为二维结构。建模层的多面体排列组合成二维结构,结构中包含两种原子。根据笼子结构得出这两种原子的约化质量,采用Tersoff势[17-19]计算二维模型中原子之间的势能。

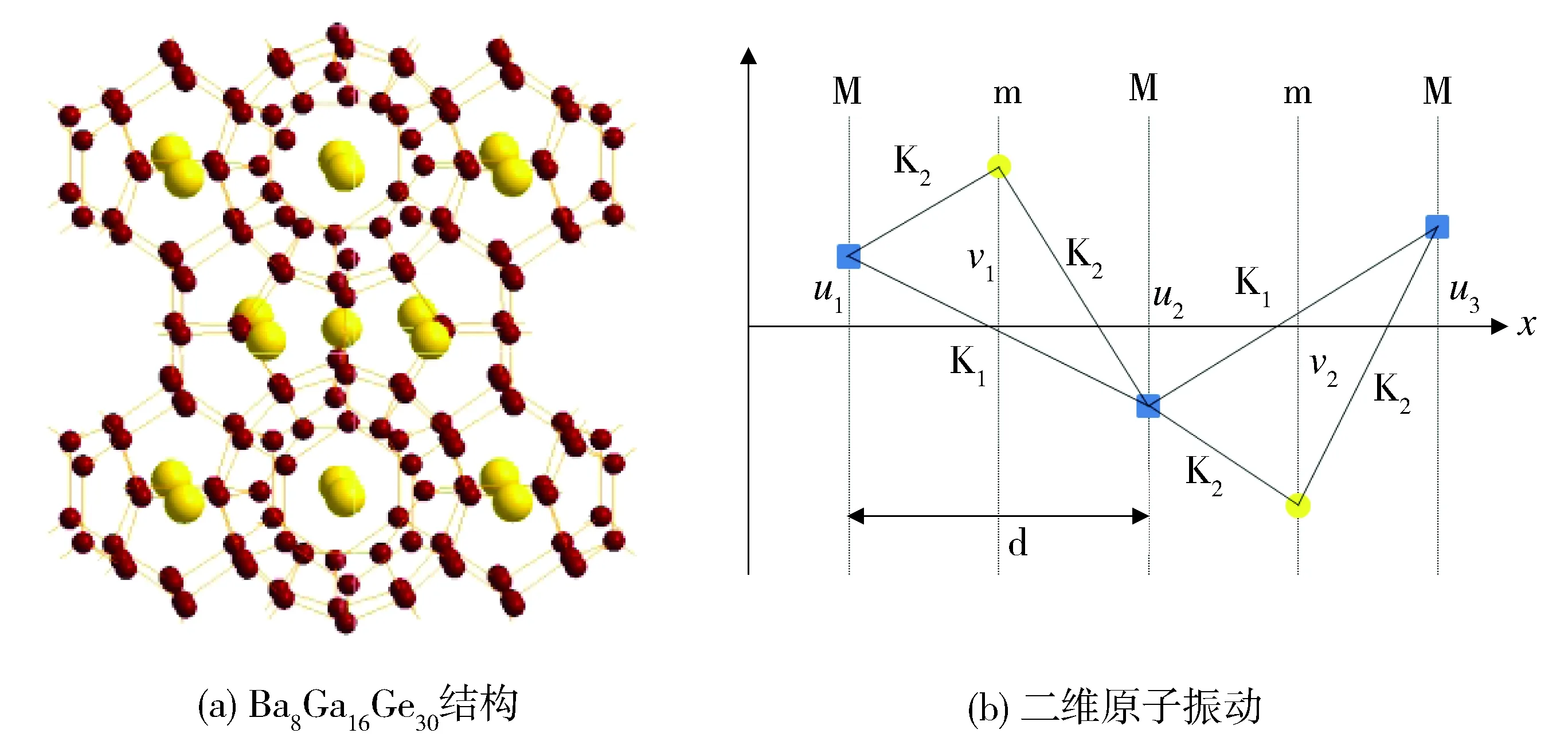
Fig.1 Stucture of Ba8Ga16Ge30图1 Ba8Ga16Ge30结构

构成十二面体的小原子质量为m,构成二十六面体的大原子质量为M。两个大原子之间具有相互作用力,大原子与小原子之间也有相互作用力,但由于小原子与小原子距离较远,其间没有相互作用。 取出二维模型的原胞,每个原胞中有四个原子,两个M原子和两个m原子,其中a1,a2分别表示晶格基矢,并有a1=2a2。

简化原子的质量可以用经典的密度体积法。Ga、Ge原子质量大小几乎一样,又是按一定概率分布的,因此两种原子在原胞中的分布可以看成均匀分布。那么原子的质量为:抽象出的原子质量=质量密度×体积。这样可得到两种约化原子的质量。

(1)

通过几何学计算得到十二面体的体积和二十六面体的体积,最终求得大小硬球的约化质量分别为317.907, 885.723。

Tersoff是半经验势,是一种键级势,描述原子相互作用键的强弱变化。具体来说,如果与某个原子相近邻的原子增多,则该原子与其它原子间所成的键势就会减弱。根据Abell的描述,一个多体系统的结合能可以写成的原子对相互作用之和,而这些对相互作用必须要受到原子所处的局域环境修正。

Vij=fc(rij)[fR(rij)+bijfA(rij)]

(2)

其中rij是i与j原子间的距离,Vij是两原子的相互作用势,这个势函数包括吸引和排斥函数。fc(rij)对相互作用限定在一个范围内,截断函数采取光滑形式。根据原子势理论计算得到小球之间的作用力常数。

(3)

2 声子谱

2.1 无应变声子谱

晶格动力学理论得到格波频率由系数行列式等于零决定[20]。由此即可得到Ba8Ga16Ge30材料笼子的色散关系图。

Fig.2 Phonon dispersion of Ba8Ga16Ge30framework(a)Ba8Ga16Ge30笼(100)面声子谱；(b)原子振动方向图2 Ba8Ga16Ge30笼声子谱

图2左图表示Ba8Ga16Ge30笼布里渊区色散曲线,Γ→X,X→M以及M→Γ三个高对称方向的频率,频率在0～270 cm-1范围。Γ→X方向有八支声子,其中两支声学声子 LA和TA;六支光学声子LO和TO。两支声学声子几乎成线性,并且非常接近。六支光学声子中有两支随波矢不同,变化较大,其它基本保持水平的,符合光学声子的一般规律。在X、M两个高对称点处是二重简并的。图2右图表示格波的原子运动情况,这里标出四个低频声子的原子运动。序号1, 2, 3, 4分别代表原胞中的四个原子。两支声学声子代表原胞内原子的同向运动。后面两支是光学声子的原子运动,可以看出光学声子代表原子相对运动。

2.2 应变声子谱

材料加应变之后,导致其结构发生变化,进而影响它的性质.具体来说,加应变后晶体原子间距发生变化,势能改变,此时它们相互作用力常数也随之改变,引起色散关系改变。根据胡克定律得到单轴和切方向的应变张量计算应变后模型的力常数。

Fig.3 Phonon dispersion of Ba8Ga16Ge30framework under uniaxial strain(a)沿x方向拉伸5%,10%的应变声子谱；(b)沿x方向压缩5%,10%的应变声子谱；(c)沿y方向拉伸5%,10%的应变声子谱；(d)沿y方向压缩5%,10%的应变声子谱图3 沿单轴应变Ba8Ga16Ge30笼声子谱

图3表示材料应变后的格波谱。图3(a)与(b)分别表示沿x方向拉伸应变谱和压缩应变谱,图3(c)与(d)分别表示沿y方向拉伸应变谱和压缩应变谱。黑色表示不加应变曲线,红色和蓝色分别表示拉伸5%和10%的曲线,黄色和绿色表示压缩5%和10%的曲线,色散图形中,所有谱线都用规定的颜色区分,以后的文章中用到的不再作一一说明。

图3(a)每支声子的频率都是随拉伸应变降低的,应变越大,声子频率变化越大。单轴的应变并未破坏它的简并性,M点处,无论是拉伸5%或是10%,它的简并依然很完美。图3(b)是压缩应变导致声子频率增大,呈现出应变越大,变化越大的规律。拉伸导致原子间距增大,原子间相互作用势能减弱,则两原子间的力常数变小,声子频率减小。反之,压缩减小了原子间距离,进而增大了原子间的力常数,声子频率增大。另外,TA声子没有LA声子变化大.不难理解,沿x方向加应变后,x方向的振动变化是比较明显的,故LA声子的变化应该比TA声子变化更加明显。

Fig.4 Phonon dispersion of Ba8Ga16Ge30framework under shear strain图4 Ba8Ga16Ge30笼切应变的格波谱

与沿x方向应变规律一致,沿y方向拉伸应变导致频率降低,压缩应变使得频率增大,并且应变越大,声子频率变化越大。沿y方向的应变很好地保持了其简并性。材料中原子的位置影响力常数的变化,原子在沿x方向上的键长贡献多,因此沿x方向的应变要比沿y方向的应变影响大,导致y方向的应变简并性更完美。与沿x方向的应变恰恰相反,此时TA声子的变化远大于LA声子,其原因就是y方向上加应变后,y方向的振动是有明显变化的。

图4表示切应变的格波谱,很明显它与沿单轴应变的声子谱不一样。它已不再遵循单纯的应变规律.随应变,频率的变化比较杂乱,但依然存在一些规律,纵振动声子频率随应变增大,横振动声子随应变减小,应变越大,变化越大。这是由材料的结构决定的.同样,在两个高对称点处依然简并,但在X→M方向上,简并破坏。

3 结论

笼合物晶胞结构复杂,体系庞大,一般的软件计算也只能得到一些数据结果,很难把握其物理机理,本文对其进行简化,建立新的模型结构进行计算。建模的过程是科学合理的,用晶格动力学理论得到声子色散关系。另外,对材料加应变,改变了材料结构,具体来说就是改变了原子间距,使得力常数有变化,导致格波频率改变,应变对笼合物的热学性质有影响,在后期的工作中继续研究,期待能够用应变的方式调控笼合物的热学性质。