青海湖流域景观格局空间粒度效应分析

翟 俊, 侯 鹏, 赵志平, 肖如林, 颜长珍, 聂学敏

(1.环境保护部卫星环境应用中心，北京 100094； 2.中国环境科学研究院，北京 100012； 3.中科院寒区旱区环境与工程研究所，兰州 730000； 4.青海省生态环境遥感监测中心，西宁 810007)

0 引言

随着我国自然生态与环境保护工作的不断深入，流域生态系统已经成为我国生态监管与环境宏观管理的重要调控单元[1]。流域空间的各类生态系统分布及其景观格局直接影响到流域生态系统服务功能、生态系统质量等所有方面的好坏。景观格局反映了不同大小和形状等空间特征的景观要素的空间分布情况，不同景观具有不同景观格局特征。多尺度的自然和社会中普遍存在的空间异质性特征，即尺度问题在景观生态学相关问题研究中至关重要，尺度选择直接关系到结果的可靠性[2-3]。在景观生态学中，尺度通常包括空间粒度(尺度)和时间粒度(幅度)2方面，其中空间粒度表示研究区空间最小可辨识单元所代表的特征长度、面积或者体积。

在空间统计学方法、景观格局指数法和分维分析法等[4-5]景观生态学多尺度分析方法中，景观格局指数法因其高度浓缩景观格局信息，可以较好地反映不同景观要素的空间配置关系而定量衡量景观格局状况的优劣，在河流湿地[6-7]、地形地貌[8]、城市热岛[9]等各类土地利用与景观生态领域得到广泛应用[10-11]。所以许多研究案例通过分析景观格局指数的空间粒度效应来反映景观格局的空间粒度效应，将景观格局指数与空间粒度之间的关系演变为景观尺度效应关系。研究发现不同空间粒度与景观格局指数之间具有显著的尺度效应，且在不同的研究区和研究对象中并不具有普适性[12-15]，如大辽河流域湿地景观格局的最佳分析粒度为60 m[16]，黑龙江巴彦县景观格局最佳分析粒度为100 m[17]，珠三角城市热岛格局特征的临界粒度为150 m[9]等。因此如何选择最为适宜的空间粒度，从而客观真实的反映出景观格局状况，成为景观生态学的关键问题之一[18-20]。国内外学者先后提出了拐点识别法和信息损失评价等方法，从定性评价过渡到定量评价[21-23]，同时也发展出二者相结合的方法，综合选取最适宜的空间粒度[16]，从而在该粒度条件下既能有效反映景观格局，也尽可能减少信息损失，尽量避免和消除尺度效应对景观格局分析的影响。

青海湖流域位于青藏高原东北部，是世界上典型的高寒湿地自然保护地，对于维持青藏高原东北部水源涵养和生物多样性服务功能，以及区域生态安全具有重要作用。相关研究表明，青海湖流域湿地对降水变化更为敏感[24]，并且具有较高的水源涵养价值[25]。但不同研究结果中，区域或生态系统的价值估算差异较大[25,26]，其数据源的空间尺度或者粒度的差异，是影响评价结果的重要因素之一。然而，目前景观格局尺度或粒度的分析与应用多见于人类活动明显的流域或者城市化区域[9,16-17,22-23,27]，对以气候变化为主要影响，并且对维系区域生态安全的青海湖流域，相关研究还很缺乏。本文以青海湖流域为研究区，通过选用一些常用景观格局指数，比较不同指数对空间粒度变化的响应差异，从而识别流域尺度景观格局分析研究中的空间粒度效应，通过综合拐点识别和信息损失评价方法，提出流域尺度景观格局分析的最适宜空间粒度，为统一流域尺度生态服务功能和价值评估的生态指标，实现生态保护监管统一化管理提供参考和依据。

1 资料与方法

1.1 研究区概况

青海湖流域总面积约为2.96万km2，地处青海省西部柴达木盆地、东部湟水谷地、南部江河源头与北部祁连山地的枢纽地带，地势西北高、东南低，流域内地势海拔高差为2 097 m。青海湖流域是青藏高原东北部的特殊生态功能区，在区域生态系统中拥有着重要地位。流域内青海湖为我国最大的咸水湖和内陆湖，对区域气候有着重要的影响。流域位置如图1所示。

图1 青海湖流域地理位置Fig.1 Geographical location of Qinghai Lake watershed

1.2 数据源及其面向对象信息提取

选取美国陆地资源卫星Landsat5搭载的TM传感器和我国环境与灾害监测预报小卫星HJ-1卫星搭载的CCD传感器获取的光学卫星遥感数据为主要数据源，空间分辨率均为30 m。在影像分割的基础上，根据不同土地覆被类型的光谱特征，建立卫星遥感影像的分类规则集。对于光谱复杂的类型，采用最邻近方法进行类别划分，从而实现基于面向对象分类方法的地表景观信息提取，得到流域地表实际景观分类信息。通过分层随机抽样和野外采集实地景观类型信息，进行了分类结果精度验证，分类总精度为91%。

1.3 尺度效应分析与最佳粒度选取

对基于遥感解译得到的实际景观信息图像，采用面积最大法进行重采样，获得具有不同空间粒度的景观分类数据。利用FragStats软件计算得到景观格局指数值，绘制不同空间粒度下的指数曲线，分析景观格局指数的尺度效应； 然后，利用拐点法和信息损失评价方法，分析确定最佳(最适宜)的景观格局分析粒度的大小。信息损失评价模型为[16]

(1)

式中：P为某一个评价指标的信息损失百分比；M为该评价指标的信息损失总量；Ab为所有景观类型该评价指标的基准数据(30 m空间分辨率)值之和；Agi为第i类景观该评价指标的栅格数据值；Abi为第i类景观该评价指标的基准数据值；n为景观类型的总数目。

2 结果与分析

2.1 景观格局指数的空间粒度效应

由于景观类型数据是基于30 m空间分辨率的卫星数据提取得到的，空间粒度重采样时，以30 m为起始，1 500 m为终点，30 m为间隔，采用面积最大法将景观类型数据栅格化，得到50幅不同栅格大小(空间粒度)的景观类型数据。举例30 m，480 m，930 m，1 200 m和1 500 m空间粒度景观类型分布如图2所示。

从流域尺度生态特点出发，结合不同景观格局指数的生态学意义，选取24个具有代表性的景观格局指数，利用FragStats软件分别计算得到不同空间粒度下的景观格局指数值(表1)。

通过绘制不同空间粒度下的景观格局指数曲线，即景观格局指数的空间粒度效应曲线，可以看出，随着空间粒度的变化，流域景观格局指数都有明显的变化，景观格局指数的空间粒度效应呈现出不同的变化特征和规律。总体上，空间粒度效应可以归纳为6类，分别是幂函数、二次函数、对数函数、线性函数、分段函数和稳定且变化幅度增大型。

(a) 30 m×30 m (b) 480 m×480 m

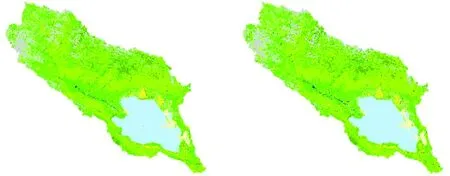
(c) 930 m×930 m(d) 1 200 m×1 200 m

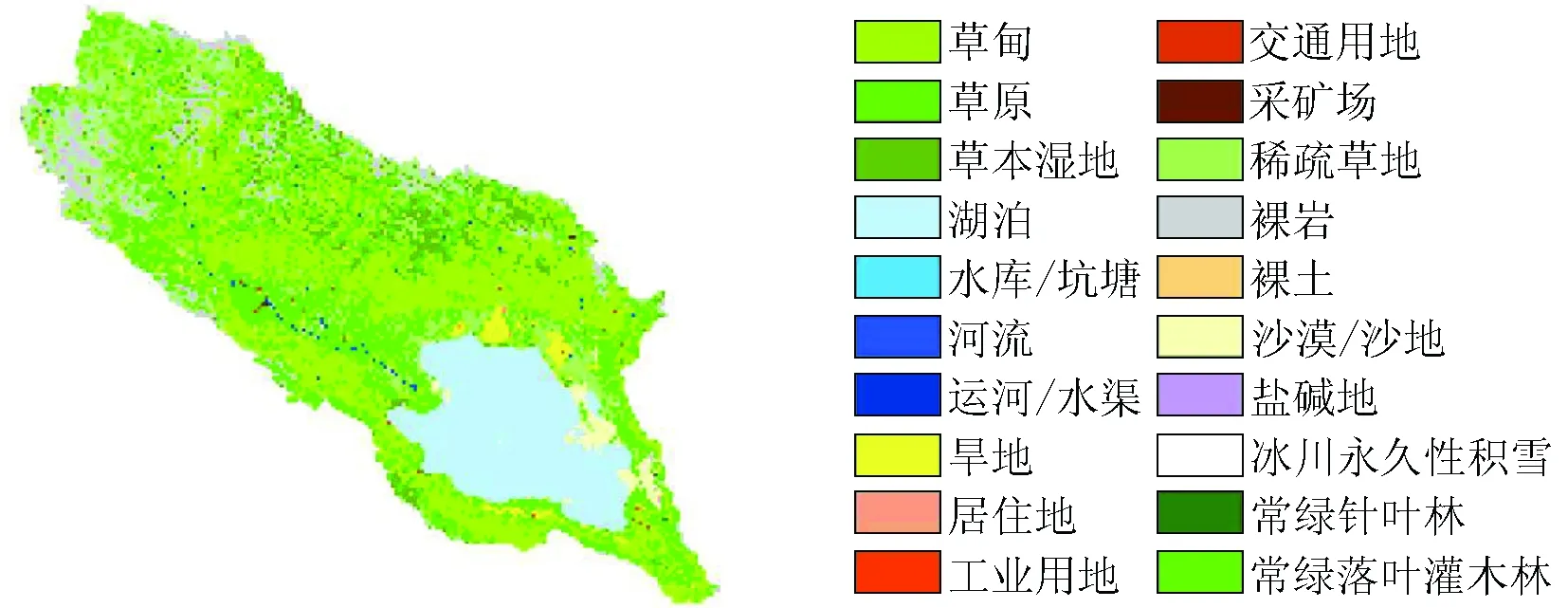
(e) 1 500 m×1 500 m

图2 青海湖流域不同空间粒度景观举例Fig.2 Examples of landscape in different grain sizes表1 主要景观格局指数及其空间粒度变化的拟合函数Tab.1 Functions of landscape indexes and grain sizes

24个景观格局指数的空间粒度效应中有14个呈现出幂函数下降特征，具体如图3所示。

(a) 景观形状指数(b) 边界总长度

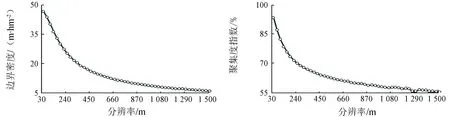
(c) 边界密度(d) 聚集度指数

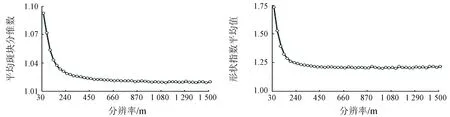
(e) 平均斑块分维数 (f) 形状指数平均值

图3-1典型景观格局指数的空间粒度效应曲线(幂函数型)

Fig.3-1Statisticcurvesofdifferentlandscapeindexeswithdifferentgrainsizes(powerfunctiontype)

(g) 蔓延度指数(h) 景观分割度

(i) 分离度指数(j) 斑块数

(k) 斑块密度(l) 面积加权形状指数

(m) 斑块面积变异系数(n) 面积加权平均斑块分维数

图3-2典型景观格局指数的空间粒度效应曲线(幂函数型)

Fig.3-2Statisticcurvesofdifferentlandscapeindexeswithdifferentgrainsizes(powerfunctiontype)

由图3可知，景观形状指数、边界总长度、边界密度、聚集度指数的空间粒度效应更为相似。与这4个指数相比，平均斑块分维数和形状指数平均值更为相似，2个指数的空间粒度效应在180～240 m之间出现“拐点”，拐点之前降低趋势较为显著，拐点之后降低趋势变缓。蔓延度指数、景观分割度、分离度指数的总体变化趋势与景观形状指数等4个指数相似，但是不同空间粒度条件下的景观格局指数值呈现出一定的摆幅，尤其是景观分割度和分离度指数摆幅较大。斑块数、斑块密度、面积加权形状指数、斑块面积变异系数和面积加权平均斑块分维数等的空间粒度效应特征相似，呈现出随空间粒度变粗，景观格局指数先暂时增长后总体幂函数下降的特点，“拐点”分别出现在60 m，60 m，150 m，150 m和60 m处，并且面积加权形状指数、斑块面积变异系数和面积加权平均斑块分维数等3个指数的下降过程中呈现出一定的波动变化。

随着空间粒度的变化，有4个景观格局指数的空间粒度效应呈现出不同的特征。平均斑块面积呈现出二次多项式函数增长的特点，边缘面积分维数呈现出对数函数增长的特点，斑块面积标准差和平均欧几里得最近距离呈现出线性变化函数增长的特点(图4)。

有6个景观格局指数的空间粒度效应变化无法用函数规律描述。其中，最大斑块指数呈现出分段阶梯式增长的特点，段点位于660 m空间粒度处。斑块丰富度和斑块丰富度密度呈现出分段阶梯式下降的特点，斑块丰富度的断点位于450 m和870 m，斑块丰富度密度的断点位于450 m。景观面积、Shannon多样性指数和Simpson多样性指数等的变化特点相似，趋势基本稳定，但是随着空间粒度的变化，变化幅度愈来愈大(图5)。

(a) 平均斑块面积 (b) 边缘面积分维数

(c) 斑块面积标准差 (d) 平均欧几里得最近距离

图4典型景观格局指数的空间粒度效应曲线(二次函数、对数函数、线性函数型)

Fig.4Curvesofindexeswithdifferentgrainsizes(quadratic,logarithmicandlinearfunction)

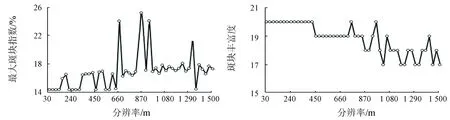
(a) 最大斑块指数(b) 斑块丰富度

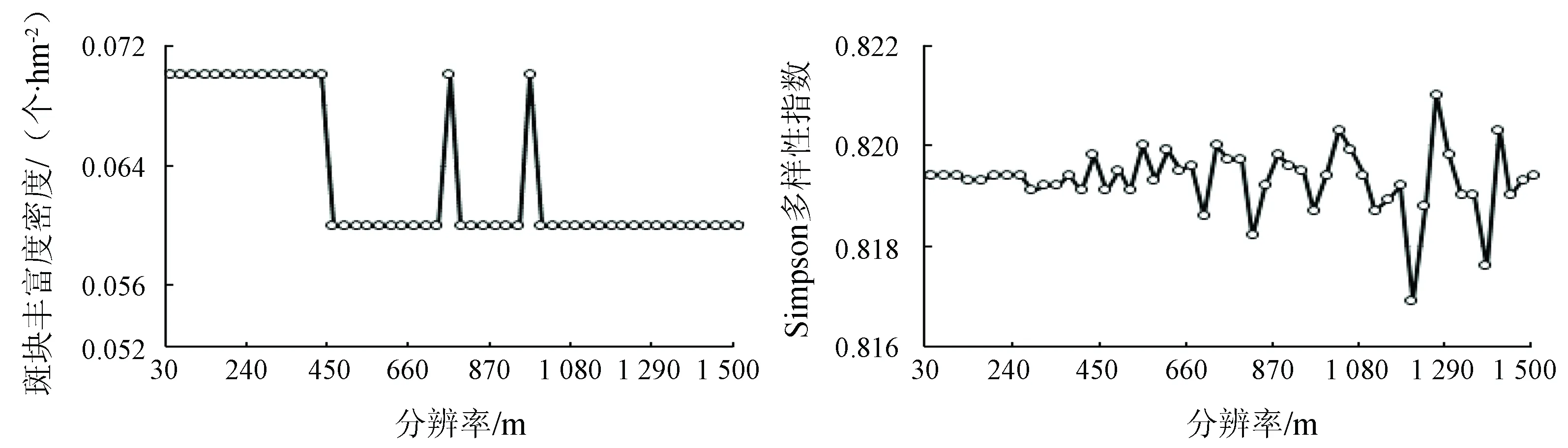
(c) 斑块丰富度密度 (d) Simpson多样性指数

(e) 景观面积 (f) Shannon多样性指数

图5典型景观格局指数的空间粒度效应曲线(分段函数、稳定且变化幅度增大型)

Fig.5Curvesofindexeswithdifferentgrainsizes(piecewisefunctionandstabletypewithincreasingrangeofchange)

2.2 最佳空间粒度的选取

对于同一流域景观，空间粒度的大小直接影响到景观格局分析结果的科学性和合理性，从而影响到对流域生态系统各组成单元的组成特征和空间配置关系的客观了解，进而影响对流域生态景观的功能和动态过程的理解。基于景观格局指数方法的景观格局分析研究，主要利用不同的景观格局指数从单个斑块、斑块类型和景观水平等3个不同层次的景观格局。研究景观格局指数的生态学意义和计算方法，可以看出相当一部分景观格局指数是基于景观面积、斑块数量和边界长度等斑块类型的基本属性特征信息，基于不同的数学统计方法计算得到的。在一定程度上，可以理解为是景观面积、斑块数量和边界长度的衍生指数。为此，选择景观面积、斑块数量、边界长度为核心指标，基于信息损失评价模型，可以计算得到随着空间粒度变化而引起的信息损失情况，统计曲线如图6所示。

图6 空间粒度效应引起的景观格局指数信息损失Fig.6 Information loss of landscape indexes caused by the grain size effect

从统计曲线可以看出，随着空间粒度的变化，景观面积、斑块数和边界总长度3种景观格局指数的信息损失量总体增加，但是变化趋势有所不同。景观面积指数随着空间粒度的增加，信息损失量呈现出线性增加趋势，但是变化幅度远小于其他2个景观格局指数的信息损失量，第一个显著的拐点出现在150～210 m处，信息损失量仅为0.08%。斑块数量和边界总长度景观格局指数信息损失量呈现出对数增加趋势，二者的变化幅度远远大于景观面积指数的变化幅度。斑块数量和边界长度的信息损失量曲线在150～180 m之间有个交点。在该点之前，边界长度指数的信息损失量总体大于斑块数量的信息损失量，且二者都在60 m和90 m处出现了明显拐点； 在该点之后，斑块数量的信息损失量大于边界长度指数的信息损失量，并且呈现出再次相交的趋势特征。考虑随着粒度减小，数据量呈现级数增长，降低计算效率[21]，因此综合3种景观格局指数信息损失量的变化特征，青海湖流域景观格局分析的空间粒度以90 m为最佳选择。

3 结论

流域是生态系统中的一个重要尺度和基本单元，空间粒度效应分析及最佳空间粒度选取是流域尺度景观格局分析与评价的关键。本文以青海湖流域为研究区，通过卫星遥感的面向对象分类方法解译获得景观类型数据，以30 m为起始，1 500 m为终点，30 m为间隔，得到不同空间粒度下的景观类型数据，利用FragStats软件计算得到景观面积等24个景观格局指数，绘制不同空间粒度下的景观格局指数曲线，分析景观格局指数的尺度效应。综合考虑景观格局指数—空间粒度之间的统计曲线和信息损失情况，利用拐点法和信息损失评价方法，从而确定最佳(最适宜)的景观格局分析粒度的大小。结果表明：

1)随着空间粒度的变化，流域景观格局指数都有明显的变化，景观格局指数的空间粒度效应呈现出不同的变化特征和规律。总体上，空间粒度效应可以归纳为6类，分别是幂函数下降、二次多项式函数增长、对数函数增长、线性函数增长、分段阶梯函数下降或增长、稳定且变化幅度增大型。空间粒度效应以幂函数下降为主，24个景观格局指数中有14个呈现出这种特征。

2)景观面积、斑块数和边界总长度等3种景观格局指数的信息损失量总体增加，但是变化趋势有所不同。随着空间粒度的变大，景观面积指数信息损失量呈现出线性增加趋势，斑块数量和边界长度景观格局指数信息损失量呈现出对数增加趋势，且二者的变化幅度远远大于景观面积指数的变化幅度。综合3种景观格局指数信息损失量的变化特征，流域景观格局分析的空间粒度以90 m为最佳选择。