含水率对构造煤煤粒瓦斯扩散的影响研究*
张庆浩,贾天让,3,李松林,魏国营,3
(1.河南省瓦斯地质与瓦斯治理重点实验室—省部共建国家重点实验室培育基地,河南 焦作 454000;2.河南理工大学 瓦斯地质研究所,河南 焦作 454000;3.全国煤炭行业瓦斯地质与瓦斯防治工程研究中心,河南 焦作 454000;)
0 引言
水力化措施是处理瓦斯危害的一种重要的技术措施,如煤层注水、水力冲孔、水力钻割、水力割缝、水力压裂和水力挤出等[1-4],水力化措施的实施增大了煤岩体内部孔隙裂隙,提高了瓦斯抽采效率,然而水力化措施增透的同时,高压水增大了煤层含水量,水分对瓦斯解吸扩散“促进”和“抑制”作用仍不明确。构造煤的瓦斯含量测定结果往往偏小,水分是构造煤瓦斯解吸规律的重要影响因素之一。因此,研究不同水分对煤粒瓦斯扩散的影响,优选适合描述含水煤粒瓦斯解吸全过程的扩散模型,对煤矿瓦斯灾害防治和煤层气勘探具有重要意义。
目前众多学者对不同含水率煤粒瓦斯解吸扩散规律和扩散模型做了大量研究。聂百胜等[5]通过水蒸气吸附法研究得到水分作用下,煤体瓦斯解吸能力大幅度降低;极限瓦斯解吸量、初期解吸率、初始扩散系数均随水分含量的增加而减小;牟俊惠等[6]通过试验研究了不同含水率条件下瓦斯解吸初速度的变化规律,试验结果表明煤样的瓦斯解吸初速度与煤样内含水率呈对数关系;陈攀等[7]通过改变吸附平衡压力、变质程度和破坏类型等条件,研究了不同水分条件下的煤样瓦斯解吸规律,得出了水分影响的校正系数并进行了验证;陈向军[8]在自制的实验装置上对不同外加水分煤样瓦斯解吸过程进行了测试,实验结果表明外加水分对卸压后煤的瓦斯解吸具有抑制作用。在瓦斯扩散模型方面,大多数学者偏重用单孔隙扩散模型、双孔隙扩散模型等来形象描述瓦斯的扩散过程[9],单一孔隙模型将煤体由复杂的孔裂隙系统简化为单一孔隙系统,但鉴于煤体孔隙结构的复杂性,在现实中应用该模型时会产生一定的误差;李志强等[10]根据煤粒孔隙由多尺度、大小不一的非均质多级孔隙构成,假定扩散系数D与时间也符合负指数关系,提出动扩散数学模型,将扩散模型推广到多孔隙维度;林晨等[11]的研究中扩散系数与时间关系符合幂函数关系即D(t)=atb,并对均质经典模型进行修正,取得理想描述煤粒瓦斯扩散全过程的效果。双孔隙模型分为平行孔模型和随机孔模型[12],Beamish[13]通过实验室研究表明,与单一孔隙模型相比,采用随机孔模型能更好的描述煤粒瓦斯的扩散过程,但模型考虑的因素不足,忽略了一些参数对模型的影响。刘彦伟[14]建立三重孔隙瓦斯扩散模型,分别用Dw、Dz、Dd来表示煤炭颗粒中微孔、中孔(过渡孔)、大孔的扩散系数,但三重孔隙结构非均质煤粒瓦斯扩散模型的通解仍为无穷级数解。
综上所述,构造煤的低强度、快放散等特征是影响煤与瓦斯突出的根本原因[15],在描述不同函数模型方面,关于不同函数模型在含水率煤的拟合适应性研究相对较少。本文基于瓦斯扩散试验,测定不同含水率条件下煤粒度的瓦斯解吸量,借助常扩散模型(经典扩散模型)和2种动扩散模型(指数函数扩散模型[10]、幂函数扩散模型[11])对比分析找出更适合含水煤粒解吸的扩散模型,并分析不同含水率对瓦斯扩散系数的影响,以便对煤矿瓦斯灾害防治和煤层气勘探提供参考。
1 瓦斯解吸扩散实验
1.1 煤样的采集与制备
采取平顶山八矿构造煤,变质程度属于肥煤,对煤样进行了煤的工业分析和吸附常数基本参数的测定。煤样基本参数见表1。

表1 煤样基本参数Table 1 The basic parameters of coal samples
煤样粒度为1~3 mm,为研究不同含水率对煤粒瓦斯扩散量的影响,制备了干燥煤样、原始水分煤样、湿煤样、平衡水煤样4种不同煤样进行对比。干燥煤样制作方法:将煤样置于干燥箱内,在105℃的恒温状态下干燥2 h,待煤样冷却至室温。原始水分煤样采用从现场采集的煤样。湿煤样制作方法:把制好的平衡水分煤样置于空气干燥箱内,干燥30 min左右,使煤中的水分含量处于原始水分含量与平衡水分含量之间。平衡水煤样制作方法:利用高精密天平称取样品称取65 g,将样品放入恒温箱内,箱内有过饱和硫酸钾溶液,相对湿度维持在96%~97%之间,每称重1次间隔24 h,直到相邻2次称重差值小于煤样质量的3%,表示煤样达到湿度平衡[16]。4种煤样的含水率依次为干燥煤样0.18%,原始水分1.01%,湿煤样2.88%,平衡水煤样4.98%。
1.2 实验装置
该实验装置主要由吸附—解吸单元,温度控制单元,真空抽气单元,高压充气单元及联通管路和阀门组成,如图1所示。实验温度为30℃恒温水浴,实验平衡压力为1 MPa,测定瓦斯扩散量时间为120 min。
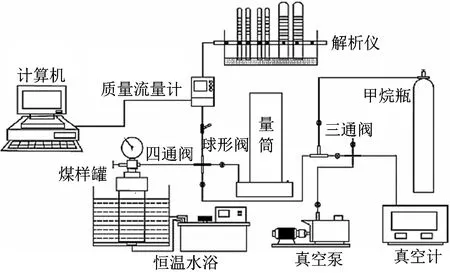
图1 瓦斯解吸实验装置Fig.1 Experimental device for methane desorption
1.3 数据处理
实测的数据还要换算成标准状态下的体积,公式如式(1)所示:
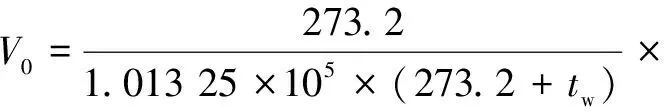
(1)
式中:V0为标准状态下的瓦斯解吸总量,cm3;V为实验条件下测得的瓦斯解吸总量,cm3;tw为量管内水温,℃;Pa为大气压力,Pa;hw为读数时量管内的水柱高度,mm;Ps为tw下饱和水蒸汽压力,Pa。
为分析水分对瓦斯解吸量的影响,刘彦伟[15]在研究煤粒瓦斯解吸规律、机理与动力学模型的过程中,在杨其銮、聂百胜等前人的研究基础上,充分考虑实验环境与煤粒吸附瓦斯的特点,认为煤粒瓦斯的极限解吸量Q∞如式(2)所示:
Q
(2)
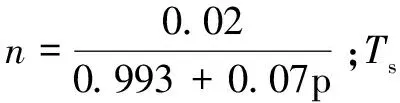
2 试验结果与分析
2.1 煤粒瓦斯解吸量的测定
利用瓦斯扩散试验装置进行了瓦斯解吸量的测定,不同含水率条件下瓦斯累计解吸量对比如图2所示。从图2可以看出,相同时段下,干燥煤样的累计瓦斯解吸量最大,随着含水率增加煤样的累计瓦斯解吸量越来越小,即含水率增加会抑制瓦斯解吸,4种不同含水率煤样的累计瓦斯解吸量曲线斜率随含水率增大而减小。
主要原因如下:扩散初期瓦斯首先从扩散阻力小的裂隙和大孔中扩散出来,其表面吸附的瓦斯气体分子瞬间快速扩散到裂隙和大孔内,随着水分的增加,煤样中的孔裂隙通道被封堵,在水分子不能进入的微孔隙内,水分子会在煤微孔隙内产生一定的蒸气压,存在一部分气体状态水分子,增大了瓦斯扩散的阻力使得单位时间内的瓦斯解吸量不断减小。
为了研究水分对煤样瓦斯解吸量的抑制程度,统计了含水煤样在时间段为0~5 min,0~20 min,0~60 min和0~120 min的累计瓦斯解吸量。其中,不同时段内瓦斯累计解吸量随水分的变化如图3所示。从图3可以看出,干燥煤样(0.18%)的5 min解吸量Q5为2.1 ml/g,原始水分煤样(1.01%)的5 min解吸量Q5为1.2 ml/g,湿煤样(2.88%)的5 min解吸量Q5为0.6 ml/g,平衡水分煤样(4.98%)的5 min解吸量Q5为0.4 ml/g;与干燥煤样相比,含水煤样累计解吸量分别降低了42.9%,71.4%和80.9%。

图2 不同含水率条件下瓦斯累计解吸量对比Fig.2 Comparison of gas desorption under different moisture conditions
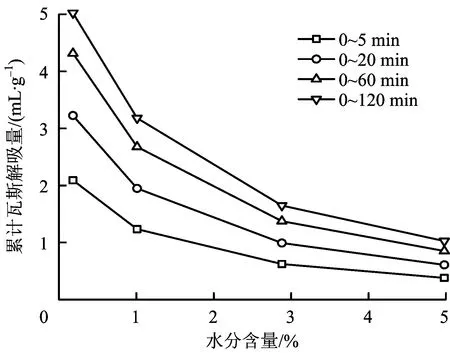
图3 不同时段内瓦斯累计解吸量随水分的变化Fig.3 Change of gas desorption with moisture in different periods
2.2 煤粒瓦斯扩散模型的比较
前人对煤粒瓦斯解吸扩散进行了大量研究,但对于能更好描述不同含水率煤样解吸过程的模型相对较少。本文针对常扩散模型和2种动扩散系数模型在含水煤样瓦斯扩散规律中的适用性进行对比,通过误差分析得出能更好描述含水煤样瓦斯扩散规律的扩散模型。3种模型模拟曲线与实验点对比如图4所示。
从图4可以看出,煤样在不同含水率条件下,经典模型在0~5 000 s相较于实验值偏小;当大于5 000 s时,相较于实验值偏大,不能准确描述瓦斯扩散过程;相较于经典模型,指数函数模型与幂函数模型有较好的吻合度,指数函数模型在瓦斯解吸初期和后期的计算值略低于实验值,中期略高于实验值;幂函数模型在瓦斯解吸初期的计算值稍高于实验值,中期和后期吻合较好。所以指数函数模型和幂函数模型模拟的扩散过程曲线与实验点有较好的吻合度,更能较准确描述瓦斯扩散全过程,较好地弥补了经典模型前期误差较大的缺点,含水率的增加并不影响模拟值与实验值的吻合度。

图4 不同含水率下3种模型模拟曲线与实验点Fig.4 Three model simulation curves and experiment points under different moisture
为直接反映出模型计算与实验测定值的差距,更准确的评价模型对含水煤粒瓦斯解吸模拟的优劣,计算煤粒扩散过程中模拟值与实验值的差值,将差值与实验值比值作为相对误差,结果如图5所示。
通过图5可知,在瓦斯解吸初期,3种模型相对误差均随时间延长而减小。对于整个瓦斯解吸扩散过程,经典模型相对误差的波动范围>指数函数模型的波动范围>幂函数模型的波动范围;相同时间内,经典模型的相对误差>指数函数模型的相对误差>幂函数模型的相对误差,即在整个瓦斯扩散过程,幂函数模型的模拟值更接近于实验值,且稳定性更好。
2.3 水分对扩散系数的影响分析
将实验测得瓦斯扩散量带入幂函数扩散模型,利用二分法可求得不同水分含量煤样的扩散系数与时间的函数式,见表2。
由表2可知,不同含水率下扩散系数随时间成幂函数递减关系即:D(t)=D0t-β,其中D0为初始扩散系数;β为衰减系数,0<β<1。将表达式用曲线图表示如图6所示。由图6可以看出,随着时间的延长,4种含水率煤样扩散系数均经历前期快速下降和后期缓慢下降2个阶段,扩散系数随着含水率的增大而减小,即扩散系数与含水率呈负相关。

表2 不同水分含量下扩散系数与时间函数关系式Table 2 Relationship between diffusion coefficient and time function under different moisture contents
扩散系数均经历前期快速下降和后期缓慢下降原因:实验煤样为构造煤,孔隙结构非常发育,扩散初期,瓦斯先从大孔和过渡孔中扩散出来,此时阻力较小,构造煤非常发育的孔隙结构为瓦斯扩散提供了扩散通道,所以扩散系数前期经历快速下降,在幂函数模型中体现为干燥煤样D0>原始水分煤样D0>湿煤样D0>平衡水煤样D0(见表2)。随着时间的延长,在浓度差的作用下瓦斯扩散逐渐过渡到微孔,扩散通道变窄使得阻力增大,所以扩散系数后期缓慢下降。
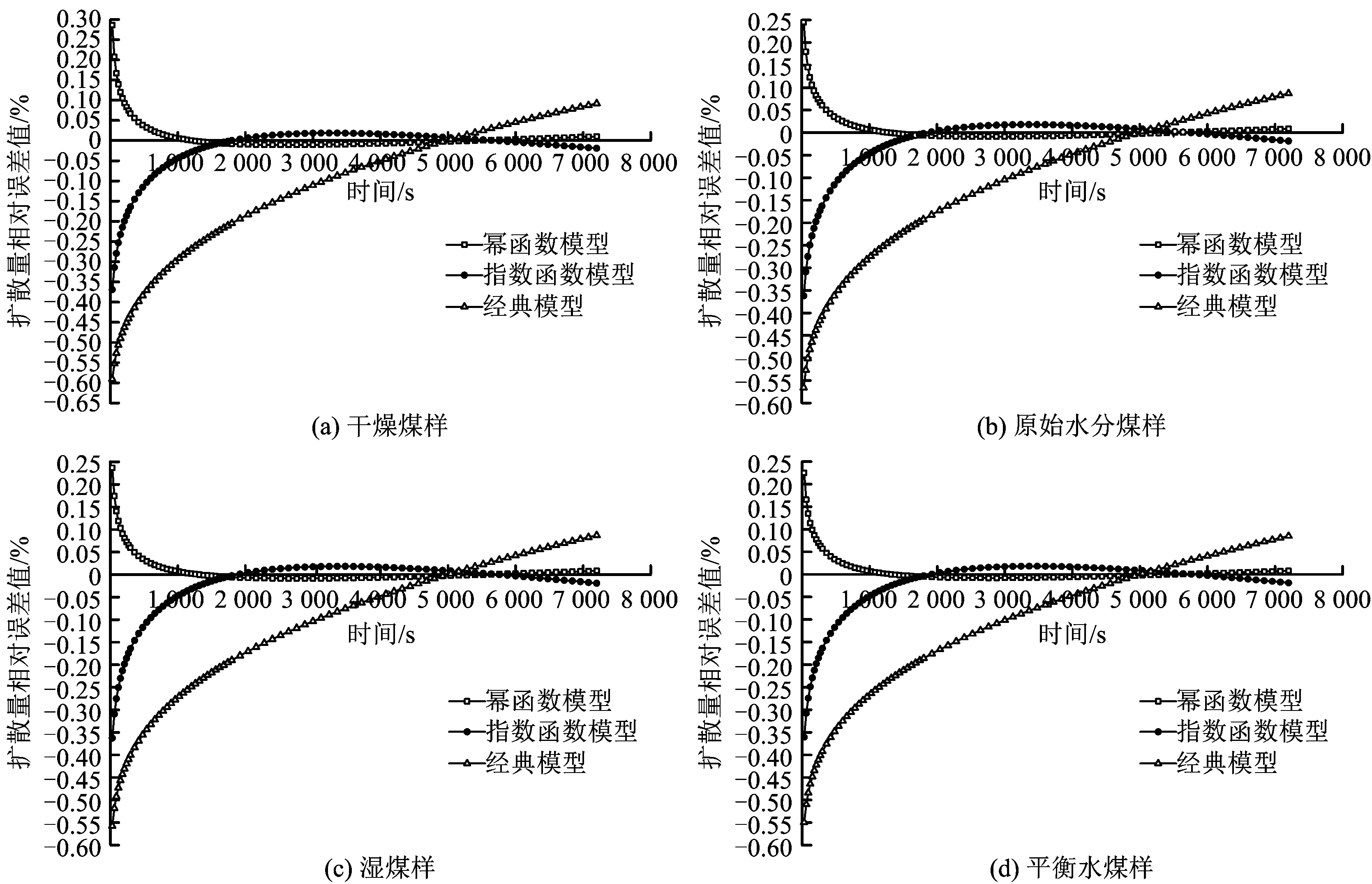
图5 不同含水率煤样扩散系数相对误差变化Fig.5 Relative error variation of diffusion coefficient of different moisture contents
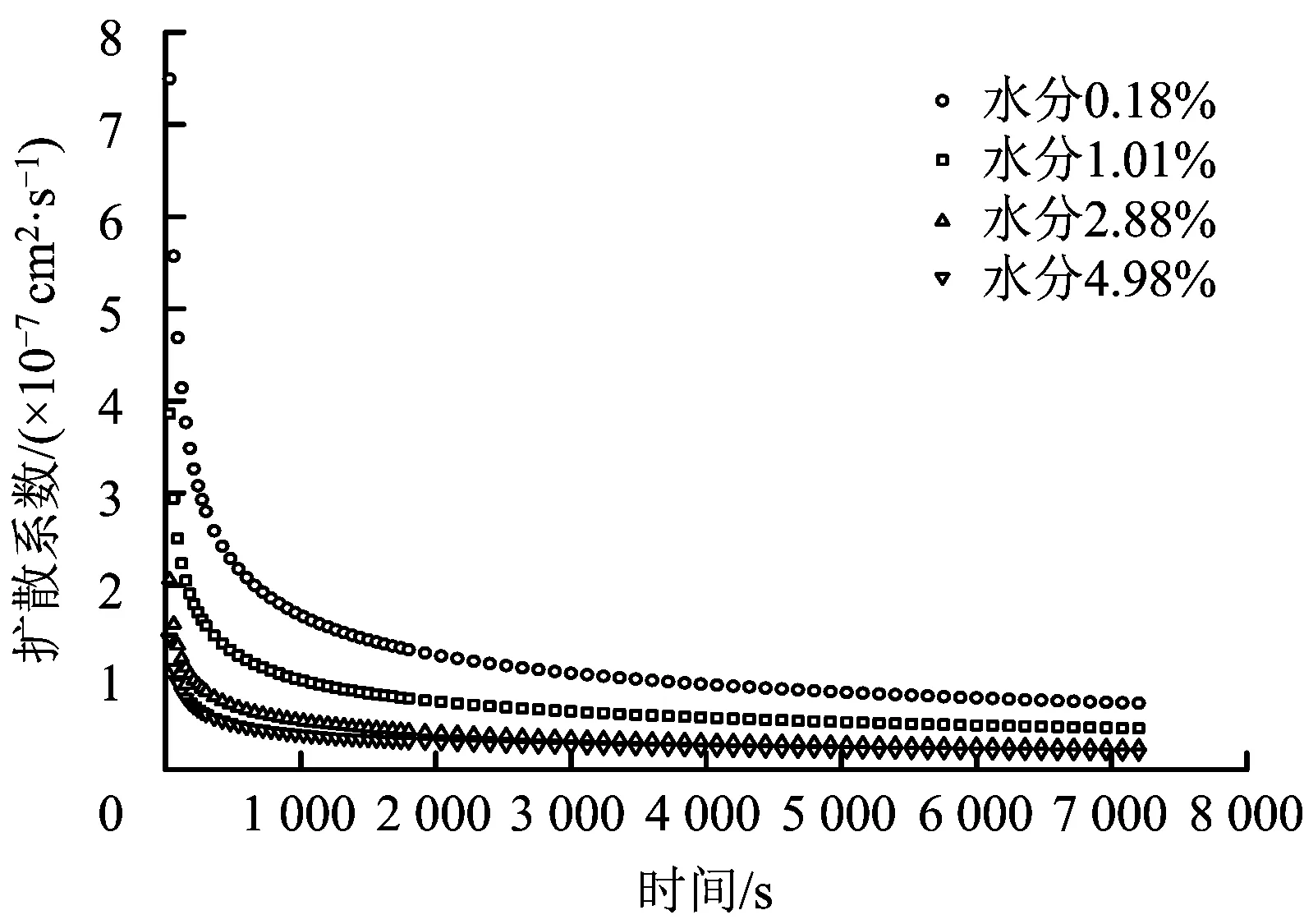
图6 不同水分瓦斯扩散系数随时间变化Fig.6 Contrast the curves of gas diffusion coefficient-time in different moisture content
扩散系数随含水率增大而减小原因:瓦斯扩散阻力在扩散初期阻力较小,后期因水分在煤孔隙内的存在堵塞了瓦斯扩散通道,使得瓦斯扩散通道变窄,瓦斯扩散需克服微孔中较大的扩散障碍使得阻力增大进而扩散系数减小。
3 结论
1)相同时段下,干燥煤样的累计瓦斯解吸量最大,随着含水率增加煤样的累计瓦斯解吸量越来越小,即含水率增加会抑制瓦斯解吸。
2)随着水分的增加,煤样中的孔裂隙通道被封堵,在水分子不能进入的微孔隙内,水分子会在煤微孔隙内产生一定的蒸气压,存在一部分气体状态水分子,增大了瓦斯扩散的阻力使得单位时间内的瓦斯解吸量不断减小。
3)通过3种扩散模型的对比,即常扩散模型和2种动扩散模型发现幂函数模型在误差大小和稳定性方面都优于其他2种模型。
4)随着时间延长,4种不同含水率煤样扩散系数随含水率的增大而减小且扩散速率趋于稳定。

