基础振动下插装阀组抗振特性分析

杨忠炯，蔡岳林，周立强，李 俊

（1.中南大学 机电工程学院，长沙 410083；2.中南大学 高性能复杂制造国家重点实验室，长沙 410083）

0 引言

插装阀具有通流能力强、结构简单、动作迅速、组件通用化、标准化程度较高等特点，因此工程实际中被广泛应用。但不同通径的插装阀所允许通过的流量均有上限值，因此常常采用多个插装阀并联成一级的方式来满足液压系统大流量要求[1]。硬岩掘进机（简称TBM）所处的工作环境及工作要求，决定了其液压系统所需工作压力高、流量大。因此插装阀组在TBM上广泛采用。例如：辽宁大伙房水库输水工程建设中应用的罗宾斯公司MB264-311型TBM其液压系统中大量采用插装阀组[2]。TBM在硬岩掘进过程中会使机器产生强烈振动[3]。插装阀组在TBM工作时，其工作性能会受到相应强振动的影响。因此需要对强振动环境下插装阀组的抗振特性做一定深入的研究。

目前关于插装阀的研究主要从单个阀体着手，并从内部结构方面进行研究，对插装阀组的研究较少。郑淑娟[4]通过计算流体力学方法对分析研究阀芯运动过程中的锥阀内流体运动状态，研究得到了锥阀流量系数，瞬态液动力在阀芯启闭过程中随锥阀流量、开口度的变化曲线。贺小峰[5]提出一种利用U型消音槽来有效减小插装阀在高压大流量环境下工作所造成的振动与噪音，并建立相应插装阀数学模型；王安麟[6]提出一种基于插装阀组启闭状态的逻辑理论，来分析插装阀组液压系统瞬时失效机理，并提出一种通过增加阀组控制腔压力的方法来提高液压集成系统稳定性。

上述各位学者的研究对于插装阀及插装阀组设计与控制具有重大意义，但均未考虑到插装阀组在基础振动下的工作特性。实际应用中的插装阀组根据先导级数的不同，分为二级插装阀组与三级插装阀组；本文针对基础振动对TBM插装阀组性能的影响，仿真研究两种插装阀组的抗振特性，分析结果将为TBM插装阀组的选型设计提供参考。

1 基础振动下插装阀组结构模型的建立

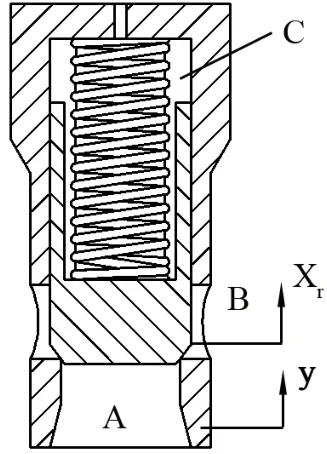
图1 振动下插装阀结构原理

从单个插装阀结构入手建立基础振动下插装阀组结构模型，如图1所示。假设插装阀在简谐运动y=Asinωt的基础振动环境中工作，在该环境下，阀芯会受到振动惯性力作用。如上图所示阀芯在进油口A、出油口B，控制腔C油压力，及控制腔中弹簧力，阀芯振动惯性力等合力作用下开启，此时阀芯相对于阀体的开启高度为Xr。以下截取TBM主机液压系统中的部分简单的插装阀组液压回路，说明二级插装阀组与三级插装阀组于基础振动下工作原理。

1.1 二级插装阀组模型

图2 二级插装阀组简易工作油路

由图2所示，该插装阀组主阀3控制腔所连先导级为电磁阀1。在电磁阀断电时，与进油口连通的控制油路通过电磁阀与插装主阀控制腔相连，在控制腔与进出油口液压合力作用下使阀关闭；在电磁阀通电后，此时与油箱相连的插装阀控制腔C内油压迅速减少，并且在系统合力作用下，主阀芯开启。

1.2 三级插装阀组模型

图3 三级插装阀组简易工作油路

由图3所示，该三级插装阀组主阀A1、A2的控制腔与一通径较小的插装阀相连。电磁阀断电后，进油口一侧油路分为两支，一支通过电磁阀与先导插装阀2的控制腔相连，在压力作用下使先导阀处于关闭状态；另一油路通过阻尼孔R1与插装阀D口相连，同时又通过单向节流阀与主阀4的控制腔相连。此时液压油路各处的压力相等，主阀处于关闭状态。在电磁阀通电时，先导阀2控制腔F与油箱相连，油压急剧下降，在系统油压作用下，先导阀芯打开。并且油路通过阻尼孔R1后压力下降，使控制腔C1、C2压力急剧下降。由于先导阀2较大的过流面积，在进口的压力油作用下，可以使控制腔C1、C2中的控制油液迅速排出推动主阀快速打开。

2 数学模型

二级插装阀组在基础振动下的数学模型较为简单，不再列写建立过程。根据以上基础振动下插装阀结构原理模型与三级插装阀组简易工作回路，通过建立基础振动下三级插装阀组的力平衡方程组与连续性方程组，建立其在基础振动下的简化数学模型，并作出以下假设：

1）视液压系统工作介质为理想流体，流体参数均为常数；

2）工作介质压力为常数，液压系统各工作元件阀腔内压力均匀分布；

3）忽略液压元件内泄露对元件工作特性的影响；

4）忽略阀芯与阀套间的摩擦力及阀芯重量的影响；

5）忽略插装阀组主阀间耦合作用，将主阀工作状态视为等效一致。

基础振动下，插装阀运动机构将在进出口油压力、液动力、弹簧力及基础振动引起的惯性力合力下在纵向作受迫振动。基于强迫振动理论[9]，简化插装阀内部结构，建立如图4所示弹簧-质量-阻尼模型。以插装阀组其中一个主阀为对象，主阀阀芯与阀体的相对位移为Xr2，先导插装阀阀芯与阀体的相对位移为Xr1；Pa1、Pb1、Pc1分别为主阀进油口A1腔，出油口B1腔，控制腔C1腔的压力，Pd、Pe、Pf分别为二级先导插装阀进油口D腔、出油口E腔、控制腔F腔的压力，Aa、Ad、Ab、Ae、Ac、Af分别为液压油路进油口A、D腔，出油口B、E腔，控制腔C、F腔的压力作用面积。

图4 基础振动下插装阀阀芯运动物理模型

插装阀组主阀芯基础振动下运动微分方程为：

其中：m2为主阀阀芯质量；Cf为油液粘性阻尼系数；k2为主阀控制腔弹簧刚度；Z20为弹簧预压缩量。

进油口流量方程为：

主阀阀口流量为：

其中：Cq为阀口流量系数；D2为主阀阀座孔直径，即α为阀口半锥角；ρ为液压油密度。

先导电磁球阀口流量为：

其中：C为流量系数，约为0.62～0.75；dp为先导电磁球阀过流孔径。

主阀控制腔流量方程为：

其中：Vc1为控制腔容积；βe为油液弹性模量；

二级先导插装阀阀芯基础振动下的运动微分方程为：

其中：m1为先导阀阀芯质量；k1为先导阀控制腔弹簧刚度；Z10为弹簧预压缩量；

先导阀阀口流量方程为：

先导阀进出口流量为：

其中：D1为阀座孔直径，即：

控制腔流量方程为：

其中：QR3=Qp；Vf为先导阀控制腔容积。

液阻R1流量方程为：

液阻R2流量方程为：

其中：dR1与dR2为阻尼孔过流孔径。

插装阀工作过程中还受到稳态液动力作用，作用力方向总是使阀芯趋于关闭。其大小与阀口过流面积及阀口压差有关，其方程为：

其中：Cw为稳态液动力计算时阀口流量系数，约为0.77～0.82，X为阀芯开启高度，∆P为插装阀进出口油液压差，α为阀口半锥角；式(1)与式(6)中Fw2与Fw1为主阀与二级先导阀阀芯所受稳态液动力。

3 仿真与分析

根据以上二级插装阀组与三级插装阀组结构模型与已建立的数学模型，建立相应液压系统AMESim仿真模型。其液压系统主要元件参数设置为：液压泵排量为300ml/r，液压泵转速为2400r/min；设定安全阀开启压力为10MPa，其他系统技术参数如表1所示；插装阀组主阀技术参数如表2所示，插装阀组主阀芯最大工作行程为14mm，主阀控制腔液阻孔径为1.2mm，弹簧刚度为50N/mm；二级先导插装阀技术参数如表3所示；阀芯最大工作行程为7mm，控制腔液阻孔径为0.8mm，弹簧刚度为10N/mm；

表1 仿真模型参数

表2 插装阀组主阀技术参数

表3 先导插装阀技术参数

3.1 基础振动下插装阀组的抗振特性分析

在基础振动（A=0.008m，f=50Hz）与无基础振动环境下，插装阀组主阀芯位移，主阀出口压力、主阀出口流量的时域变化曲线如图5至图10所示。

由图5、图6对比可知，基础振动对两种阀组主阀芯开启初期影响不大，这是由于此时插装阀主阀芯尚未达到稳态平衡，进出油口压力远大于阀芯所受弹簧力与振动引起的惯性力，阀芯因此快速上升。在主阀芯开启初期，二级插装阀组响应更快，这是由于三级插装阀组的二级先导阀的开启导致这一延迟。

伴随着先导插装阀在系统压力作用下迅速开启，三级插装阀组主阀控制腔油液通过先导插装阀迅速排出，在1.8s内达到最大开口度；二级插装阀组主阀芯开启速度低于三级插装阀组主阀芯，在3s内达到最大开口度。三级插装阀组达到阀芯最大开口度的速度较快，这是因为二级先导阀较大的过流面积，使得控制腔油液在更短的时间内排出。

最后，二级插装阀组与三级插装阀组主阀芯均在系统压力及振动引起的阀芯惯性力等合力作用下达到动态平衡。

如图5所示，取阀芯在无振动下稳态开启高度为X0，如图6所示，取振动下阀芯的稳态位移波动值为δ，定义主阀芯的波动比值为：

如图5、图6可知，在稳态下二级插装阀组主阀芯的波动比值明显高于三级插装阀组主阀芯。

图5 无基础振动下阀组主阀芯位移时域变化

图6 基础振动下阀组主阀芯位移时域变化

由图7、图8可知，插装阀组主阀在启动瞬间，出口压力会出现较大的压力超调，而后逐渐过渡到稳定状态。二级插装阀组主阀芯开启初期出口压力的最大超调量较大，三级插装阀组主阀开启更加平稳。二者调整时间基本一致，在0.6s左右达到稳态；在基础振动下，阀组的稳态出口压力会产生周期性波动，二级插装阀组稳态出口压力波动略大于三级插装阀组。

图7 二级插装阀组出口压力

图8 三级插装阀组出口压力

由图9、图10可知，阀组主阀在启动瞬间，出口流量会出现流量超调，而后逐渐过渡到稳定状态。由于三级插装阀阀组先导级开启的延迟性，三级插装阀组出口流量上升时间略大于二级插装阀组。三级插装阀组主阀出口流量波动最大超调量及调整时间较小，出口流量更为平稳。在基础振动的影响下，稳态下阀组出口流量均会产生波动，二级插装阀组稳态出口流量波动比三级插装阀组约大于23%。

图9 二级插装阀组出口流量

图10 三级插装阀组出口流量

结果表明，基础振动（A=0.008m，f=50Hz）下，二级插装阀组响应特性更好，三级插装阀组稳态特性更优；基础振动会引起阀芯的受迫振动，并引起二级插装阀组与三级插装阀组主阀芯出现位移波动，进而出现压力与流量波动。受基础振动的影响，阀芯位移，阀组出口压力，阀组出口流量最终在一个恒定值上下波动，其恒定值分别为7.31mm、7.83mm；7.74bar、7.723bar；357L/min、356.7L/min；波动幅值分别为：0.24mm、0.086mm；0.337bar、0.101bar；2.57L/min、2.02L/min；三级插装阀组在基础振动下的阀芯位移波动，出口流量波动及出口压力波动均小于二级插装阀组；取式(13)阀芯位移波动比值τ为插装阀组抗振特性主要评价指标。综上可知：三级插装阀组在基础振动（A=0.008m，f=50Hz）下的抗振特性更优。

3.2 振动参数对插装阀组抗振特性的影响分析

为确定插装阀组在不同振动参数下的抗振特性规律，以二级插装阀组与三级插装阀组主阀芯波动比值τ为评定标准。

3.2.1 基础振动幅值A的影响

图11为在基础振动（f=50Hz）下二级插装阀组与三级插装阀组主阀阀芯波动比值随振动幅值的变化曲线。

仿真结果表明，二级插装阀组与三级插装阀组主阀芯在随着基础振动的幅值增加，阀芯波动比值也随之增加；在0～5mm基础振动幅值下的阀芯波动比值均小于0.4%，二者抗振特性基本一致，受基础振动影响均较小。在振幅大于8mm后，二级插装阀组主阀芯波动，随振幅增加而明显增大，受振动影响较大。三级插装阀组主阀芯波动也随振幅增加而增大，但增幅远小于二级插装阀组，受振动影响较小，抗振特性更优。

图11 τ随振幅变化曲线

3.2.2 基础振动频率f的影响

根据越南某工地TBM掘进工作时，左右两侧撑靴振动频率实测数据显示，振动频率集中在100Hz以内。因此，仿真频率选取在0～80Hz之间。图12为在基础振动（f=0.008m）下二级插装阀组与三级插装阀组主阀阀芯波动比值随振动频率的变化曲线。

仿真结果表明：二级插装阀组与三级插装阀组随着基础振动频率的增大，阀芯波动比值也随之增加，在0～40Hz基础振动频率下的均小于0.8%，二者抗振特性基本一致，受基础振动影响较小；当振动频率大于50Hz时，二级插装阀组主阀阀芯波动比值随频率变化明显，抗振特性较差。三级插装阀组主阀芯波动也随频率增加而增大，但阀芯波动比值小于2%，受基础振动影响较小，表现出更优的抗振特性。

图12 τ随频率变化曲线

4 结论

建立基础振动下插装阀组数学模型，以插装阀组主阀芯波动比值τ为评定标准，研究分析插装阀组的抗振特性：

1）基础振动（A=0.008m，f=50Hz）下，二级插装阀组响应特性更好，三级插装阀组稳态特性更优；基础振动会引起阀芯的受迫振动，并引起二级插装阀组与三级插装阀组主阀芯出现位移波动，进而出现压力与流量波动。

2）二级插装阀组与三级插装阀组阀芯位移波动比值τ随基础振动幅值的增加而增加，随基础振动频率的增加而增加。

3）在基础振动幅值小于5mm或基础振动频率小于40Hz时，二级插装阀组与三级插装阀组抗振特性基本一致，受振动影响较小；当基础振动频率大于50Hz时，基础振动幅值大于8mm时，三级插装阀组抗振特性更优，其主阀芯波动比值基本保持在2%以下，受基础振动影响较小；二级插装阀组主阀芯波动比值增加明显，受基础振动影响较大。