俄罗斯莫斯科−喀山高铁路基地温场规律分析

刘菀茹，张玉芝，秘江辉，赵维刚，温安

俄罗斯莫斯科−喀山高铁路基地温场规律分析

刘菀茹1，张玉芝2，秘江辉2，赵维刚2，温安2

(1. 中铁二院工程集团有限责任公司，四川 成都 610031；2. 石家庄铁道大学 河北省大型结构健康诊断与控制重点实验室，河北 石家庄 050043)

针对莫斯科−喀山高铁路基典型断面，基于非稳态相变温度场数学模型，考虑气候变暖的影响，结合沿线的气候条件，对路基地温进行数值模拟计算，分析路基10 a内地温分布及变化规律。分析结果表明：路基高度越高，施工期蓄热耗散过程越长。路基深度越深，地温周期性变化幅值越小。路基横向地温存在差异，路肩位置最大冻深普遍大于线路中心处，其差值最大可达1.1 m。路基最大冻深基本在2.0~3.5 m深度范围内。路基融化过程为双向融化，开始双向融化时刻约在4月初，融化期路基顶部、路肩及坡脚位置附近存在冻土核现象，由此提出设计和施工运营过程中，需密切关注路基冻深范围内冻土的土体性质变化以及横向地温差异可能导致的横向变形。

莫斯科−喀山高铁；路基；地温分布规律；横向地温差异；最大冻深

莫喀高铁为欧亚高速运输走廊重要组成部分，线路全长770 km，设计时速400 km/h，建成后将使莫斯科−喀山14 h的铁路行程缩短为3.5 h，可积极推进新丝绸之路经济带建设。莫喀高铁具有气候极端低温(最大可达−50 ℃)、冬季漫长、有效工期短、高纬度地区修建、行车速度快、平顺性要求高等特点，如何保证其路基长期热稳定性和力学稳定性既是难点也是重点。对于路基长期稳定性分析，路基地温监测是直接、准确且有效的实时动态判断方法，我国多处寒区高铁路基已安装监测系统。牛富俊等[1−2]针对兰新客专、哈大高铁分别进行了温度、水分和变形现场监测，研究了路基温度场、水分场及变形场随季节变化特征。闫宏业等[3]在哈大高铁上布设了监测系统，研究了冻深发展规律，探究了冻结指数与冻深的关系，指出可用冻结指数计算路基冻深并给出了具体表达式。王春雷等[4]根据哈齐、大西和牡绥等线路的监测数据，分析了冻结深度和外界气温、冻胀变形之间的关系。孙宝臣等[5]在寒区高铁路基稳定性特点分析的基础上，确定了监测指标，制定了哈大高铁典型断面的监测方案，构建了适用于严寒地区高速铁路路基的多参量多测点的长期自动监测系统，并基于现场实测数据对路基稳定性进行了分析。合理的路基温度场和应力场数值模型是研究冻土区路基稳定性非常重要的方法和手段。工程实践和理论分析均表明，对于季冻区高速铁路路基而言，热稳定性仍是力学稳定性的重要影响因素[6]。温度场数值模拟是除了现场监测之外的另一种路基热稳定性分析方法。路基地温场变化规律的预测与预报可为监测系统的优化设计和路基设计、施工和运营维护提供有力参考。赖远明等[7]针对青藏铁路的传统阴阳坡路基和抛石护坡路基，利用基于伽辽金法的多孔介质对流换热有限元模型，对具有阴阳坡的抛石护坡路基和普通路基在运营24 a后的温度场进行了预报分析和比较。孙增奎等[8]考虑气候变暖影响，结合青藏铁路某试验段实际监测数据，引进“焓”来处理相变问题，利用有限元方法对多年冻土路基温度场进行了数值分析与预测。张玉芝等[9]通过现场监测数据建立的路基及周边地区土体地温估算公式，结合试验数据，考虑气候变暖的影响，采用非稳态相变温度场的数值模型对哈大高铁典型断面进行了模拟计算，研究了路基50 a内地温场的变化趋势。本文采用非稳态相变温度场数学模型，考虑气候变暖的影响，以莫喀沿线地区气候条件为依据确定基本边界条件，对莫喀高铁典型断面进行数值模拟计算，分析预测地温场的变化趋势，研究其可能对路基长期稳定性造成的影响，从而为路基防冻胀措施的设计提供 参考。

1 计算模型的建立

1.1 非稳态温度场的控制方程

由于铁路路基可认为无限长，可釆用二维模型模拟热传导过程。鉴于高铁路基级配碎石层和AB填料层的含水量通常较低，为简化模型可忽略冻融循环过程中的热量对流及水热蒸发，仅考虑多孔介质土骨架与水的导热作用和冰水相变作用。对于存在冰水相变的热传导问题来说，土体内部可分为冻结区与未冻结区，相变界面上温度随时间的变化曲线是间断的，相变界面位置的跟踪是十分困难的问题。若引入“焓”的概念来解决相变传热问题，则无须分区建立控制方程和两相界面跟踪，从而使液相区和固相区统一处理成为可能，最终使温度场更易求解。

焓随时间的变化是连续的，其表达式为[10]：

式中：为材料密度，kg/m3；df()为冻土比热，kJ/(kg·℃)；f()为凝固间隔内土体比热，kJ/(kg·℃)；du()为融土比热，kJ/(kg·℃)；为相变潜热，kJ/kg；l和s为相变温度上下限，℃；r为参考温度，℃，小于s。

引入热焓法后：

式中：为比热，kJ/(kg·℃)。

则非稳态温度场的控制方程可表示为：

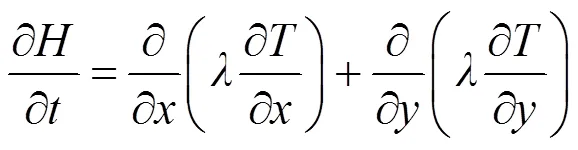
式中：为土体导热系数，J/(m·h·℃)。

试验表明，土的比热具有按各种物质成分的质量加权平均的性质，土中的气体的含量和比热均很小，可以忽略不计，则可以得到冻土和融土比热的计算式[10]：

式中：du和df分别为融土和冻土的比热，kJ/(kg·℃)；su和sf分别为融土骨架和冻土骨架的比热，kJ/(kg·℃)；i和w分别为冰和水的比热，kJ/(kg·℃)；和u分别为土体总含水量和未冻水含量。

土冻结后，并非所有液相水全部转变为固态冰，由于颗粒表面能的作用，始终保持一定数量的液态水称为未冻水，未冻水与温度有关，随温度降低而减少，升高而增大。在给定土质的情况下，不考虑外界条件以及冻融历史，可以认为未冻水含量是温度的函数，因此比热也是温度的函数。

一般热工计算中，未冻水量与温度的关系可近似按下式计算[10]：

式中：p为塑限含水量；()为温度修正系数；()为结冰率(冰重与总水重之比)；不同温度下的()和()可通过查表[10]得出。

1.2 典型断面

对于莫喀高铁路基，选取3个典型断面进行模型计算，其几何尺寸分别如图1所示。路基宽度为14.2 m，高度分别为5.3，3.4和8.7 m。其中，第1保护层为级配碎石，第2保护层、路基填土及护坡均为AB填料。级配碎石、AB填料、粉砂和粉质黏土的初始含水量分别取为10%，9%，20%和30%，其干密度分别为：1 780，2 122，1 360，1 600和 1 500 kg/m3。参考徐敩祖等[10]的研究，各土层热学物理参数如表1所示。其中，为土体密度，kg/m3；u为融土比热，kJ/(kg·℃)；为土体导热系数，J/(m·h·℃)；为土体的焓，J×106m3；d为土体比热，kJ/(kg·℃)。

单位：m

莫喀高铁沿线主要穿越温和大陆性气候，这种气候的特点是具有足够的湿润条件，温暖的夏季，寒冷多雪的冬季，冬季的天气绝大多数为多云的阴天，而且降雪量稳定。冬季(从11月中旬~3月末)的寒冷气候是适度的。由于该区域地形多为平原地带，因此主要气候参数的变化不大。由于大西洋气旋及北极气团通过该区域，因此该区域很少见强烈严寒及酷热天气，而且持续的时间也很短。以莫斯科州为例，该地区年平均气温的波动范围为6.3~5.2℃。但是，最近10年来，发现气温升高的明显趋势。从西向东的大陆性气候特点有所增长。

1.3 计算模型

选用有限元软件ANSYS进行数值模拟计算，建立的计算模型如图2所示，釆用四边形单元，级配碎石层最小单元尺寸为0.1 m，A和B填料层最小单元尺寸为0.2 m，地基层最小单元尺寸为0.5 m。

表1 各土层热学物理参数

图2 断面1计算模型

1.4 初始和边界条件的确定

对于边界条件，本文按Dirichlet边界条件进行选取。其中，路基面(EF)、天然地表(AB，IJ)及路基坡面(BE、FI)边界按式(8)进行选取，底部边界(LK)取为常数7 ℃，AL和JK视为绝热边界。在此取8月1 为起算日期，认为此时路基表面地温均达到最高值。

式中：为时间；0为年平均温度；为年振幅；为振动周期，=8 760 h；0为气候变暖引起的下附面层底地温增温率，0=0.04/8 760 ℃/h[12]。

根据莫喀高铁沿线气象资料及附面层原理[13]，不同断面的温度边界条件按表进行选取。

1.5 求解方法

在进行路基温度场预测瞬态分析之前，除了选定边界条件外还需确定其初始温度场。初始温度场的确定一般有2种思路：利用现场监测资料进行赋值；利用已有统计资料进行瞬态计算，求得稳定初始温度场。本文由于没有现场监测资料，故采用瞬态计算的方式来求得初始温度场。

表2 温度边界条件

初始温度场的求解。求解初始温度场时，将地基深度范围内地温梯度设置为0.04 ℃/m(通过稳态分析实现)，下边界温度设置为7 ℃，天然地基两侧设置为绝热边界，天然地基面(AJ)的温度荷载按式(8)进行设置；设置最小时间子步为12 h，最大为24 h，打开自动时间步长，通过迭代次数变化使得计算软件自主选择时间步长进而实现地基温度场瞬态分析。经对比分析得10 a后地基温度场基本处于稳定状态，选取此时的温度场为初始地基温度场。初始路基温度场的取值与初始地基温度场的上边界温度保持一致。

温度场的预测分析。利用求得的初始温度场与式(8)表示的边界条件进行瞬态求解。设置时间总步长为10 a，每一子步长为24 h，共计3 650步。涉及相变的材料，均输入热焓。

2 计算结果分析与讨论

2.1 路基温度场稳定过程

路基断面由于高度较高，土体的累积热阻较大，而施工完成日期气温接近年气温最高值，储蓄了较多的热能，在路基建成后的一定周期内，路基及下卧土层向边坡外土体散热。各断面构筑完成后10 a内典型位置处地温时程曲线如图3所示。由于几何模型与边界条件均对称，故在分析不同位置点的温度时程变化时仅以左半侧模型为例来进行 说明。

通过对比图3各断面典型位置地温时程曲线可知，随着路基高度的增加，路基及其下卧土层蓄积热量的耗散过程越长。其中，断面1、断面2和断面3的路基及其下卧土层蓄积的热量分别在路基修筑4，3和6 a之后完成散热的过程，新的热力平衡状态基本形成。此后不同位置的地温逐渐升温主要是由于边界条件中考虑气候变暖的影响。对比分析图3(a)与图3(b)可知，各断面相同地基深度(1.5 m)位置处，左路肩温度场最终稳定值均大于线路中心处。

(a) 左路肩地基以下1.5 m温度时程曲线；(b) 线路中心地基以下1.5 m温度时程曲线

为探究各断面蓄积热量的具体耗散过程，各断面不同位置时程曲线对比图如图4~6所示。

由图4可知，路基构建初期，土层蓄积热量的耗散较为迅速，路基深度越深热量耗散过程越明显，热量耗散完成(4 a)后，路基地温随气候变化呈周期性稳定状态发展。无论是热量耗散过程中还是热量耗散完成后，相同深度处，左路肩地温变化幅值均大于线路中心处。热量耗散完成后，地温变化幅值随着路基深度的增加而减小，路基顶面和原地面线最大幅值差可达15 ℃(路基高5.3 m)。断面2和断面3温度场变化规律与断面1类似，如图5和图6所示。

对比图3~6可知，路基高度越高(3.4，5.3，8.9 m)，路基及其下卧土层蓄热耗散过程越长(3，4和6 a)。路基深度越深，热量耗散完成后地温变化幅值越小。当路基深度达到一定深度后(大约5.0 m深)其地温变化较小，无论春、冬季其地温均为正温(4℃以上)，温度变化幅值较小(温差小于5 ℃)。

(a) 左路肩不同深度位置地温时程曲线；(b) 线路中心不同深度位置地温时程曲线

(a) 左路肩不同深度位置时程曲线；(b) 线路中心不同深度位置点时程曲线

(a) 左路肩不同深度位置时程曲线；(b) 线路中心不同深度位置时程曲线

2.2 典型时刻温度场分布规律

一般来说，路基及边坡温度场分布为各断面地温分析的重点，现截取坡脚外沿5 m，自然地面以下10 m区域进行冻深分析，各断面最大冻深时刻温度场分布如图7所示。图中水平位置正、负号分别代表路基右、左侧，竖向位置正、负号分别代表原地面以上、以下。

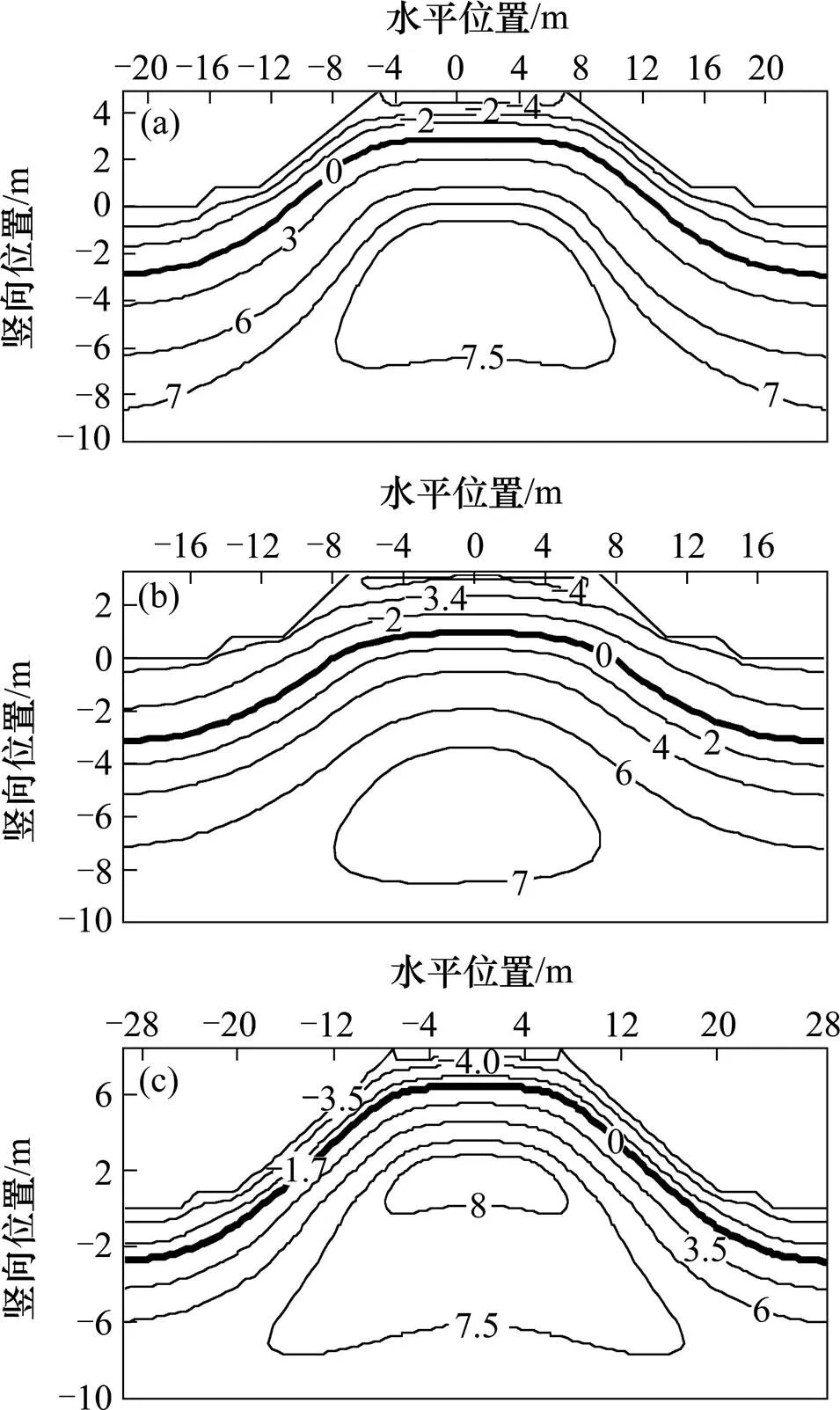
单位：℃

由图7可知，路基高度越高，路基顶面与原地面线温度差越大，地基内部温度梯度越小，断面温度梯度较大位置集中在路基6~7 m深度范围内。路基高度越高，最大冻深时刻越早，但基本都在3月中下旬冻深达到最大。各断面路肩最大冻深均大于线路中心，具体数值如表3所示。

由表3可知，3个路基断面最大冻深基本在2.0~3.5 m深度范围内。路肩位置最大冻深普遍高于线路中心，这是由于路肩部位毗邻边坡，直接暴露于外界气候造成的，同时应注意地温差异可能导致的横向不均匀变形。在路基方案及相应监测方案设计过程中，应注意实际冻深的范围，将冻深范围内填料换填为微冻胀填料，布设地温监测元件时，应综合考虑路基高度，确定监测范围。

各断面开始融化时刻温度分布图如图8所示。

表3 各断面最大冻深

单位：℃

由图8可知，由于路基冻深范围以外的土体始终处于正温，到达最大冻深后冷量无法向下传递。因此春季来临时，随着路基表面温度逐渐升高，路基的融化过程表现为自上而下和自下而上同时进行的双向融化，开始双向融化时刻约在4月初，融化持续时间较短，约为20 d左右。双向融化期路基内部有冻土核存在，其主要分布在路基顶部、路肩及坡脚位置附近。在路基方案及相应监测方案设计过程中时，应重点关注该时期、该区域土体性质变化，以防止路基产生过大冻胀变形。

3 结论

1) 路基的修筑会改变周边区域的地温分布，路基及其下卧土层蓄热耗散过程与路基几何尺寸(尤其是路基高度)密切相关。路基高度越高(3.4，5.3和8.9 m)，蓄热耗散过程越长(3，4和6 a)。路基深度越深，其地温周期性变化幅值越小(温度变化幅值小于5 ℃)，而且无论春、冬季其地温均为正值(4 ℃以上)。

2) 路基横向地温存在差异，路肩位置最大冻深普遍大于线路中心处，其差值最大可达1.1 m，路基最大冻深基本在2~3.5 m深度范围内。路基高度越高，最大冻深时刻越早，基本在3月中下旬冻深达到最大。

3) 路基冻结过程为单向冻结，融化过程为双向融化，开始双向融化时刻约在4月初。双向融化期路基内部有冻土核存在，其主要分布在路基顶部、路肩及坡脚位置附近。

4) 设计和施工运营中的监测均应密切关注冻深范围内土体稳定性，以免产生过大路基变形，影响行车安全运行。同时关注路基横向地温差异可能引起的不均匀变形。

[1] 牛富俊, 林战举, 吴旭阳, 等. 兰新客运专线浩门区间路基温度、水分及冻胀变形特征[J]. 冰川冻土, 2016, 38(4): 1074−1082. NIU Fujun, LIN Zhanju, WU Xuyang, et al. Characteristics of subgrade’s temperature，moisture and frost heave deformation in Haomen, passenger railway line from Lanzhou to Xinjiang[J]. Journal of Glaciology and Geocryology, 2016, 38(4): 1074−1082.

[2] NIU F, LI A, LUO J, et al. Soil moisture, ground temperatures, and deformation of a high-speed railway embankment in Northeast China[J]. Cold Regions Science & Technology, 2016, 133: 7−14.

[3] 闫宏业, 蔡德钩, 杨国涛, 等. 高寒地区高速铁路路基冻深试验研究[J]. 中国铁道科学, 2015, 36(3): 1−6. YAN Hongye, CAI Degou, YANG Guotao, et al. Experimental study on permafrost of high-speed railway subgrade in alpine region[J]. China Railway Science, 2015, 36(3): 1−6.

[4] 王春雷, 张戎垦, 赵晓萌, 等. 季节冻土区高速铁路路基冻胀监测系统及冻胀规律研究[J]. 冰川冻土, 2014, 36(4): 962−968. WANG Chunlei, ZHANG Rongken, ZHAO Xiaomeng, et al. Frost heaving monitoring system and frost heaving rules for the high-speed railway embankment in the seasonally frozen soil regions[J]. Journal of Glaciology and Geocryology, 2014, 36(4): 962−968.

[5] 孙宝臣, 张玉芝, 李剑芝, 等. 严寒地区高速铁路路基稳定性长期监测研究[J]. 铁道工程学报, 2015, 32(1): 22−26. SUN Baochen, ZHANG Yuzhi, LI Jianzhi, et al. Long-term monitoring of high-speed railway roadbed stability in cold regions[J]. Journal of Railway Engineering Society, 2015, 32(1): 22−26.

[6] 张玉芝. 深季节性冻土地区高速铁路路基稳定性研究 [D]. 北京: 北京交通大学, 2015. ZHANG Yuzhi. Study on the stability of high-speed railway roadbed in deep seasonally frozen region[D]. Beijing: Beijing Jiaotong University, 2015.

[7] 赖远明, 张鲁新, 张淑娟, 等. 利用抛石护坡调节冻土路基阴阳坡的温度分布[J]. 岩石力学与工程学报, 2004, 23(24): 4212−4220. LAI Yuanming, ZHANG Luxin, ZHANG Shujuan, et al. Adjusting temperature distribution under the north and south slopes of roadbed by the ripped-rock reventment in permafrost regions[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(24): 4212−4220.

[8] 孙增奎, 王连俊, 白明洲, 等. 青藏铁路多年冻土路堤温度场的有限元分析[J]. 岩石力学与工程学报, 2004, 23(20): 3454−3459. SUN Zengkui, WANG Lianjun, BAI Mingzhou, et al. Finite element analysis on temperature field of Qing- Tibet railway embankment on permafrost[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(20): 3454−3459.

[9] 张玉芝, 杜彦良, 孙宝臣. 季节性冻土地区高速铁路路基地温分布规律研究[J]. 岩石力学与工程学报, 2014, 33(6): 1286−1296. ZHANG Yuzhi, DU Yanliang, SUN Baocheng. Temperature distribution in roadbed of high-speed railway in seasonally frozen regions[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(6): 1286− 1296.

[10] 徐敩祖, 王家澄, 张立新. 冻土物理学[M]. 2版. 北京:科学出版社, 2010. XU Xiaozu, WANG Jiacheng, ZHANG Lixin. Physics of frozen soils[M]. 2nd ed. Beijing: Science Press, 2010.

[11] 黄厚诚, 王秋良. 热传导问题的有限元分析[M]. 北京: 科学出版社, 2011. HUANG Houcheng, WANG Qiuliang. Finite element analysis of heat condution problem[M]. Beijing: Science Press, 2011.

[12] Romanovsky V E, Drozdov D S, Oberman N G, et al. Thermal state of permafrost in Russia[J]. Permafrost Periglacial Processes, 2010, 21(2): 136−155.

[13] 朱林楠. 高原冻土区不同下垫面的附面层研究[J]. 冰川冻土, 1988, 10(1): 8−14. ZHU Linnan. Study of the adherent layer on different types of ground in permafrost region on the Qinghai- Xizang Plateau[J]. Journal of Glaciology and Geocryology, 1988, 10(1): 8−14.

(编辑 阳丽霞)

Temperature distribution of Moscow-Kazan high-speed railway roadbed in Russia

LIU Wanru1, ZHANG Yuzhi2, BEI Jianghui2, ZHAO Weigang2, WEN An2

(1. China Railway Eryuan Engineering Group Co., Ltd., Chengdu 610031, China; 2. Key Laboratory of Large Structure Health Monitoring and Control, Shijiazhuang Tiedao University, Shijiazhuang 050043, China)

Considering the climate warming and the atmosphere conditions along the line, the mathematic calculations of unsteady phase transition temperature field of three typical sections of the Moscow-Kazan HSR roadbed were put forward to analyze the temperature distribution and variation rules in the next 10years. The results show: The higher the height of the roadbed is, the longer the heat dissipation process is. The deeper the depth of the roadbed is, the smaller the temperature amplitude of the periodic change is. There exists transverse differences. The maximum frost depths of the shoulders are greater than the center of the roadbed with the value up to 1.1 m. The maximum frost depths are in the range of 2.0~3.5 m. The melting process of the roadbed is bidirectional, and it begins on the early April. There is a phenomenon of frozen nucleus near the top of the roadbed, the shoulder and the toe position. Then the conclusions are proposed, the soil properties in the range of frost depths and the possible transverse uneven deformation resulted from the transverse differences should be paid more attention to.

Moscow-Kazan high-speed railway; roadbed; temperature distribution; transverse temperature difference; maximum frost depth

10.19713/j.cnki.43−1423/u.2018.08.004

U213

A

1672 − 7029(2018)08 − 1928 − 09

2017−06−26

河北省自然科学基金资助项目(E2017210110)；中国铁路总公司科技研究开发计划课题(2016G002-A)；河北省高等学校科学技术研究项目(ZD2016143)；中国中铁股份有限公司重大专项课题(2016-重大专项-01)

张玉芝(1979–)，女，河北定州人，讲师，博士，从事寒区高速铁路路基工程研究；E−mail：zhangyuzhi@stdu.edu.cn