基于渐进损伤的纤维全缠绕铝内胆气瓶自紧工艺

章 昕 赵建平

(南京工业大学机械与动力工程学院，南京 211816)

0 引言

复合材料压力容器在工业生产中有着重要的应用，它综合了传统压力容器和复合材料的优势，大大提升了压力容器的使用范围、效率和寿命[1]。国内外对于复合材料压力容器失效的分析和性能的预测主要方法为有限元软件分析与试验结果相对照，来验证分析结果的可靠性。纤维缠绕复合材料压力容器，由于其复合材料层的纤维缠绕结构的特殊性，在承载的过程中其应力是渐进变化的，材料性能也是逐渐退化的，因此需要运用渐进损伤的分析方法对复合材料层进行分析[2]。在诸多的复合材料压力容器中，复合材料气瓶使用最为广泛。纤维缠绕气瓶又因其封头处缠绕方法的特殊性，要利用经典网格理论对气瓶封头处的几何方程进行分析[3]。

通常在气瓶水压试验之前，需要进行一次自紧工艺循环，自紧力的大小往往高于水压试验压力，使得气瓶承载自紧力时内衬层发生屈服，自紧力卸载后内衬层存在一定的残余压应力，气瓶再承载时抵消一部分应力，提高气瓶承载力和疲劳寿命，同时优化内衬层和复合材料层之间的应力分布[4-5]。

自紧工艺对气瓶是必不可少的一道工艺，本文基于复合材料的渐进损伤的分析方法，从理论和数值模拟的角度分析了复合材料气瓶自紧工艺的原理以及必要性，确定了合理自紧力的范围。

1 复合材料的渐进失效分析

1.1 复合材料失效准则和材料退化模式

复合材料的失效准则依据不同的分类标准可以分为很多类。依据在失效分析过程中有无失效模式可以分为：模式相关准则和模式无关准则。最大应力准则、最大应变准则、蔡-希尔(Tasi-Hill)强度准则、蔡-吴(Tasi-Wu)张量强度准则均属于模式无关的失效准则[2]。

三维Hashin失效准则属于模式相关的失效准则。具体内容为[6-8]：

(1)纤维拉伸失效(σ11>0)：

(1)

(2)纤维压缩失效(σ11<0)：

(2)

(3)基体拉伸失效(σ22>0)：

(3)

(4)基体压缩失效(σ22<0)：

(4)

(5)基体拉伸剪切失效(σ11<0)：

(5)

(6)拉伸分层失效(σ33>0)：

(6)

(7)压缩分层失效(σ33<0)：

(7)

式中,7个失效判据σ11，σ22，σ33，τ12，τ13，τ23分别表示单层板中的6个应力分量；XT，XC，YT，YC，S12，S13，S23，ZT，ZC分别表示单层板材料性能的9个常数。

复合材料层局部放大可以看作是层合板结构[2]。层合板结构在承载的过程中，某一单层板发生损伤时，层合板不会直接失去承载能力，而是通过刚度矩阵的折减来实现材料性能退化的过程[9]。基于Chang和Camanho材料刚度折减方案，提出刚度折减方案，具体内容见表1。其中，当折减系数为1时表示该材料参数没有发生折减。

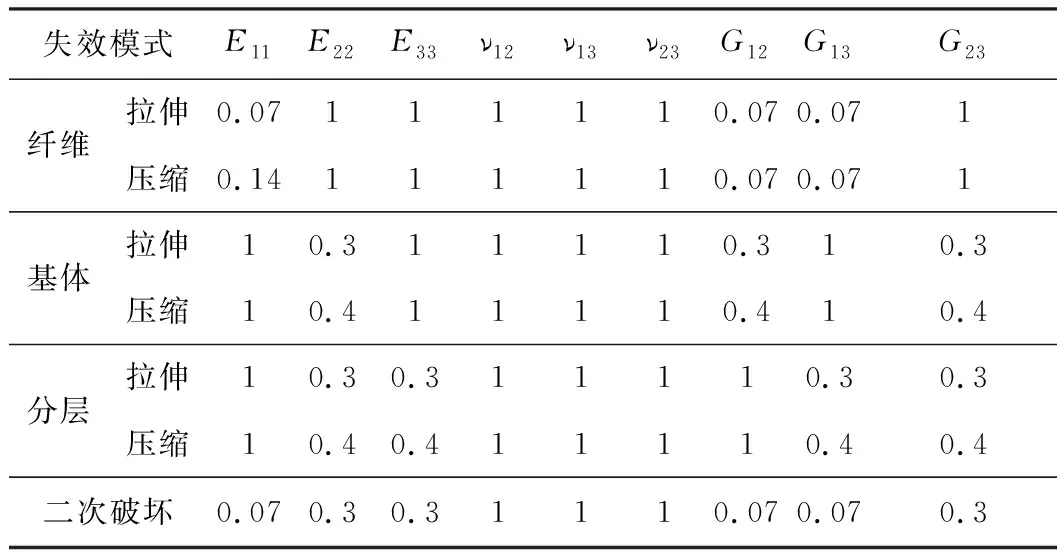
表1 材料性能参数退化表

1.2 VUMAT子程序编写及验证

参照复合材料渐进损伤分析的理论过程，主要包括应力应变的计算、失效模式的判断、失效评定、载荷的增加、刚度折减和最终失效等内容。逻辑图如图1所示。

根据文献[10]，选用如图2所示的层合板模型来验证子程序的正确性。层合板结构中间开孔，开孔直径D=15 mm，长度L=250 mm，宽度W=25 mm，厚度t=1.68 mm。层合板左端面施加全约束，层合板右侧施加位移约束。

模型计算可得，层合板的失效载荷为1.14 kN，在该力的作用下层合板沿纤维方向的应力S11的值为310.4 MPa，而文献中试验所得的数据为290.0 MPa，两者误差为7.03%，说明子程序的正确性。

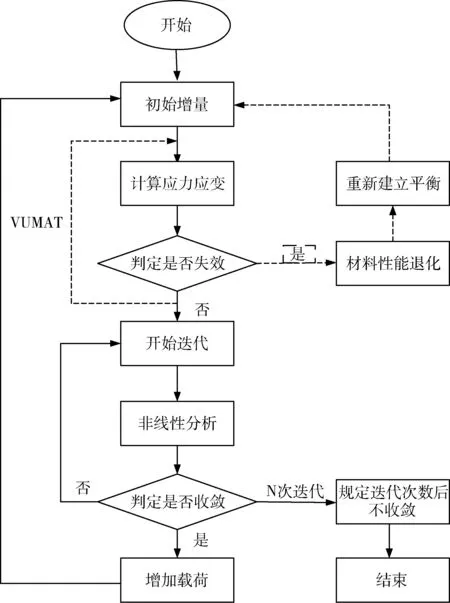
图1 子程序编写逻辑图Fig.1 Logic diagram of the VUMAT program

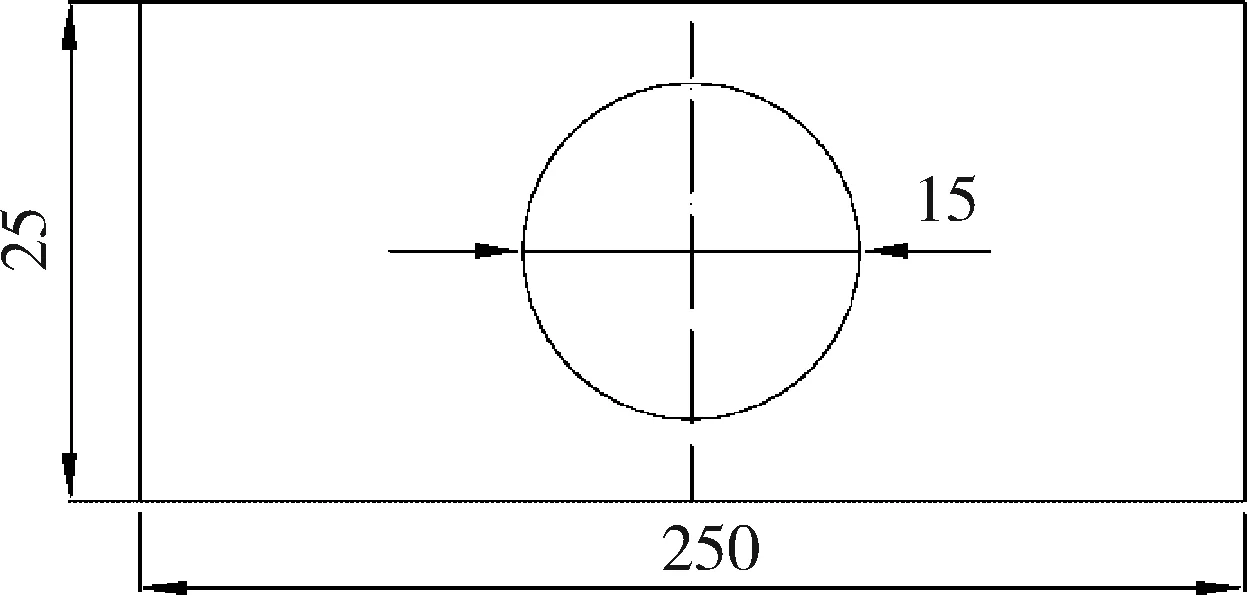
图2 含开孔结构复合材料层合板Fig.2 Composite laminated plates with a center hole curve of layup under tensile loads hole

2 气瓶的渐进损伤分析

2.1 气瓶的几何模型

本文分析的对象为纤维全缠绕铝内衬气瓶，采用ABAQUS有限元软件建立模型并运用VUMAT子程序分析计算。气瓶内衬的内径为95 mm，壁厚为2.5 mm，筒身段的缠绕方式为环向和螺旋缠绕组合的方式，缠绕顺序为[90°2/14°2/90°2/14°2/90°2/14°2]，其中，环向缠绕层的纤维厚度为0.16 mm，螺旋缠绕层的纤维厚度为0.18 mm，封头段只存在螺旋缠绕。封头段纤维缠绕厚度是随着平行圆直径的变化而变化，按照式(8)(9)进行计算[11]，计算结果见表2。由于

气瓶结构的对称性和受力的对称性，建立实际结构环向的1/2模型进行分析和计算。

α=arcsin (r/R)

(8)

(9)

式中,α为纤维缠绕角；r为极孔半径；R为纤维缠绕处平行圆半径；R0为内衬筒身段半径；tf为缠绕层厚度。

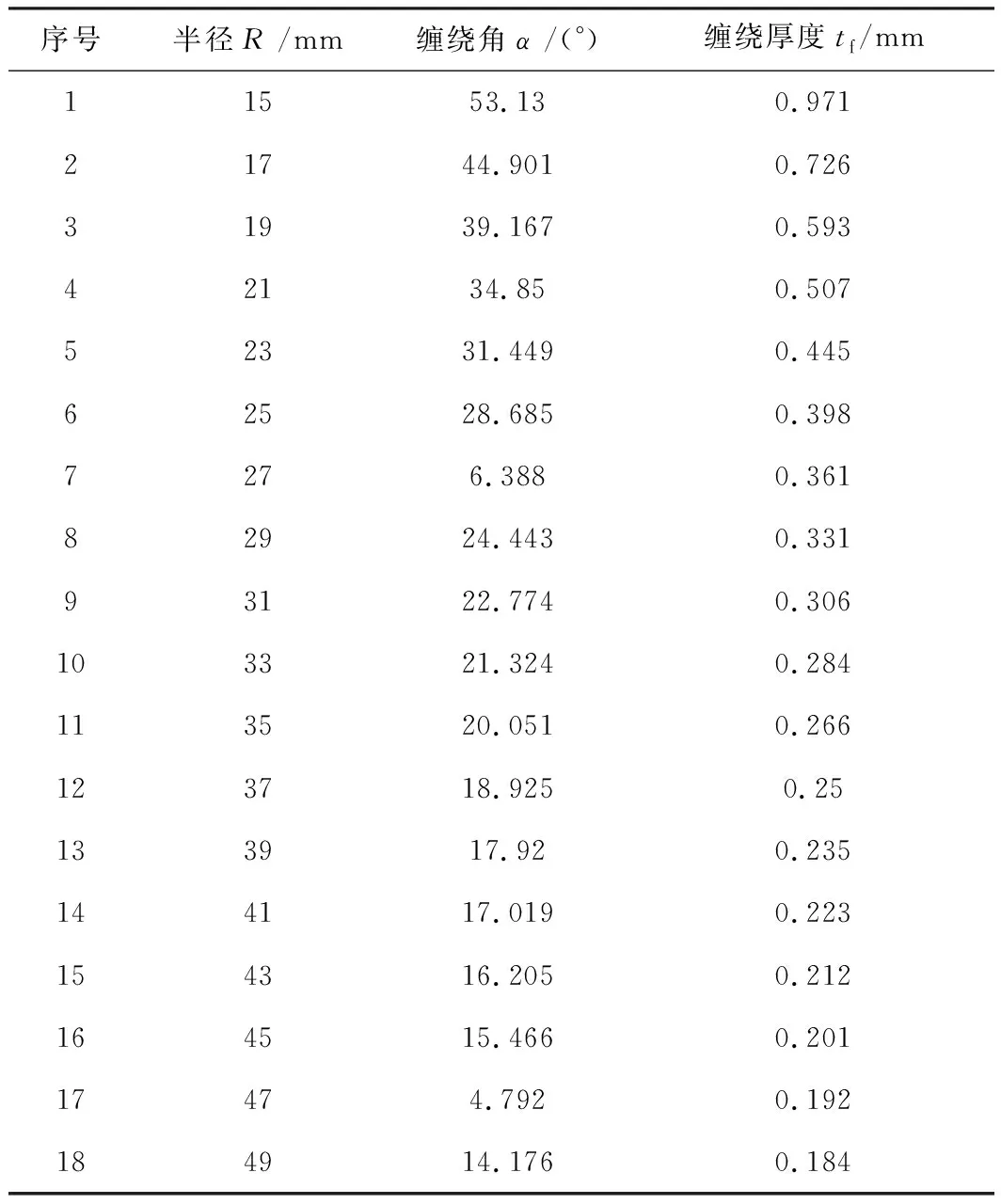
表2 封头纤维缠绕角和纤维缠绕厚度随平行圆半径变化Tab.2 Wound angle and real thickness of the composite on the head according to the radius of the parallel circle

气瓶内衬材料为铝合金6061Al-T6，材料性能参数见表3。纤维缠绕层采用T700型碳纤维为增强材料，环氧树脂为基体材料，材料参数见表4。依据对称性，在轴向对称面施加对称约束，在内衬层和纤维缠绕层之间施加绑定约束。

表3 铝合金6061Al-T6力学性能[12]

表4 复合材料T-700/环氧树脂力学性能[13]

2.2 复合材料渐进损伤分析

从16 MPa开始逐渐增加气瓶内压直至爆破，探究气瓶的应力变化和复合材料的损伤累积和发展的过程。

2.2.1复合材料层损伤过程

(1)基体拉伸损伤，图3为基体拉伸损伤的发展过程，如图所示基体拉伸损伤发生较早，内压为25 MPa时萌发，由封头开始向筒体发展。螺旋缠绕层最先发生，由复合材料层外侧向内侧发展。内压为34 MPa时，筒体开始大面积出现失效单元，40 MPa时，发展更加迅速。

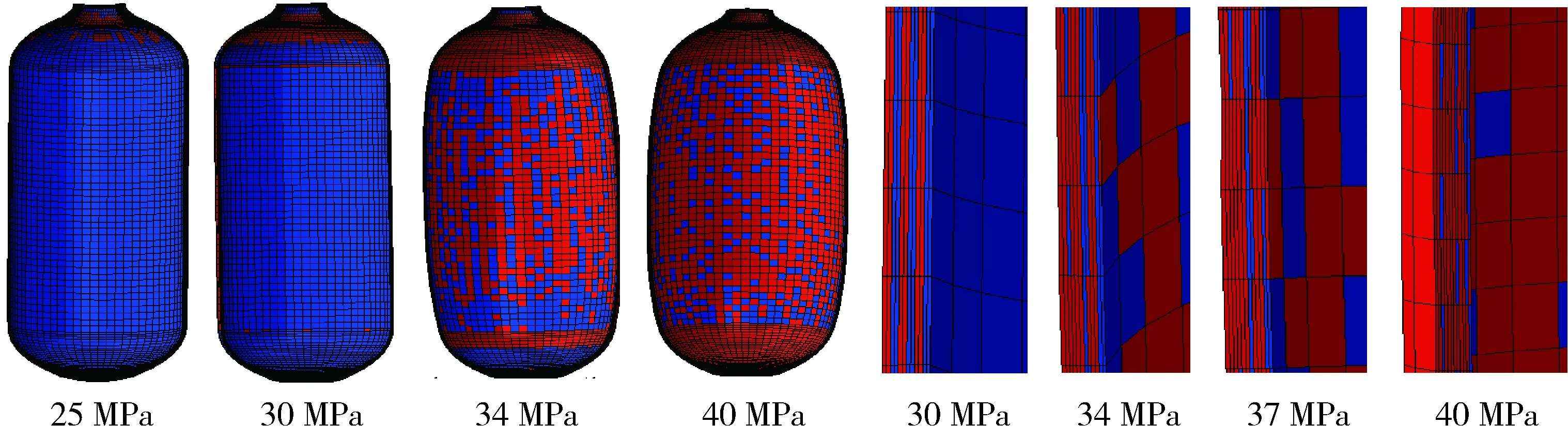
图3 复合材料层基体拉伸损伤随内压的发展Fig.3 Development of matrix tensile damage of composite under increasing internal pressure

(2)基体压缩失效，图4为基体压缩损伤的发展过程，基体压缩损伤从内压为34 MPa开始，由筒体中部开始向两端发展，螺旋缠绕层最先发生，由复合材料层内侧向外侧发展。

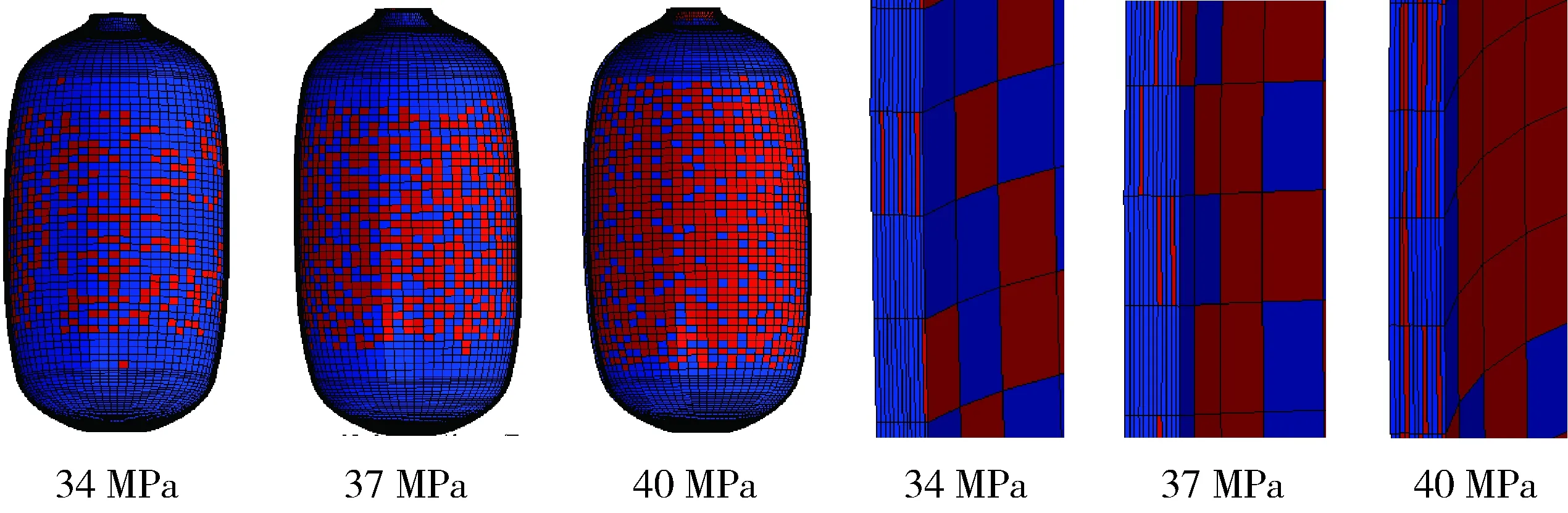
图4 复合材料层基体压缩损伤随内压的发展Fig. 4 Development of matrix compression damage of composite under increasing internal pressure

(3)拉伸分层失效，图5为拉伸分层损伤的发展过程，拉伸分层损伤从内压为30 MPa开始，由筒体底部开始向顶端发展，由复合材料内侧向外侧发展。

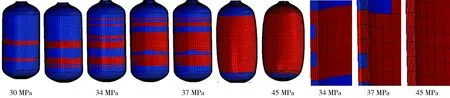
图5 复合材料层拉伸分层损伤随内压的发展Fig.5 Development of tensile delamination damage of composite under increasing internal pressure

(4)纤维拉伸失效，图6为纤维拉伸损伤的发展过程，纤维拉伸损伤从内压为34 MPa开始，由筒体中部向两端发展，由内侧向外侧发展，当内压为40 MPa时开始向封头发展。

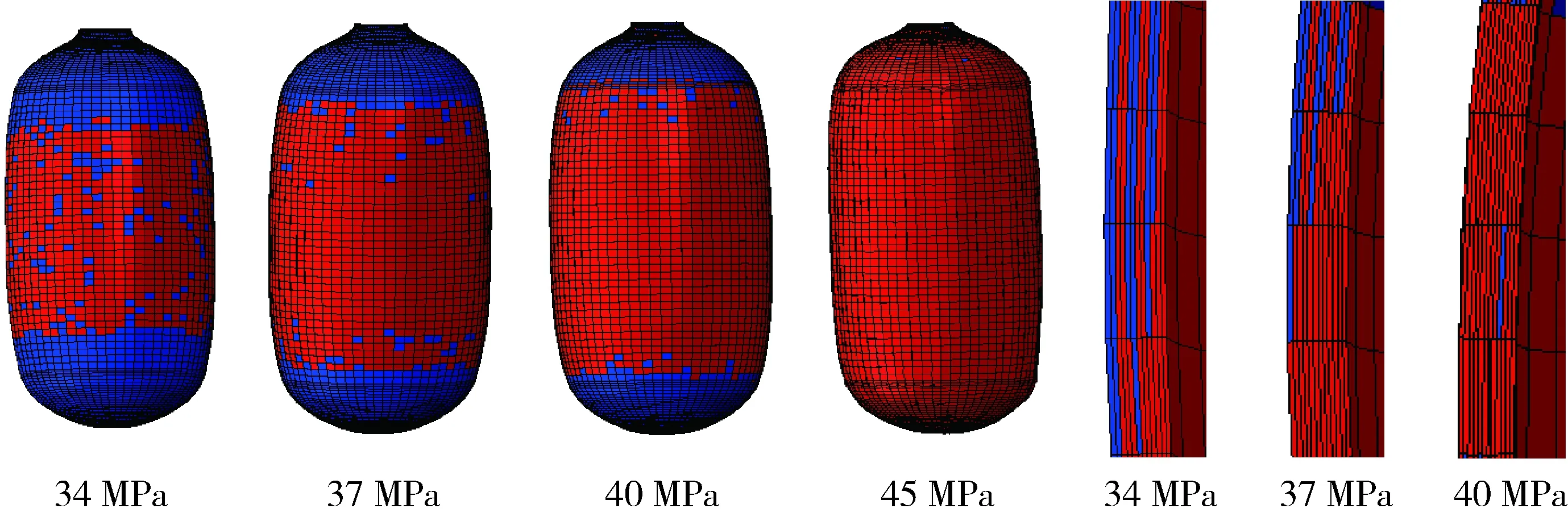
图6 复合材料层纤维拉伸损伤随内压的发展Fig.6 Development of fiber tensile damage of composite under increasing internal pressure

综上，复合材料层损伤发生的顺序或可能性：基体拉伸>拉伸分层>纤维拉伸/基体压缩。且损伤大都从螺旋缠绕层开始。除基体拉伸损伤由封头向筒体发展，由复合材料外层向内层发展，其余损伤大都从筒体中部向两端发展，由内层向外层发展。对于算例模型，当内压达到34 MPa时，筒体开始出现多种模式的损伤，因此从减少复合材料损伤的角度，自紧力应小于34 MPa。

2.2.2气瓶的应力分析

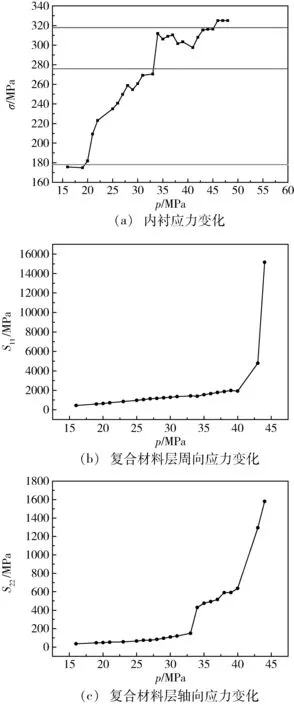
图7 复合材料气瓶应力随内压的变化Fig.7 Stress of composite cylinder under increasing internal pressure

气瓶内衬应力变化和复合材料层周向及轴向应力变化见图7。由图7(a)可知，内衬应力随内压的增加逐渐变大，内压为34 MPa时内衬应力开始大幅增加，在44 MPa时应力达到拉伸强度318 MPa。由图7(b)可知，当内压达到40 MPa时，复合材料层周向应力大幅增加，到44 MPa时应力激增，说明44 MPa为爆破压力。由图7(c)可知，内压分别在34和40 MPa时，复合材料层轴向应力大幅增大。因此从应力变化的稳定性角度，自紧力应小于34 MPa。

由DOT—CFFC 2007标准[14]可知，工作压力下的复合材料气瓶的内衬上任一点的最大拉伸应力不得超过材料屈服强度的60%，即276×60%=178 MPa，由图7(a)可知，气瓶的最大工作压力为20 MPa。假设筒身达到爆破压力pb，且认为壳体爆破时纵向和环向纤维抗力都达到发挥强度即Xt、Yt，则纤维环向总厚度为[15]：

(10)

式中，R为筒体半径，pb为爆破压力，α为螺旋层角度，tfθ为环向层总厚度。

将爆破压力为44 MPa代入式(10)，可得纤维环向层总厚度为1.1 mm，与实际环向层总厚度0.96 mm，误差为14.5%，在工程允许的误差范围内，说明了有限元结果的正确性。

3 气瓶的自紧工艺

在气瓶水压试验之前，进行一次自紧工艺，自紧力的大小往往高于水压试验压力，使得自紧时内衬层发生屈服，自紧力卸载后内衬层存在一定的残余压应力，气瓶再承载时可抵消一部分应力，优化内衬层和复合材料层之间的应力分布。ASME规定，水压试验压力：

pT=1.3pw(σ/σt)

(11)

式中，pT为水压试验压力，pw为最大允许工作压力，(σ/σt)为应力修正系数。

应力修正系数取1，由气瓶的应力分析可知pw为20 MPa，所以pT为26 MPa。因此自紧力取值应大于26 MPa，结合复合材料渐进损伤分析，自紧力应小于34 MPa。分别取工作压力为20、25 MPa，取自紧力范围为28～39 MPa进行试算，气瓶的应力变化见图8～图10。特别的，图中横线表示25、20 MPa工作压力下未经自紧工艺处理的气瓶的应力水平。

由图8可知，随着自紧力的增加，工作压力下气瓶内衬的应力先减小后增大。当自紧力为30～33 MPa时，内衬应力低于未经自紧的气瓶内衬的应力，当自紧力为30 MPa时，内衬应力达到最低，即自紧水平最好。

由图9和10可知，当自紧力为30～33 MPa时，经过自紧工艺的气瓶的复合材料层的周向及轴向应力远大于未经自紧的气瓶的复合材料层的周向及轴向应力，说明自紧工艺改善了气瓶结构的应力分配。

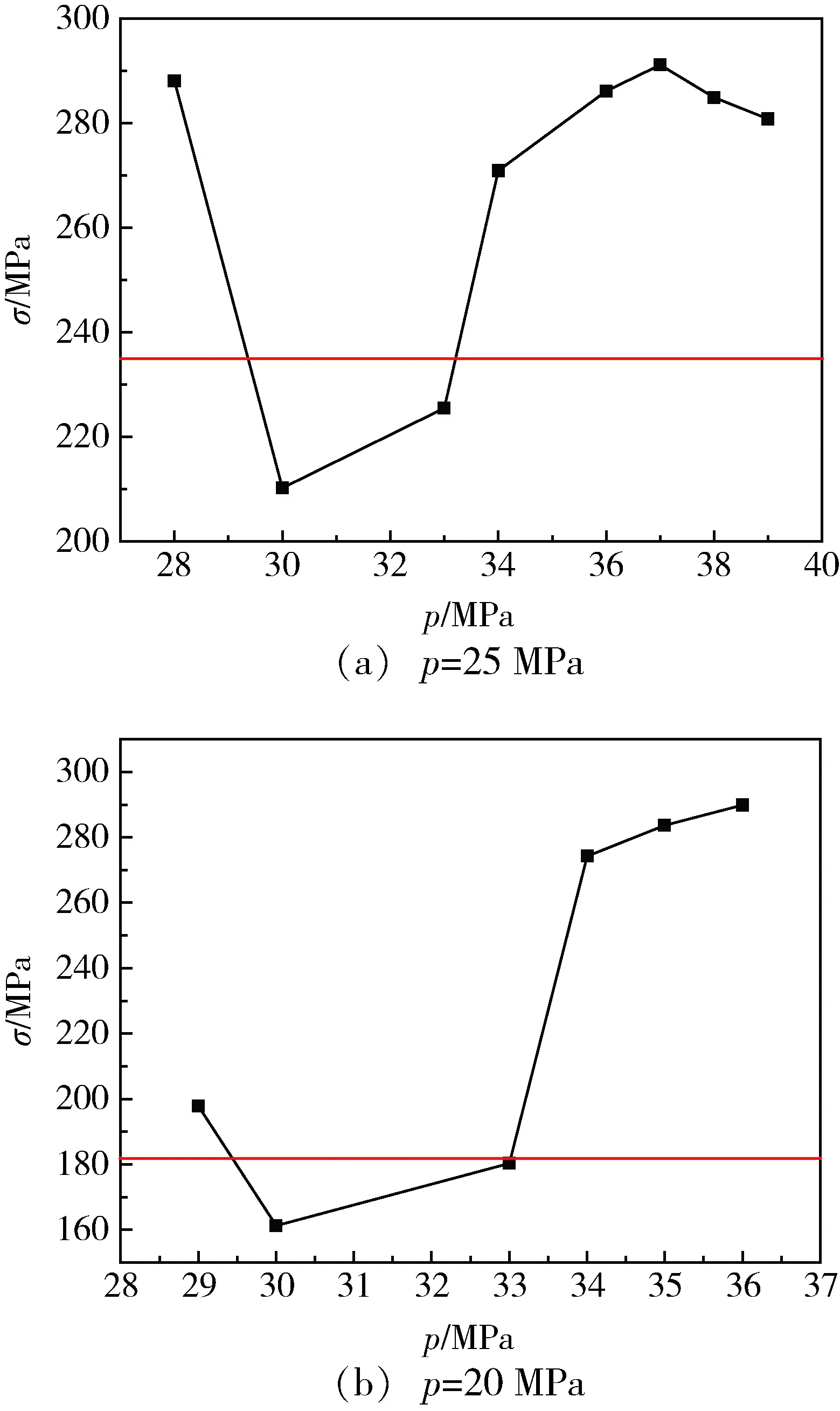
图8 不同自紧力下，内衬应力的变化Fig.8 Stress of liner under different force of autofrettage

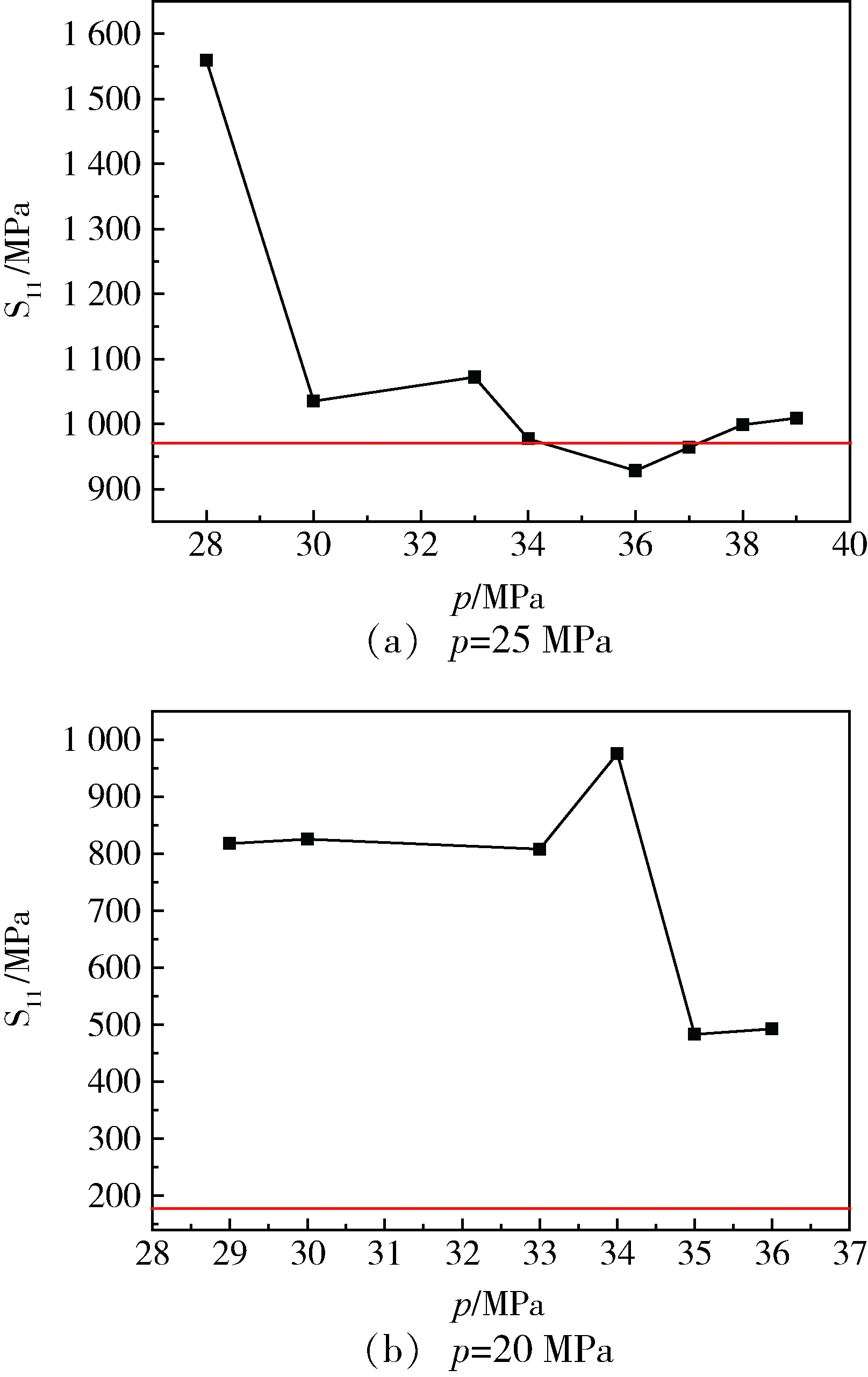
图9 不同自紧力下，复合材料层周向应力的变化Fig.9 Circumferential stress of composite layer under different force of autofrettage

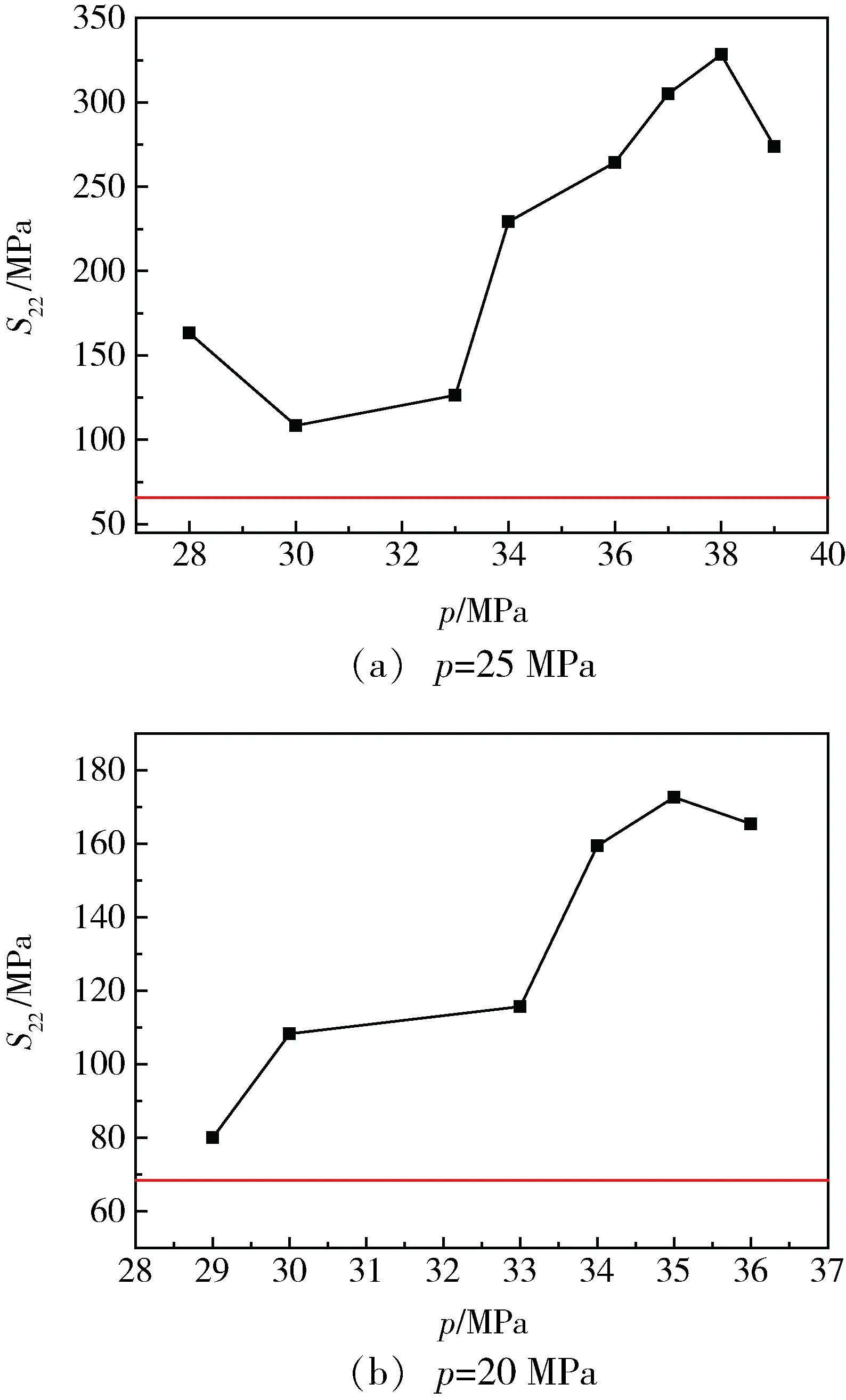
图10 不同自紧力下，复合材料层轴向应力的变化Fig.10 Axial stress of composite layer under different force of autofrettage

根据DOT-CFFC 2007[14]，自紧力下内衬的筒身段必须处于屈服状态，自紧力卸载后内衬层Mises最大应力应大于内衬材料屈服强度的60%，但不得超过其屈服强度的95%。图11是不同自紧力作用下，气瓶卸载后内衬的应力。可知当自紧力为30～33 MPa时，卸载后的气瓶内衬压应力大于屈服强度60%，即177.6 MPa，小于屈服强度95%，即262.2 MPa，满足规定要求。

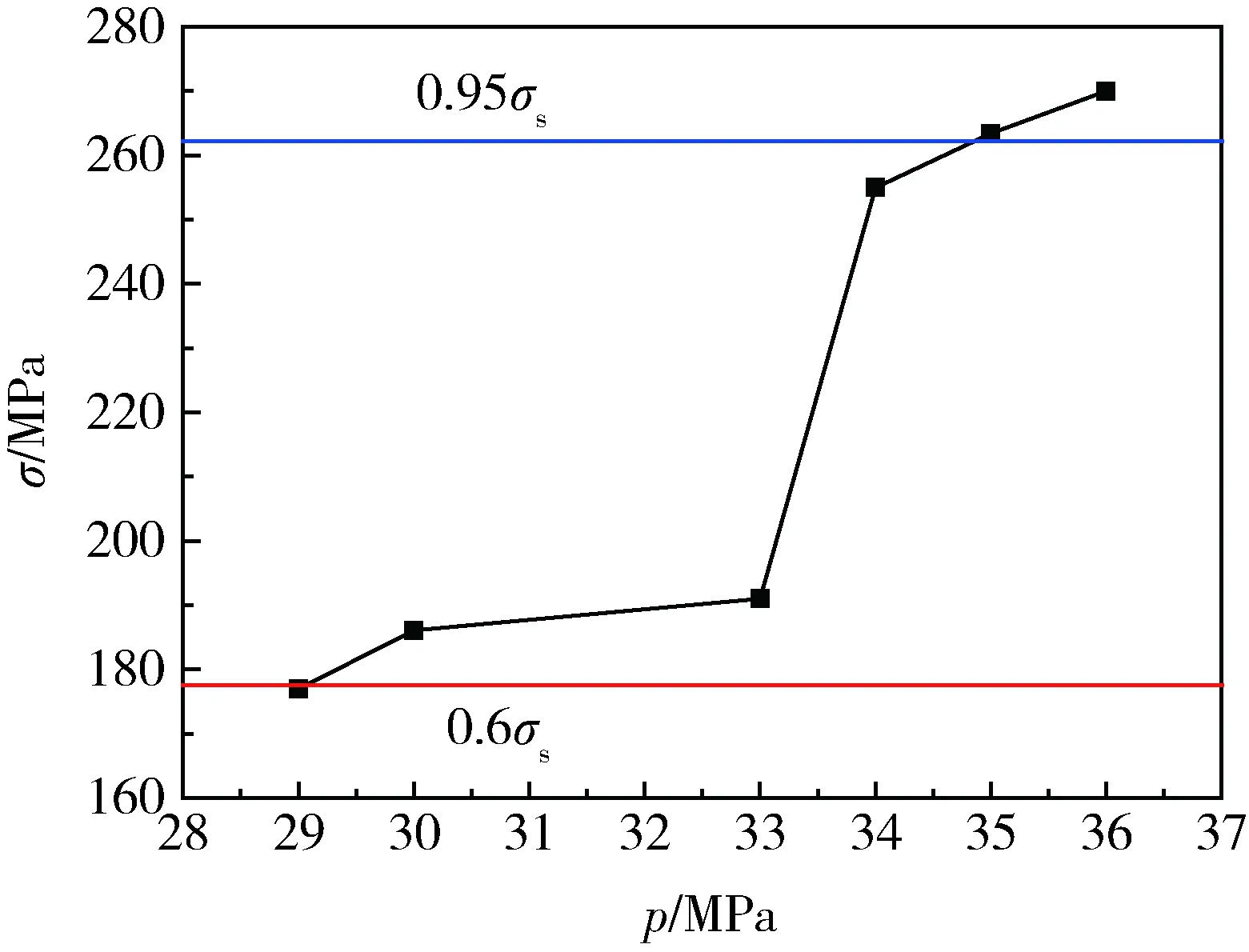
图11 不同自紧力作用，卸载后内衬的应力Fig.11 Stress of liner under load-off after different force of autofrettage

等效塑性应变图描述的是整个过程中结构塑性应变的累积结果[2]。图12是沿路径从极孔顶端到气瓶底部的等效塑性应变的分布情况，可知，30 MPa的自紧力作用时，气瓶筒身段不仅处于屈服状态，且等效塑性应变最大，满足规定要求。

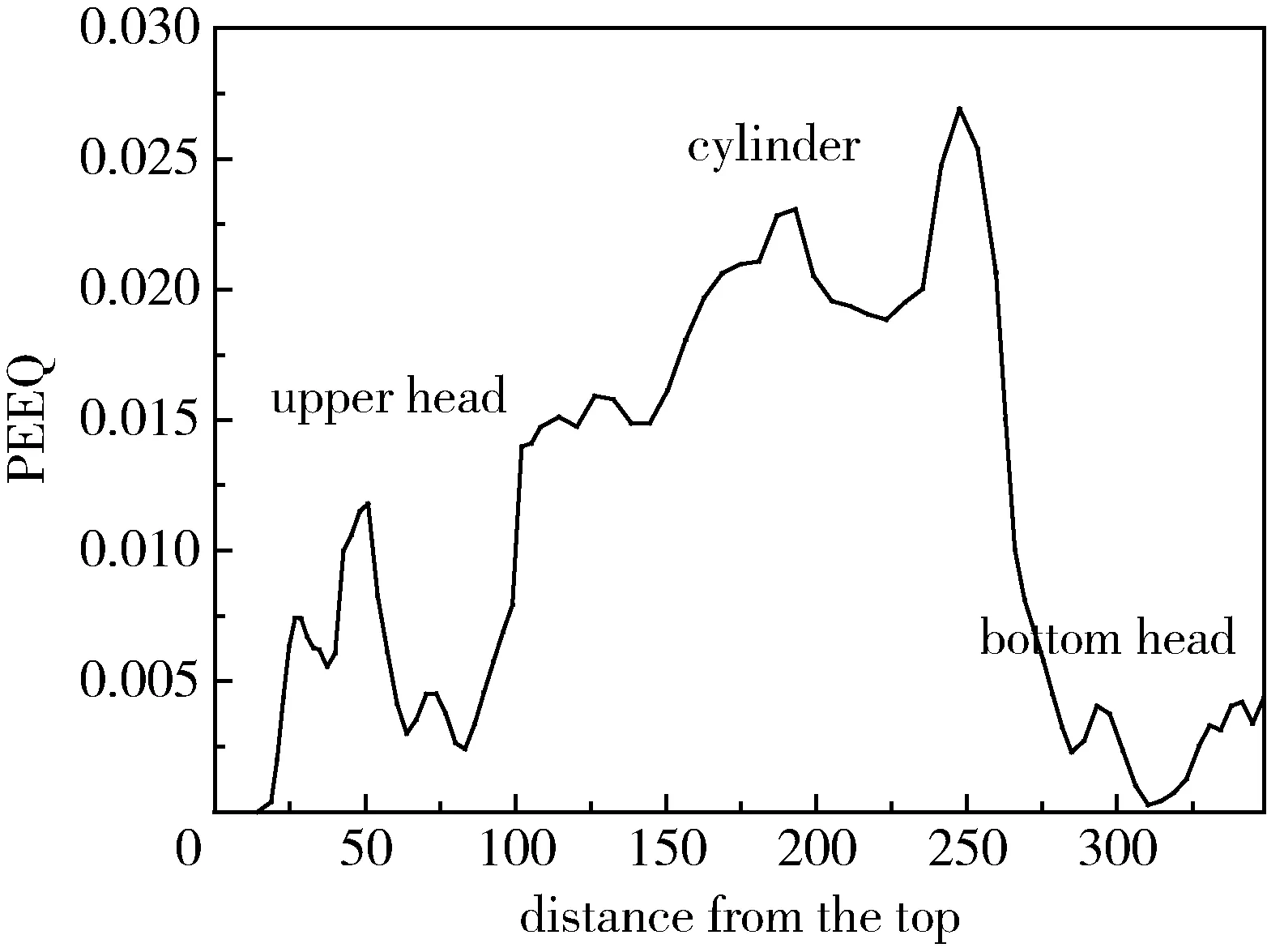
图12 30 MPa自紧力作用时，气瓶的塑性等效应变Fig.12 Plastic equivalent strain of cylinder under 30 MPa force of autofrettage

综上，当自紧力为30～33 MPa，即最大工作压力的1.5～1.65倍时，气瓶内衬应力减小，复合材料层应力大幅提高，气瓶应力分配得到改善承载能力得到提高，是合理的自紧力范围。从减少复合材料的损伤和最大程度降低内衬应力的角度，最优自紧力应为30 MPa，即最大工作压力的1.5倍。

4 结论

本文基于渐进损伤分析的方法，从数值模拟角度分析了气瓶复合材料层渐进损伤发展和累积的过程以及气瓶的应力变化。验证了自紧工艺对提高气瓶承载能力的必要性，确定了合理自紧力的范围，结论如下。

(1)基于复合材料渐进失效分析，全缠绕气瓶复合材料层损伤发生的顺序或可能性：基体拉伸>拉伸分层>纤维拉伸/基体压缩，且损伤大都从螺旋缠绕层开始。除基体拉伸失效由封头向筒体发展，由复合材料外层向内层发展，其余损伤大都从筒体中部向两端发展，由内层向外层发展。对于算例模型，当内压达到34 MPa时，筒体开始出现多种模式的损伤，因此从减少复合材料损伤的角度，自紧力应小于34 MPa。

(2)基于气瓶的应力分析，当算例模型内压为34 MPa时内衬应力开始大幅增加，在46 MPa时应力达到拉伸强度。当内压达到40 MPa时，复合材料层周向应力大幅增加，到44 MPa时应力激增。内压分别在34和40 MPa时，复合材料层轴向应力大幅增大。因此从应力变化的稳定性角度考虑，自紧力应小于34 MPa。

(3)基于气瓶的自紧工艺的研究，当自紧力为最大工作压力的1.5～1.65倍时，气瓶内衬应力减小，复合材料层应力大幅提高，气瓶的应力分配得到改善，是合理的自紧力范围。从减少复合材料的损伤和最大程度降低内衬应力的角度，最优自紧力应最大工作压力的1.5倍。