基于网络结构化指标的网络节点重要性评估算法

田由

（广州杰赛科技股份有限公司，广东 广州 510310）

1 引言

随着移动通信技术的发展，移动社交网络的数据量呈现爆炸式增长。基于通信移动数据的社交关系分析、社交网络的链接关系分析的研究层出不穷。复杂网络的社交关系以及链接关系预测都与节点的重要性具有密切关系。节点的重要性评估算法已经发展得相当成熟。基于节点度或者邻居节点度的数量来评估网络的节点重要性[1-3]，这类研究在蛋白质网络、食物链网络以及交通网络上具有一定的实证依据，节点的度数越高，其节点表现越关键；基于介数的节点重要性评估最开始是用来个体衡量社会地位的一个指标[4]，其核心思想是经过一个节点的最短路径越多，则该节点的影响力越大；Kitsak认为度、介数的方法并没有真实反应网络中节点的位置，因此提出了一种利用K-shell的方法来衡量节点的重要性，但是K-shell在一些网络如Barabasi-Albert网络无法区分节点的重要性。

本文考虑到移动社交网络的复杂性，提出一种基于网络结构化指标评估移动用户重要性的算法，该算法的创新性在于：通过划分社团的方式对庞大、复杂的网络进行分组，通过分组的方式避免了传统全局性计算算法所面临的计算时间复杂度的问题；然后对每一组的网络采用聚集系数和网络重要度来评价移动社交网络节点的重要性，聚集系数能够反映节点与节点之间的紧密程度；网络重要度能够反映节点对整个社团的重要性贡献程度，反映了节点的信息在整个网络中的传播效率。

2 相关研究

2.1 移动社交网络的构建

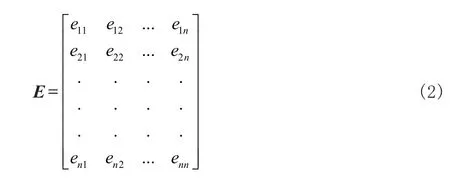
移动用户社交网络可以描述为：存在某种社会关系或者具有相似兴趣的用户通过移动社交工具进行联系所形成的虚拟的社交网络[5]。假设移动用户的社交网络可用无向图G=(V, E)表示，其中，图G包含n个节点和m条边。V={v1,v2, …, vn}E×E表示移动用户社交网络中移动用户的集合。E={e1, e2, …, en}表示移动用户社交网络中用户边的集合，如果存在边，则表示用户之间存在联系。

2.2 社团划分

众所周知，社交网络的每一个节点代表一个移动用户，用户之间通过互相联系构成了整个移动社交网络的结构。网络中有些移动用户之间联系较为紧密，有些移动用户之间的联系则较为稀疏。社团划分把网络内部联系较为紧密的节点划分成为多个社团，划分的最终结果就是社团内部的节点之间有较为紧密的连接，社团之间的节点连接则较为稀疏。

目前，划分社团的方法有很多，根据重叠性可分为重叠性社团划分和非重叠性社团划分。考虑到移动通信的网络特点，本文仅研究重叠性社团划分的算法，包括Palla等人[6]采用派系过滤算法（Clique Percolation Method，CPM）来划分社团，使得社团划分更加贴近现实；针对CPM算法效率底下的问题，Lancichinetti等人[7]从网络局部结构提出了基于局部扩展思想的重叠社团挖掘算法（Local Fitness Measure，LFM），提升了社团划分的速度；Ahn[8]提出一种基于边相似度的指标来衡量节点之间的紧密度，采用层次聚类算法来实现重叠社团的划分。本文选取CPM算法来划分移动社交网络的社团，针对该算法的缺陷，采用词频-逆文件频率（Term Frequency-Inverse Document Frequency，TF-IDF）算法对移动社交数据进行预处理，剔除大量的非紧密联系的节点，降低算法的复杂度。

2.3 节点重要性评估算法介绍

（1）度的算法

节点的度定义为节点的邻居数量。通过连接节点数量来衡量一个节点的重要性，在某些网络中是简单而有效的。但是，该方法仅仅考虑了节点本身的连接数量，没有考虑节点在网络中信息传播的作用以及位置信息，也没有描述邻居之间的连接状态。因此，该方法并不能很好地描述社交网络等复杂网络的节点重要性。

（2）介数

介数是衡量一个个体的社会地位的指标，定义为网络所有最短路径中经过该节点的数量。如果两个节点之间的最短路径经过该节点的数量越多，那么意味着该节点拥有越多的社会资源。介数是一个全局向量，因此其计算时间复杂度较高，不适合大规模的网络。

（3）聚集系数

聚集系数（也称群聚系数、集群系数）可以反映一个节点的邻居节点之间的紧密程度，是衡量网络传递性的一种度量指标。

Ei表示节点i与所有相邻节点之间相互连接边的数量；ki表示节点i的所有相邻节点的数量。

（4）K-shell算法

K-shell算法采用递归的方式剥离网络中度数小于或等于k的节点，利用该方法获得一种节点重要性排序的指标。具体的划分过程为：

步骤1：从节点的度数角度出发，首先删除度数为1的节点，删除之后网络会出现新的度数为1的节点，重复删除步骤，直至网络中没有度数为1的节点，此时所有被删除的节点构成第一层，即1-shell，节点的Ks值等于1。

步骤2：继续对度数为2的节点重复上述删除操作，被删除的节点构成第二层，即2-shell，得到Ks值等于2的第二层。

步骤3：依此类推，直到网络中所有的节点都被赋予Ks值。

（5）网络重要度贡献

节点对的效率eij是指节点vi到vj的距离dij的倒数。当节点vi与vj是相邻节点时，eij的值最大，即eij=1；当节点vi与vj是互不相邻节点时，eij∈(0, 1)。节点对的效率表征了节点之间的相互作用，如果一个网络中存在n个节点，那么网络效率可以表示为：

网络效率不能很好地反映某个节点与其他节点的相互作用的大小，因此，本文参考相关研究[9]，采用效率矩阵的节点重要度贡献方法，来衡量一个节点在全网中的重要性。

那么，第i个节点在整个网络的重要性为hi。

3 基于网络结构化指标评估移动用户的重要性

3.1 数据预处理

如果用户之间采用移动社交工具产生联系，那么两个用户之间存在一条边。这条边的大小可由移动用户之间的交互次数来衡量。一旦移动用户产生一次交互，那么两个移动用户之间添加一条边。但是，根据这种算法得出的移动用户关系难免有点不合常理。众所周知，一些公共电话、中介电话等一些非重要的群体可能会被纳入该社交网络中，导致算法的计算复杂度变高。因此，本文采用TF-IDF值来衡量两个移动用户之间的社交关系强弱。

tfuv代表用户u和用户v之间的交互次数，idfuv代表用户u和用户v之间的交互次数与用户v和所有用户之间的交互次数的占比。采用TF-IDF值来衡量用户之间的关系，能够在一定程度上剔除公共号码等非重要群体，降低算法的复杂度。

3.2 采用CPM算法实现社团划分

在衡量网络节点之前，需要对网络进行社团划分。如此，不仅可以降低衡量节点重要性的计算复杂度，还能从社区内部关系紧密、具有相似结构的节点中挖掘具有重要位置作用的“核心点”，提高算法的精度。

基于CPM算法的步骤是：

（1）步骤一：采用迭代递归的方法来挖掘满足交互次数的大小不同的派系。在第一步数据预处理的基础上，提取移动社交网络中交互次数大于特定值的节点集合；然后从该集合中随机一个节点出发，找到包含该节点的大小为g-1的派系并删除该节点以及其连接的边；接着另选一个节点重复上述的步骤直至该集合没有节点为止。

（2）步骤二：重复上述的步骤寻找g-2派系，…，k派系，当g=k时，算法结束。

（3）步骤三：对上述的派系建立派系重叠矩阵C，根据用户输入的k值以及派系重叠矩阵构建派系的连接矩阵，发现k-派系社团，实现重叠矩阵的挖掘。

3.3 基于网络结构化指标评估社团中的重要节点

社交网络具有传播信息实效性强、重要节点影响力深远的特点[10]，为了充分突出社交网络的结构化、层次化，本文对网络节点重要性评估的指标选取聚集系数以及网络重要度两个指标。结合节点的聚集系数和网络重要度考虑，得出一种新的参数来评估某个节点在社团中的重要性：

其中，g(Ci)表示聚类系数的标准化计算，Ci为节点i的聚类系数；g(hi)表述网络重要度的标准化计算，hi为节点i的重要度。

3.4 实验结果

本文选取某地市的500名移动用户进行实验，实验的目的是通过多种方法对比，来证明本文提出方法的准确率是满足工程应用的。经过TF-IDF进行数据预处理后，将剩下的397名移动用户放进模型中，经过一系列的操作，包括社团划分、重要节点提取后，得出的实验结果如表1所示：

表1 各节点指标值的排序（选取前10个重要节点）

从表1可知，针对500名移动用户的信息发布、传播以及节点的交互次数进行评分后，得到的Top10的排名是：215-623-599-753-452-750-532-612-933，影响力最高的是代号为215的移动用户，其次为代号为623的移动用户，以此类推。本文把各种算法得出的500名移动用户的影响力进行排名，并把排序分成50个区间，把各个区间集合与真实排序对应区间集合求交集，形成区间的准确率。在此基础上，对每一个区间的准确率进行加权平均达到综合准确率。例如：上表Top10排名显示第一个区间的划分情况，本文方法的区间内的代号与真实排序的区间代号求交集为{215, 623,599, 753, 452, 750, 532}，那么第一区间的准确率为7/10=70%。同理，遍历所有的区间并求出各区间的准确率后进行加权平均得到综合准确率。各种方法影响力排名的准确率如图1所示：

图1 各种方法的准确率对比

从图1可知，本文提出的方法的准确率比传统方法的准确率略高。经过社团划分后再进行重要节点提取的方法在理论上应该比介数、聚类系数和K-shell的方法计算复杂度低，但是由于本文样本数量的限制，无法从不同数量级别上进行对比，样本量过少无法凸显本文算法的速度优越性，这个问题将会在样本数量满足条件的基础上进一步进行证明。

4 结束语

本文利用移动通信用户的社交数据构建移动社交网络，采用一种基于网络结构化指标评估移动用户重要性。实验证明，结合节点的聚集系数和网络重要度考虑的方法比传统的方法准确率高。由于样本数量的条件限制，无法进一步对比本文提出的先划分社团再提取重要节点的方法在速度上的优越性，这将会在样本数量满足条件的基础上进一步进行证明。