Arnold变换与伪魔方变换在图像置乱中的研究

李 博

（郑州成功财经学院，河南 巩义 451200）

随着互联网越来越融入我们的日常生活，通过网络获取各类信息资源已成为一种主要的途径，开放的网络平台在给大家提供便利的同时也带来了安全的隐患。为了保障信息的正常传播，数字产品的安全，保护版权所有者的权利，很多专家学者都对数字信息的安全保护进行了深入研究，并取得了很大的进展。宋莉莉等[1]利用Arnold置乱的简单易懂性以及Gray码能灵活应用在位置空间等特点提出了一种基于Arnold与Gray码变换相融合的双置乱算法，使得加密信息在位置空间和灰度空间上都得到很好的隐藏。吴成茂[2]利用二维Arnold变换构造三维结构，将平面图像一一映射为立体空间二值图像，对其像素位置的置乱和恢复间接地改变了平面图像的像素位置和像素值大小，同时结合小波变换及信息论的方法实现了图像置乱。梁婷等[3]对传统的仅适用于正方形区域的Arnold变换的置乱算法进行改进，提出了一种新的多区域置乱算法的图像加密模型，该模型对于非正方形图像采用划分多区域，分别对每个区域进行置乱的方法，有效地提高了图像的安全性。占履军等[4]利用Arnold置乱和采样置乱对水印进行二重加密，与一重置乱加密相比，二重置乱的鲁棒性最好，且能够同时保护两人共有的图像版权。

1 图像置乱方法

图像置乱是充分考虑像素的相关性，结合各种常用的变换方法，形如Logistic变换、Arnold变换、Hilbert变换、Gray码变换等，从空域上直接改变图像的信息，经过置换后的像素相关性被破坏，使得加密的图像信息能够在网络传输过程中得到安全传输。Arnold变换是常用的置换方法，简单易懂，但是因为周期性强的特点，安全性得不到保障。本文引入伪魔方变换，并结合使用Arnold变换，很好地提高了数字图像的抗攻击性。伪魔方变换可以很好地降低图像的失真，并且对可穷举性攻击有很好的抵御能力。

2 Arnold变换与伪魔方变换

2.1 Arnold变换

Arnold变换又称为猫脸变换，通过置乱的方法可以使一幅正常的图像变得无意义，过程定义如下。

对于任意的N*N矩阵，设i，j为矩阵元素，经过Arnold变换后新的矩阵元素为i'，j'，且满足下式：

其中i,j:0,1,.........N-1，N为图像的长或宽。经过多次变换可以消除图像的原始相关信息，但是Arnold变换具有一定的周期性，经过周期性的变换后，矩阵回到原始状态, 复原初始图像，具体如图1所示。

图1 Arnold变换及周期特性

图1（a）是一幅512×512大小的lena原始图像，经过10次置乱后的图像如图1（b）所示，经过一定周期后重新恢复出原始图像，图1（c）为周期性置乱后的图像。通过分析可知，Arnold变换的编程实现简单，但是周期性强，也使得攻击者能够通过穷举攻击，截获相关信息。为了提高网络传输信息的安全性，Arnold变换还需要进一步研究。

2.2 伪魔方变换

通过利用骑士移动技术[5-7]打破个别数字低阶和高阶模式获得魔方矩阵，N阶的魔方矩阵可以通过以下公式获取。

其中，x,y∈[-N/2,N/2]，假设N是奇数且A≠B，A,B∈[2,N-2]，因此魔方矩阵的元素取值范围为[0,N2-1]。伪魔方矩阵是一种没有严格限制形式的矩阵，假设A≠B，不管N是奇数还是偶数，A,B∈[1,N]。通过利用公式（3），改变x,y∈[N/2,N/2-1]，A和B的值，得到伪魔方矩阵。N阶伪魔方矩阵的个数通过下面公式获取：

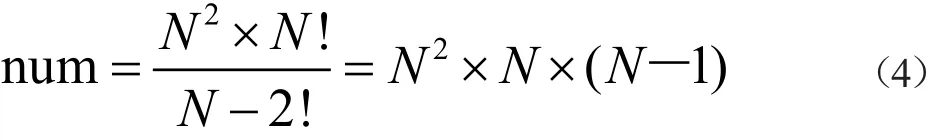
通过公式（4）计算可知，当N为7阶魔方矩阵时，可以获得2 058个伪魔方矩阵。图2是魔方矩阵和伪魔方矩阵的一个示例。

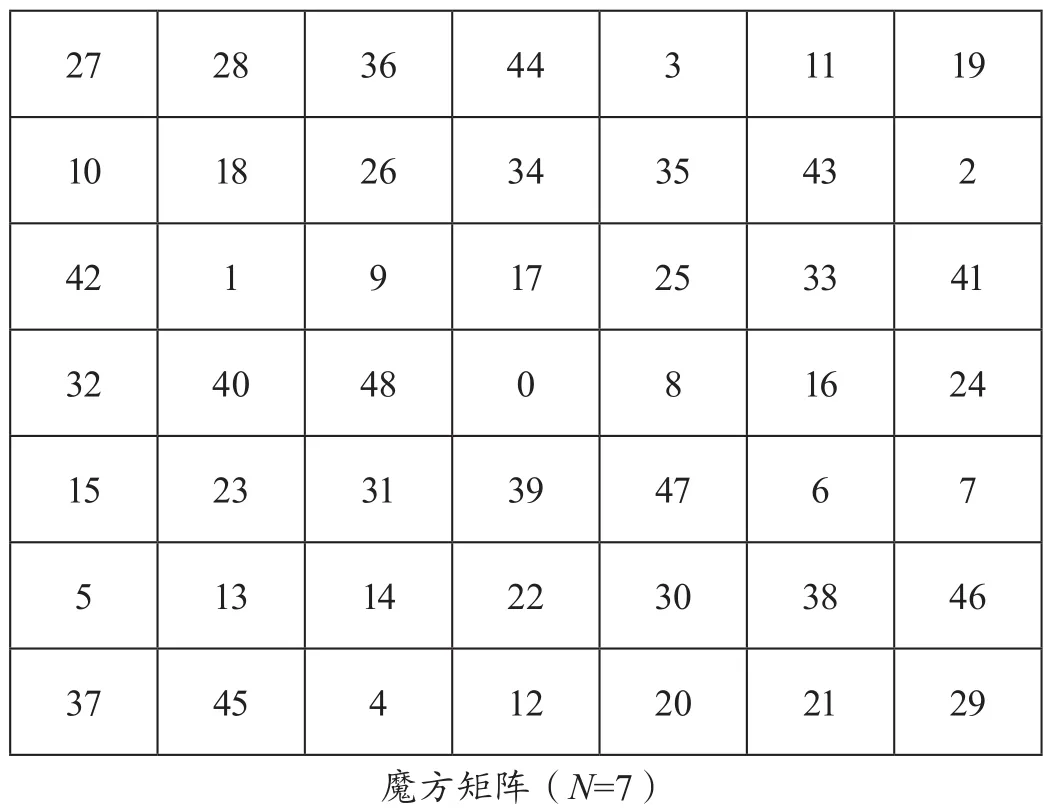
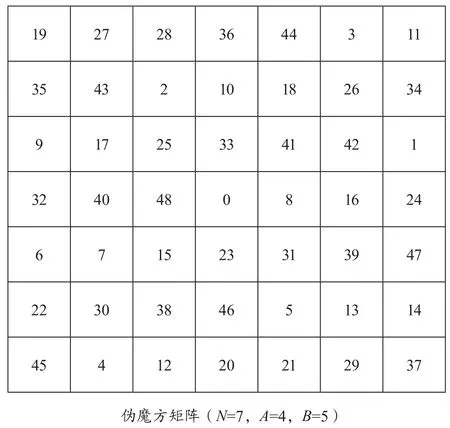
图2 魔方矩阵和伪魔方矩阵

3 Arnold与伪魔方变换的双置乱算法

通过上述的简单介绍，了解到Arnold变换可以改变数字图像的像素值分布，从而达到对信息的加密，但是，由于Arnold变换具有很强的周期性这一局限性，使得加密信息对穷举性攻击的抵抗力较弱，所以在实际应用中的推广使用具有很大的局限性。伪魔方变换产生的伪魔方矩阵关键在于N，A，B的取值，接收方和发送方每次进行消息传播的时候都不使用同样的参数取值，这在很大程度上提高了信息的安全性。本文着眼于利用Arnold变换的简单性和伪魔方变换的机密性，提出Arnold和伪魔方变换的双置乱算法。基本原理是，首先将原始图像进行Arnold变换，然后根据图像的实际大小信息，将变换后的图像进行分块，比如分成7×7大小的子块，将每一个子块进行伪魔方变换。

假设A为原始图像，大小为N×N，B为置乱后的图像，具体的置乱加密过程如下。

步骤1：对图像A进行Arnold变换；步骤2：对步骤1中的图像进行分块，子块大小为7×7；步骤3：按照从上到下，从左到右的顺序依次处理像素对（x，y），并代入公式（3）中进行处理得到相应的函数值，通过查找对应的伪魔方矩阵得到下标值，将伪魔方矩阵中0的下标值（4，4）与之对应相减，得到差值对（xd，yd），利用公式（1）和公式（2）修改像素对的取值，最终得到置乱加密后的图像B。

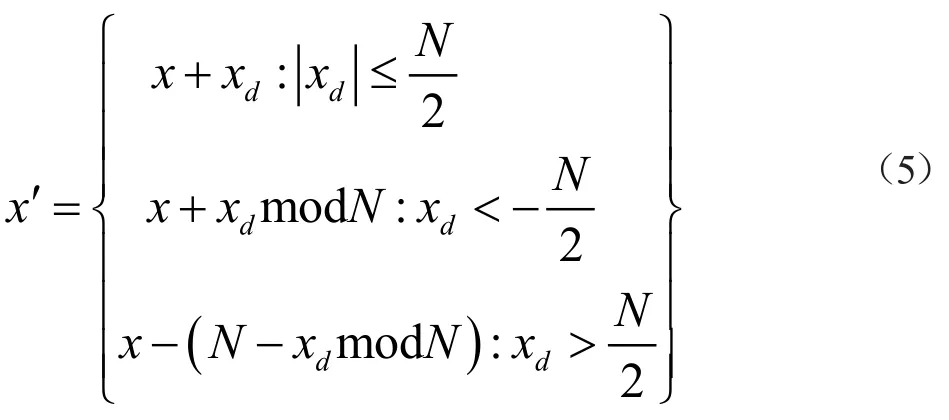
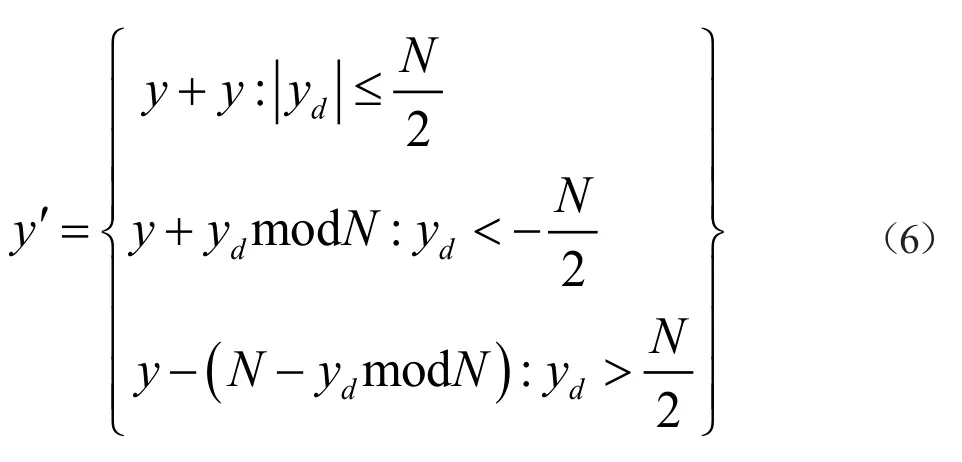
接收者通过公共信道收到置乱加密后的信息，需要恢复原始信息，具体的实现过程如下：

步骤1：对图像B进行分块，子块大小为7×7。

步骤2：利用公式（3）和公式（4）的逆运算对子块像素进行计算，得到第二次置乱前的像素信息。

步骤3：对步骤2中的像素信息进行Arnold逆变换，或者利用周期性特点进行原始图像A的恢复。

4 结果分析

本文使用一幅512×512的lena图像进行数据分析，截取其中子块的信息进行典型案例分析。原始图像的左上角7×7子块像素信息如图3所示。

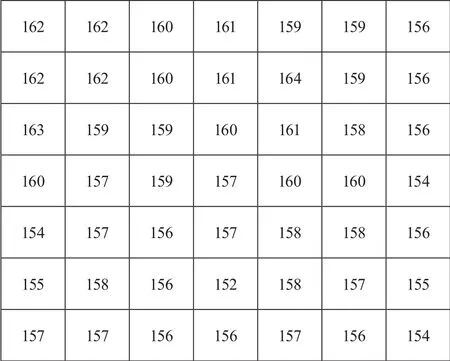
图3 原始图像7×7子块像素信息

第一次Arnold变换经过10次迭代置乱后的子块像素信息如图4所示。

第二次伪魔方变换（A=4，B=5）后的子块像素信息如图5所示。

经过Arnold变换和伪魔方变换，可以提高可穷举行攻击，实现了对图像深层加密的目的，对数字图像在公共信道上安全传输奠定了技术基础。

图4 第一次Arnold置乱后像素信息

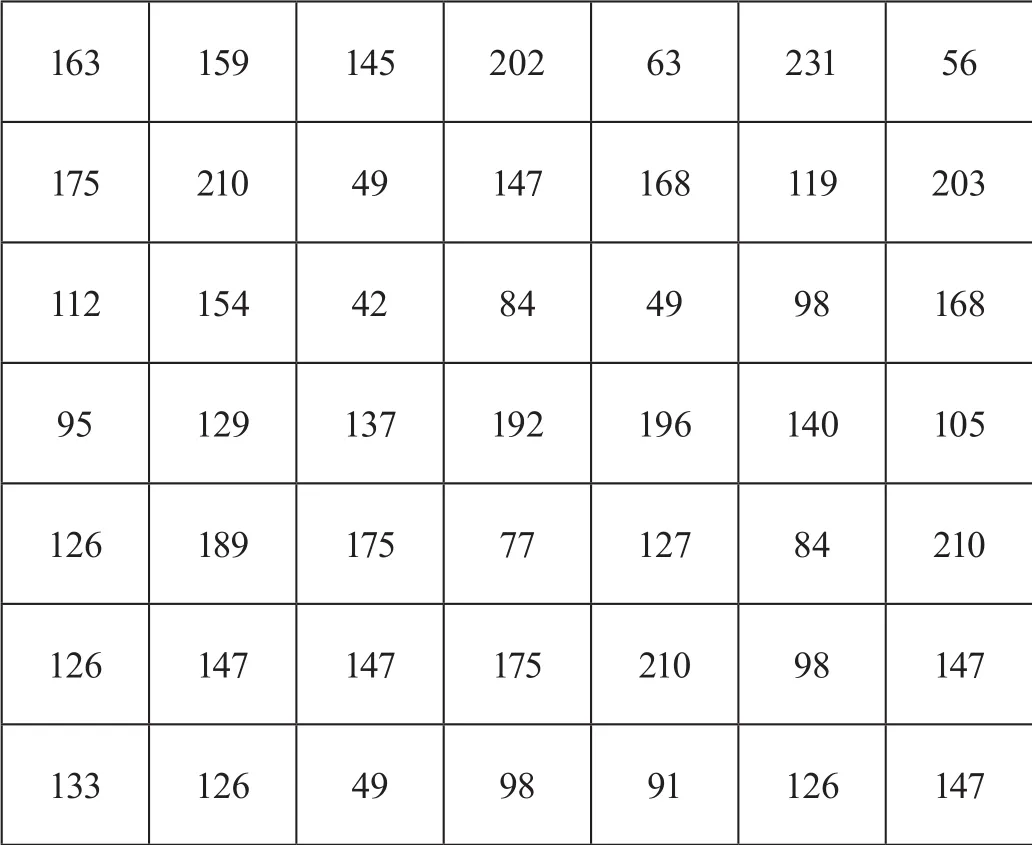
图5 第二次伪魔方变换后像素信息

5 结语

在图像置乱方法的研究中，Arnold因为简单易实现性得到了广泛应用，但是周期性强局限了进一步的推广，通过穷举攻击可以截获其相关信息；伪魔方变换在不同的信息传递过程中可以使用不同的参数，可以有效抵抗穷举攻击。因此，本文在利用Arnold变换基础上结合伪魔方变换的多样性提高了公共信道传输的安全性，也为实际应用奠定一定的技术基础。