基于小波变换的相控阵全聚焦图像去噪

， ，，，振光

(广东省超声电子重点工程技术研究开发中心， 汕头 515041)

相控阵技术作为超声波检测领域的一种快速、高效的成像检测技术，已经有40多年的发展历史。高速处理器的不断发展以及先进成像算法的研究推动了相控阵超声成像技术的发展。近几年，国外相控阵研究人员提出了一种基于相控阵系统全矩阵数据采集的全聚焦超声成像技术。全矩阵数据采集方式的工作原理是：利用全矩阵数据采集得到的采样数据，基于相应的自定义聚焦成像模型，形成的检测图像叫做全聚焦图像[1]。依次激发阵列换能器的单个阵元，同时所有阵元进行接收，对于阵元数目为n的阵列探头，最终将采集到n×n条A型波原始数据。很明显，全矩阵数据的这种采集机制是基于声束半扩散角原理进行的，即单个阵元发射声场的半扩散角范围内所覆盖的所有缺陷的反射回波信息均能够被接收阵元接收到，全聚焦法则根据声波传播时间进行图像重构的过程中，缺陷回波信息在同相叠加到缺陷真实位置的同时，也会在半扩散角范围内以弧面的方式发生扩散，因此在形成全聚焦检测图像的计算过程中，不可避免地会将不同缺陷的反射回波数据叠加到错误的位置，从而引入背景噪声，影响实际缺陷的识别以及定性、定量测量[2]。为了获得理想的图像检测效果，全聚焦图像的去噪声算法研究是一项很重要的工作。

小波变换是在短时傅里叶变换的基础上发展起来的一种变换方法，具有多分辨率分析的特点，在时域、频域都具有较强的表征信号局部特征的能力。其通过伸缩、平移等运算功能对信号进行多尺度细化分析，能有效地从信号中提取信息。噪声通常具有高频特性和空间不相关性，噪声图像经过小波变换后可以得到低频部分和高频部分，低频部分体现了图像的轮廓，高频部分表示图像的细节以及混入的噪声。因此，对图像进行去噪声处理需要在小波域内对高频部分系数进行阈值处理，将处理后形成的新的高频部分与低频部分结合，重构降噪图像，从而实现图像的去噪声处理。

1 全聚焦重构噪声分析

使用一个具有n阵元的一维线性阵列探头进行基于全矩阵数据采集的实时全聚焦成像，将检测区域按照自定义的某一特定分辨率进行网格化处理，假设在网格内即被检工件内部坐标为(x,y)位置处有一个缺陷反射体，使用全矩阵数据对该缺陷对应的像素强度Ixy进行全聚焦重构，计算公式为

(1)

式中：Sij为全矩阵数据集合，第i阵元发射，第j阵元接收；Dixy为第i阵元到坐标(x,y)的声波传播距离；Djxy为坐标(x,y)到 第j阵元的声波传播距离。

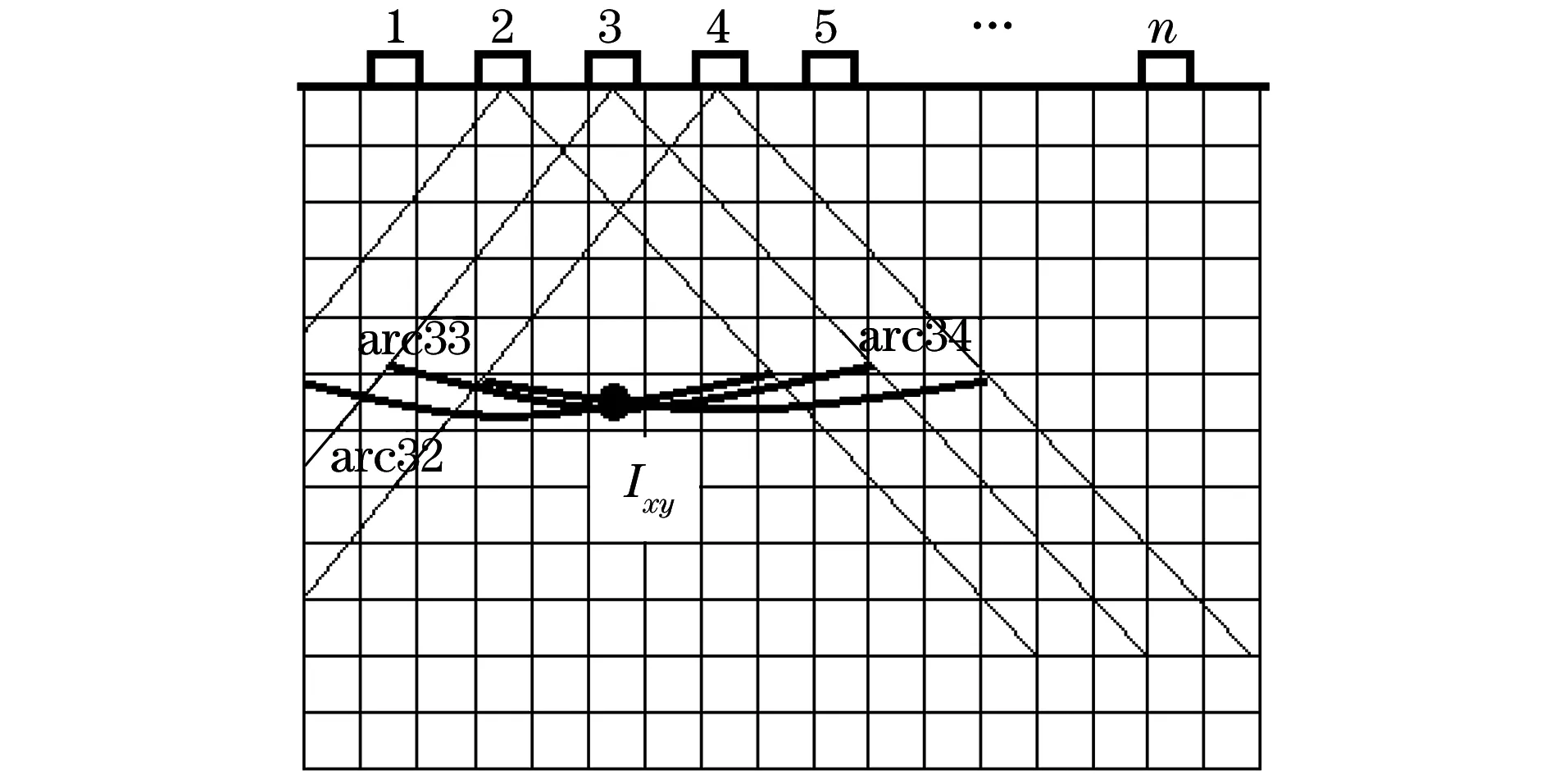
图1 全聚焦法则计算模型

图1所示为全聚焦法则计算模型。S33(D3xy+D3xy)为阵元3发射，阵元3接收，采集到(x,y)位置处缺陷的反射回波；S32(D3xy+D2xy)为阵元3发射，阵元2接收，采集到(x,y)位置处缺陷的反射回波；S34(D3xy+D4xy)为阵元3发射，阵元4接收，采集到(x,y)位置处缺陷的反射回波。按照全聚焦法则进行计算，3个缺陷回波的数值在网格内的(x,y)位置处实现了缺陷回波的同相叠加；然而，事实上每个缺陷回波的数值在全聚焦计算过程中不仅被同相叠加到了网格内的(x,y)位置处，而且为了达到全聚焦的目的，算法将每一次收发采集到的(x,y)位置处的缺陷回波分别累加到了以阵元j中心为原点，Dixy+Djxy为半径，扇形角度为两倍半扩散角的圆弧面arc33、arc32、arc34上，从而给全聚焦的计算结果带来了一定程度的背景噪声。当工件内部缺陷数量比较多、个体比较集中的情况下，这种背景噪声的强度会比较大，从而影响对真实缺陷的识别。

2 算法及其实现

基于两级小波变换的全聚焦信号去噪算法的步骤如下：全聚焦信号通过小波滤波器组分别进行高通、低通滤波，分解后的高频子带系数做无偏似然估计的自适应阈值去噪声处理，再对低频子带系数和处理完的高频子带系数进行小波逆变换，重构去噪声处理后的全聚焦信号。

2.1 小波函数的选择

小波函数具有多样性，不同的小波函数具有不同的特性，不同性质的小波对去噪声效果有着直接的影响。Daubechies小波具有紧支撑性和正交性，紧支撑特性能够消除边界效应，正交性能够使得重构信号获得较好的平滑效果。根据消失矩N的不同，Daubechies小波可以简单表示为dbN。消失矩越大，会使更多的小波系数为零，小波系数能量更为集中，从而有利于数据消除噪声。但是在一般情况下，消失矩越大，支撑长度就越长，会产生边界效应。

综合考虑支撑长度和消失矩，选取db4小波变换(见图2，图中横纵坐标数据无量纲)，db4尺度函数对应于小波分解低通滤波器，db4小波函数对应于小波分解高通滤波器。

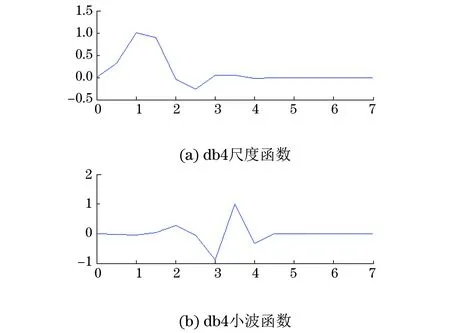
图2 db4小波变换

2.2 去噪声算法

实际应用中的噪声信号标准差σ一般是未知的，需要通过有效的方法进行估算。因为噪声主要集中分布在小波分解后的高频子带系数上，故可以利用小波分解得出的各级高频子带系数，根据经验值分别估计各级高频子带系数的噪声标准差σ。

σ=median(|X|)/0.674 5

(2)

式中：X为小波分解得出的某个高频子带系数。

将每一级高频子带系数计算平方之后,按照从小到大的顺序进行排列，得到向量SX。

SX=Sort(X2)

(3)

根据向量SX计算风险向量并找出最小风险值R，其中l=[1,2,3,…,N]，I为R在风险向量中的索引值。

[R,I]=

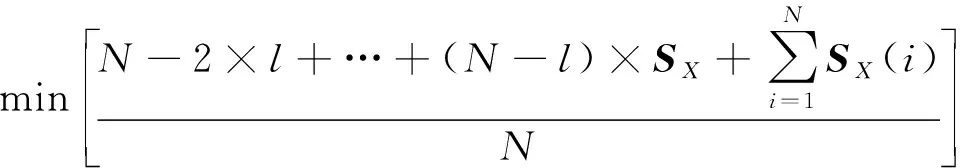
(4)

根据最小风险值R对应的高频子带系数求出阈值T。

(5)

根据阈值T，计算阈值去噪声处理后的高频子带系数Y。

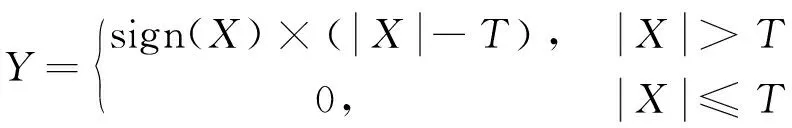
(6)

3 全聚焦图像去噪声试验

采用汕头超声仪器公司的CTS-PA22T超声相控阵全聚焦成像设备和相控阵探头，在几种不同类型缺陷试块上分别进行了16通道的相控阵全聚焦成像检测试验，并存储了相应的缺陷检测图像。选用的相控阵探头型号为4L16-1.0×10。横波楔块参数为：楔块角度36°，中心阵元高度12 mm，楔块中声速2 700 m·s-1。

图3 未融合缺陷全聚焦噪声图像

对一块含根部未融合缺陷的钢板对接焊缝试块进行全聚焦检测(检测结果见图3)。该被检钢板对接焊缝工件的厚度为19 mm，焊缝底部有一个长度为6 mm的人工线切割未融合缺陷，检测成像区域(宽×高)尺寸为50 mm×9 mm(从楔块零点开始)。由于工件内部缺陷数目少,仅有一个底部未融合缺陷，在基于全矩阵采集时声束半扩散角范围内接收到的全矩阵信号间的相互干扰因素少，因此形成的全聚焦检测图像能够有效识别缺陷特征。但是，由于在全聚焦重构的过程中，每条接收波形自身的回波信息被分布到半扩散角对应的整个圆弧面，从而使得未融合缺陷的成像边界比较模糊，难以对缺陷的真实尺寸进行定量测量。图4为该融合缺陷的全聚焦降噪图像，可见通过去噪声处理后，在保证与缺陷信号同等灵敏度的条件下，背景噪声消除得非常理想，图像的信噪比得到了极大改善，有助于缺陷的定量测量。

图4 未融合缺陷全聚焦降噪图像

对一块含根部垂直裂纹缺陷的钢板对接焊缝试块进行全聚焦检测(检测结果见图5)。该被检钢板对接焊缝工件的厚度为25 mm，工件底部有一个高度为9 mm的人工线切割垂直裂纹，检测成像区域(宽×高)尺寸为50 mm×25 mm(从楔块零点开始)。由图5可见，全聚焦检测图像能够真实反映工件底部垂直裂纹缺陷的实际形状，可以对缺陷进行定性。但由于裂纹缺陷的全聚焦重构是基于串列式的声波传递模型进行的，受限于超声波传播的物理特性等多种因素，全聚焦重构图像中伪像问题比较严重，且楔块内部的固定杂波灵敏度也比较高，很可能会造成实际检测过程中缺陷的误判。图6为垂直裂纹全聚焦降噪图像，可见，通过去噪声处理之后，检测结果中的楔块固定杂波以及伪像等干扰噪声均被有效消除，显著地提高了全聚焦检测图像的视觉效果。

图5 垂直裂纹全聚焦噪声图像

图6 垂直裂纹全聚焦降噪图像

对含有一系列不同深度通孔的B型相控阵试块进行全聚焦检测(检测结果见图7)，检测成像区域(宽×度)尺寸为100 mm×100 mm(从楔块零点开始)。由图7可见，由于背景噪声的影响，图像信噪比低，视觉效果较差，可有效检出的通孔缺陷数只有5个，且楔块杂波残留在检测图像中。图8所示为对全聚焦结果进行基于小波系数无偏似然估计去噪声处理后的结果，可见图像信噪比得到了明显的提升，缺陷的检测识别能力也得到了较大的提升，原本淹没在背景噪声里的通孔均被有效地识别了出来，可检测出的通孔缺陷数目多达11个，同时有效地消除了楔块杂波的影响。

图7 通孔缺陷横波全聚焦噪声图像

图8 通孔缺陷横波全聚焦降噪图像

4 结论

提出了一种小波变换结合无偏似然估计的自适应阈值去噪声方法，对相控阵全聚焦检测图像进行去噪声处理。从试验结果可看出，提出的去噪声算法对于相控阵全聚焦图像的噪声消除非常有效，能够有效地消除由于全聚焦重构算法带来的背景噪声、缺陷伪像以及楔块固定杂波，处理后的图像视觉效果得到了明显改善，图像信噪比大大提高，有助于缺陷的定性、定量测量。