精密复杂零件数控加工在线检测误差补偿研究*

□ 毛文亮 □ 杨小平

1.甘肃机电职业技术学院 甘肃天水 741001

2.甘肃农业大学科学技术处 兰州 730000

精密复杂零件数控加工过程中，引起加工误差的因素较多，表现形式、规律各异，很难精确找出各影响因素与加工误差之间的对应关系［1］。如果从精密复杂零件数控加工的精度检测数据出发，分析精密复杂零件检测曲面的测量数据，那么就可以不考虑每个单一因素对零件加工误差的影响，将所有因素产生的误差归结为加工误差［2］。加工误差中具有重复性、稳定性的误差为系统误差［3］，随机产生的误差为随机误差，随机误差具有不确定性［4］。若能将精密复杂零件数控加工中产生的加工误差分解为系统误差和随机误差，进而准确对系统误差进行补偿加工，则可以有效提高精密复杂零件的加工精度。

1 在线检测误差补偿原理

根据精密复杂零件确定检测部位，在计算机中生成检测程序，通过RS 232串行通信接口传输至数控机床。在检测程序的驱动下，数控机床从刀库中调出事先安装好的测头，并按照检测程序规划路径，对所确定的检测部位进行自动测量。测量结果通过反馈系统传输至数控机床控制系统，然后再通过RS 232串行通信接口传输至计算机。将测量结果与检测部位的理想编程坐标进行对比，就可以得到加工误差。根据误差大小，修改数控加工编程坐标代码，进行补偿加工，就可以实现精密复杂零件“加工、测量、补偿加工”闭环制造［5］，其原理如图1所示。

2 在线检测曲面回归模型

2.1 定义

在计算机辅助设计系统中，理想复杂曲面模型广泛采用参数曲面来表示，设u、v为精密复杂零件检测曲面轮廓沿坐标平面两个轴线方向的矢量参数，A（u，v）为精密复杂零件检测部位的实际加工曲面，B（u，v）为精密复杂零件检测部位的理想曲面，ds（u，v）为精密复杂零件数控加工中产生的系统误差，dr（u，v）为精密复杂零件数控加工中产生的随机误差，则有：

根据式（1），设 C（u，v）=B（u，v）+ds（u，v），则 C（u，v）为精密复杂零件检测部位理想曲面与系统误差迭加形成的新曲面。由于理想曲面B（u，v）具有确定性，系统误差 ds（u，v）具有重复性、稳定性，因此将 C（u，v）定义为回归模型，用C（u，v）来描述加工条件下的零件检测曲面。

▲图1 精密复杂零件数控加工在线检测误差补偿原理

2.2 表达

采用双三次B样条曲面来描述精密复杂零件检测部位的曲面模型。为使精密复杂零件检测部位能够得到分片连续的检测曲面模型，设在检测曲面空间给定（n+1）（m+1）个控制点 Gij（i=0，1，...，n；j=0，1，...，m），逼近生成一个n×m次的贝济埃曲面片，如图2所示。

▲图2 贝济埃曲面片

式中：Ui（u）和 Vj（v）为 B 样条基函数；Rij为控制点；h×l为零件检测部位曲面片的数量。

曲面模型就是控制点与基函数张量积的线性组合，因此，式（2）可表示为：

多个三次B样条曲面片的表达式为［6］：

式中：XK为B样条基函数张量积；RK为相应控制点，RK=（xrk，yrk，zrk）T；F 为控制点的数量，F=（h+3）（l+3）。

XK与RK的线性组合就是曲面模型。

2.3 建模

假设从已加工实际曲面上获得了z个检测点的坐标数据 Pw，w=0，1，...，z，且在 u、v 方向上的节点矢量与检测曲面片的数量，以及每一个测点的u、v参数值都已知，那么式（3）中的张量积XK就能够计算出来。基于以上分析，检测曲面控制点的线性回归模型可以用矩阵P表示：

式中：X为零件检测部位曲面模型与每个测点相关的张量积，R为控制点。

检测曲面控制点的线性回归模型最小二乘估计值可表示为：

由于零件表面上加工误差远小于零件尺寸，因此回归模型测点的u、v参数值可以用检测时的理想曲面参数值u、v代替，精密复杂零件检测曲面的估计回归模型可表示为［7］：

残差可表示为：

3 加工误差分解

对于精密复杂零件检测曲面的加工误差分解，笔者采用空间统计分析方法中的莫兰指数统计法进行。莫兰指数显著为正，表示空间分布中相似的观察值趋向于聚集在一起，空间对象存在空间正相关。莫兰指数显著为负，表示空间分布中不同的观察值趋向于聚集在一起，空间对象存在空间负相关。莫兰指数趋近于0，表示观察值趋于独立随机分布，即空间对象不存在空间自相关［9］。因此，只有当莫兰指数趋近于0时，才可认为各个测点的加工误差在空间上是独立分布的，它们之间不存在显著的相关性。

设εi为样本位置点i到理想曲面的法向偏差，ε为z个测量点处ε的平均值，则莫兰指数I可表示为［8］：

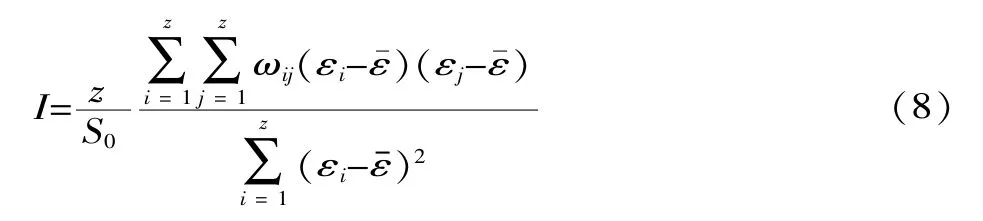
式中：ωij为在位置点i处，位置j对它的空间作用度量权重因数。

检验统计量T可表示为：

式中：μM为莫兰指数均值；σM为莫兰指数方差值。

检验统计量T服从标准正态分布。

随机部分的估计方差σ2μ可用样本方差表示：

为了从取样点的加工误差中分解出随机误差，在拟合回归模型得到残差后，可以通过空间独立分布的零假设检验来确定。如果零假设被接受，则可以认为取样点法向偏差服从空间独立分布，不存在确定性部分，偏差就可以作为随机误差。如果零假设被拒绝，则表明这些误差数据是自相关的，误差值中同时包含随机误差和系统误差，在此情况下，需要进一步寻找，最终使零假设被接受，方可实现误差分解［10］，分别求出系统误差和随机误差。笔者通过对所建立的精密复杂零件检测曲面回归分析模型迭代求取，单侧检验，验证检测曲面回归分析模型接受空间独立分布零假设检验，残差服从空间独立性分布，残差可以作为随机误差。精密复杂零件某一检测曲面分解的系统误差如图3所示，分解的随机误差如图4所示。

▲图3 检测曲面分解的系统误差

4 在线检测误差补偿

根据精密复杂零件数控加工系统误差与补偿点之间的补偿量关系，建立补偿点计算数学模型。设P（u，v）为补偿点补偿值，B（u，v）为理想复杂曲面，s（u，v）为系统误差估计值为 B（u，v）的法矢方向，则有：

根据补偿点公式计算结果，修改数控代码，将理想曲面刀具路径偏移一个系统误差值，生成新的刀具路径，重新进行走刀加工，即可实现精密复杂零件加工误差补偿。

▲图4 检测曲面分解的随机误差

5 试验验证

为验证笔者方法的有效性，采用带发那科数控系统的三轴立式加工中心、雷尼绍触发式测头，对精密复杂零件进行在线检测，并进行误差补偿加工试验，将试验结果与三坐标测量机测量结果进行对比，确认两者基本一致。精密复杂零件数控加工在线检测如图5所示，精密复杂零件数控加工补偿前后数据与三坐标测量机检测数据的对比结果见表1。

▲图5 精密复杂零件数控加工在线检测

表1 精密复杂零件数控加工在线检测误差补偿数据与三坐标测量机检测数据对比mm

6 结论

针对精密复杂零件数控加工中存在的问题，笔者构建了基于B样条曲面的回归分析模型。通过空间独立性分析，将精密复杂零件的数控加工误差分解为系统误差和随机误差。通过补偿点偏差计算，修改数控加工程序，准确对系统误差进行了补偿，实现了精密复杂零件“加工、测量、补偿加工”的闭环制造，有效提高了精密复杂零件的数控加工精度。