一种滤除衰减直流分量的滤波算法仿真

山东玻纤集团股份有限公司 刘文斌

0 引言

当前，微机保护装置中的滤波算法广泛采用傅里叶算法，傅里叶算法具有简单、滤波效果好等优点，但是其缺点是无法滤除衰减的直流分量，而电力系统发生故障时往往含有衰减直流分量，因此研究一种能够滤除衰减直流分量的滤波算法是非常必要的。近年来有大量的科研工作者投入到了此类算法的研究，而此类算法往往是增加采样点数，文献[2]提出的算法理论上不需要增加采样点数，就可以实现对衰减直流分量的滤除，本文的主要工作就是对此种方法进行仿真验证。

1 全波傅里叶算法

以电流为例，设故障输入信号为：

式中：I0为衰减直流分量的初始值，τ为衰减时间常数，In为n次谐波的幅值，φn为n次谐波的初相角，ωn为n次谐波的角频率。上式又可以改写为：

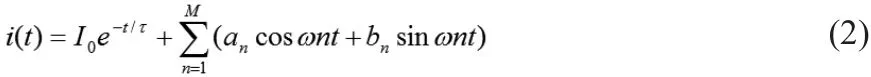
利用傅里叶算法求输入信号n次谐波的正弦分量得：

式中：

同理：

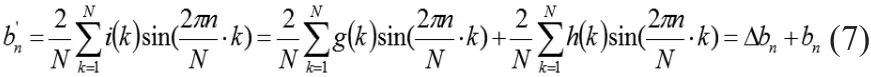
式中：

由上边的分析可知Δan、Δbn分别为输入信号衰减直流分量的正弦、余弦分量，这正是本文要滤除的部分。

2 改进傅里叶算法

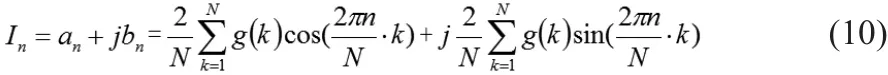
由上式得：

假设基本周期采样点数N为2的整数倍，对采样数列求和：

当N为偶数时：

所以：

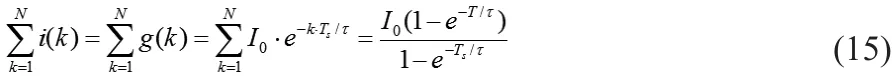
偶数项求和：

对偶数项求和时有：

所以：

设：

由式19和式20得：

可以简化衰减直流分量正余弦分量的表达式为：

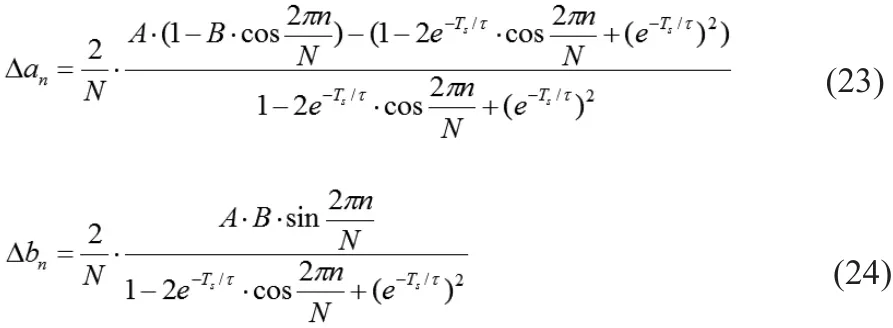
在求得衰减直流分量的正弦分量Δan和余弦分量Δbn后即可求出滤除衰减直流分量后的信号幅值的正弦、余弦分量an、bn。

滤除衰减直流分量后的电流幅值为：

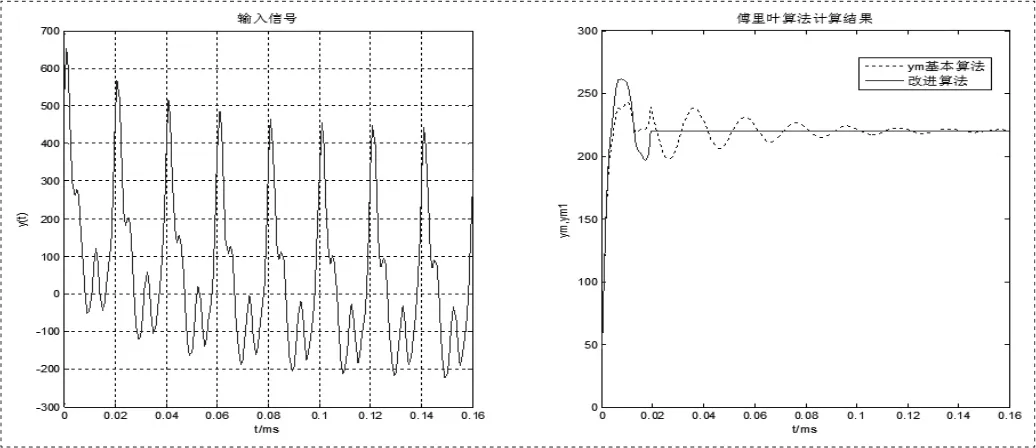
图1 时傅里叶算法仿真结果

3 算法仿真

假设输入信号为：

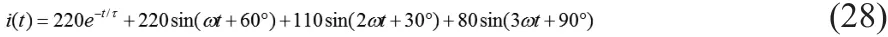
4 结论

从仿真波形可以看出，在第一个周波内，全波傅里叶算法和改进傅里算法都不能滤除衰减直流分量，但一个周波以后，改进傅里叶算法滤除衰减直流分量的效果比较明显，全波傅里叶算法在全程内都无法滤除衰减直流分量。