基于贝叶斯推论的大坝溃口参数预测研究

赵 敏，孙 勇

(贵州大学 喀斯特环境与地质灾害重点实验室，贵阳 550002)

1 概 述

大坝是极其重要的基础设施，是综合防洪工程体系和水力发电工程的重要组成部分，往往规模较大，其价值体现在防洪、发电、灌溉、航运、旅游、水产养殖等多个方面[1]。然而，一旦大坝发生溃决，不仅会造成社会经济损失，更者会导致人员伤亡、生态环境问题等。国内外溃坝事故均有发生，我国1975年的板桥事件造成河南省29个县市、1 100万人受灾，2.6万人死亡，直接经济损失近百亿元[2]。1979年印度曼朱二号水库溃坝事件，造成5 000～10 000人的死亡，经济损失巨大。

大坝溃口形成过程和泄洪过程线(可细分为溃口特征参数、水库蓄水量和下泄流量)的分析对已发洪水的危害评估至关重要[3]。分析大坝破坏以及泄洪水位线有许多模型，其中DAMBRK和HEC-1应用较广，Singh和Snorrason采用这两个模型对20个溃坝案例进行了关键溃口参数的敏感度研究[4]。Petrascheck和Sydler提出了一个数学模型来模拟洪水的外泄过程，研究溃口泄量、洪水位和洪水抵达时间对溃口宽度及溃口形成时间的变化的敏感度。该研究表明，可靠的估计大坝附近及下游区域洪水情况，准确地预测溃口参数是必要的[5]。

对溃口参数的评估有多种方式，Wahl总结为3种：类比法、基于物理原理的模型和预测方程[6]。类比法的前提是大坝间具有相似的几何和水文情况；基于物理原理的模型运用水文学、泥沙运动学模拟溃决过程，往往因为缺乏对溃决机理的了解而过于简化；而预测方程法在今天依然使用最为广泛。预测方程参数一般是通过使用数据库中对有限实例数据回归分析所得最小拟合误差作为唯一指标来得到的，而过度拟合常常导致公式十分复杂并影响预测方程的准确性。

本文运用贝叶斯推论的方法，对ICOLD统计的101个案例数据进行分析，选择最优模型，从而提出可以平衡拟合能力和复杂性的预测方程。

2 溃口参数

溃口参数包括溃口的几何参数、形成时间参数和水文参数。将溃坝理想化为一个不规则四边形，见图1。几何参数即包括溃口深度(溃口高度)Hb(即坝顶至溃口反弯点的距离)、溃口顶部宽度Bt、溃口底部宽度Bb、溃口平均宽度Bave、溃口侧坡因子Z。只要知道其中的任意3个参数就足以描述完整溃口的几何情况。

图1 理想化大坝溃口参数图

溃决时间Tf，Singh和Snorrason定义其为溃裂开始到完成的持续时间[4]。溃口开始时间起始于水流首次流过大坝，此时流出水量较小，随着出流量和侵蚀迅速增加，溃口形成，溃口开始时间终止。溃口形成时间指大坝上游面首次溃决到溃口完全形成的时间。两个参数较难区分。洪峰泄量Qp，取决于水库的水位记录或对侧坡的测量。

基于溃坝的破坏机理，本文中涉及的参数只有4个：大坝宽度Hd、溃口水头Hw(溃口深度Hb)、大坝水库的容积Vd、溃口容积Vw。

3 预测方程参数和模型选择

预测方程可以有加的形式和积的形式。

考虑到测量误差的存在，输出值以预测值和误差项的总和的形式：

(1)

(2)

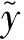
积的形式：

(3)

为了更方便地进行回归分析，对式(3)两边取对数从而转化为加的形式：

lny=β0lnx0+β1lnx1+…+βNxlnxNx

(4)

近10年来，贝叶斯推论被逐渐广泛运用在工程中。为避免过度拟合导致公式过于复杂和影响预测方程的准确性，Yan等人提出了基于贝叶斯推论的模型选择框架[7]。该方法有助于在一系列候选模型中挑选出一个具有最合理的输入输出关系的模型。贝叶斯模型选择框架与现有的预测方程参数只考虑最小拟合误差不同，旨在通过衡量拟合准确度(goodness-of-fit)和鲁棒性(robustness)两者，从而挑选出最合适的模型。模型合理性按下式计算：

j=1,2,…,NM

(5)

(6)

(7)

(8)

(9)

式中：p(Mj|U)为用户对模型Mj的最初合理性的判断；p(D|Mj,U)为给定D时计算模型Mj的一个量；θj为在模型Mj中定义的参数向量，包含着未知拟合参数αj和σε；p(θj|Mj,U)为用户指定的先验概率密度函数；p(D|θj,Mj,U)为模型Mj准确度的似然函数，又写为p(D|θj,Mj) ；Jg(α|D,Mj)为在拟合系数α下的准确度函数；Nj为模型Mj中不确定参数数量。

式(7)p(D|Mj,U)在实际计算中，经常用拉普拉斯的渐进展开来近似计算：

(10)

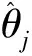
奥克汉因子被用于评估模型Mj鲁棒性，如果模型参数对测量值很敏感并非是好事，这意味着拟合系数一个小的变化就会引起预测值出现一个对应的很大的改变。一个模型的奥克汉因子越高，鲁棒性就越大，模型就越强健，对测量误差的敏感度就越低[8]。

(11)

(12)

(13)

(14)

预测方程的广义公式可以写成如下形式：

(15)

式中：yi为向量y=[Hb,Bt,Bave,Qp,Tf]预测的破坏参数；xj为向量x=[Hd,Hw,Vd,Vw]中控制变量的选择；Pi为模型Mj控制变量的集合。

4个溃口参数通过排列组合形成15个模型种类(表1)。

表1 模型种类列表

4 数据分析

4.1 控制变量与溃口参数的关系研究

见表2。

从表2可以看出，Bave与Hw有较大的相关性(ρ=0.61)，与Vd和Vw次之(ρ大于0.5)，说明溃口的平均宽度与溃口水头的关系较大。同时，溃口水头Hw相比较其他3个参数，溃口顶部宽度Bt与其相关性最大(ρ=0.65)；Hb与Hd(ρ=0.92)和Hw(ρ=0.97)都有很大相关性，说明溃口深度与大坝宽度和溃口水头有密切关系；洪峰泄量Qp则是与溃口水头Hw和溃口容积Vw有相对较大且相同的相关性(ρ=0.66)；对于溃决时间Tf而言，大坝水库容积Vd和溃口容积Vw与其相关性较大(ρ=0.51)。

表2 相关系数表

4个控制变量与溃口参数之间的关系亦可通过散点图得出。图2以Hb为例，Vd、Vw、Hd、Hw的数据进行了标准化处理。

图2中可以看出，Hd和Hw与Hb呈明显的正相关关系，同样验证了溃口深度与大坝宽度和溃口水头有密切关系。

4.2 模型选择

每个候选模型的合理性和奥克汉因子值都可以通过基于贝叶斯推论的模型选择框架获得。图3为Hb加的形式下的预测结果。图3中同时包含只代表模型准确度的大小的确定系数R2和奥克汉因子的对数形式，以便做出比较。

图2 溃口深度Hb与各变量关系图

图3 Hb的模型分析图

从图3中可以看出，模型15具有最大的R2值。然而模型15的奥克汉因子对数值最低，这表明虽然该模型有很高的准确性，拟合误差最小，但是鲁棒性最低。也就是说，模型15对测量值的变化很敏感，不利于预测。模型5不仅有最大R2值，而且奥克汉因子对数值较小，可以作为最优的模型选择。同理，可以找出其他溃口参数的最优模型。

溃口参数相关性最大的变量和最优模型的R2值的关系见表3。从表3中可以看出，具有最大准确度，即R2值最大的模型并不是最理想的。

表3 R2值与相关变量关系

5 结 论

贝叶斯推论近10年在工程中的应用比较广泛，也体现出其优越性。预测方程参数通常使用最小拟合误差作为唯一指标，模型选择过程中只考虑准确度，过度拟合不仅使公式过度复杂，也会导致预测结果不理想。本文运用贝叶斯推论分析了水坝溃口参数与变量之间的关系，验证了模型选择时不能只考虑准确度，导致过度拟合，还应该考虑模型的鲁棒性，最后根据最优模型得出的预测方程对测量值变化较不敏感，更具有可预测性。