关于“小孔成像”的研究
潘志民 金凯文 潘开欣
(1 南京外国语学校,江苏 南京 210008; 2南京迈塔科创教育技术有限公司,江苏 南京 210019)
1 从几何光学看“小孔成像”
光在同种均匀物质中沿直线传播,这是几何光学中的一个基本观点。一直以来,“小孔成像”仅仅作为光的直线传播的实验为大家所共知。
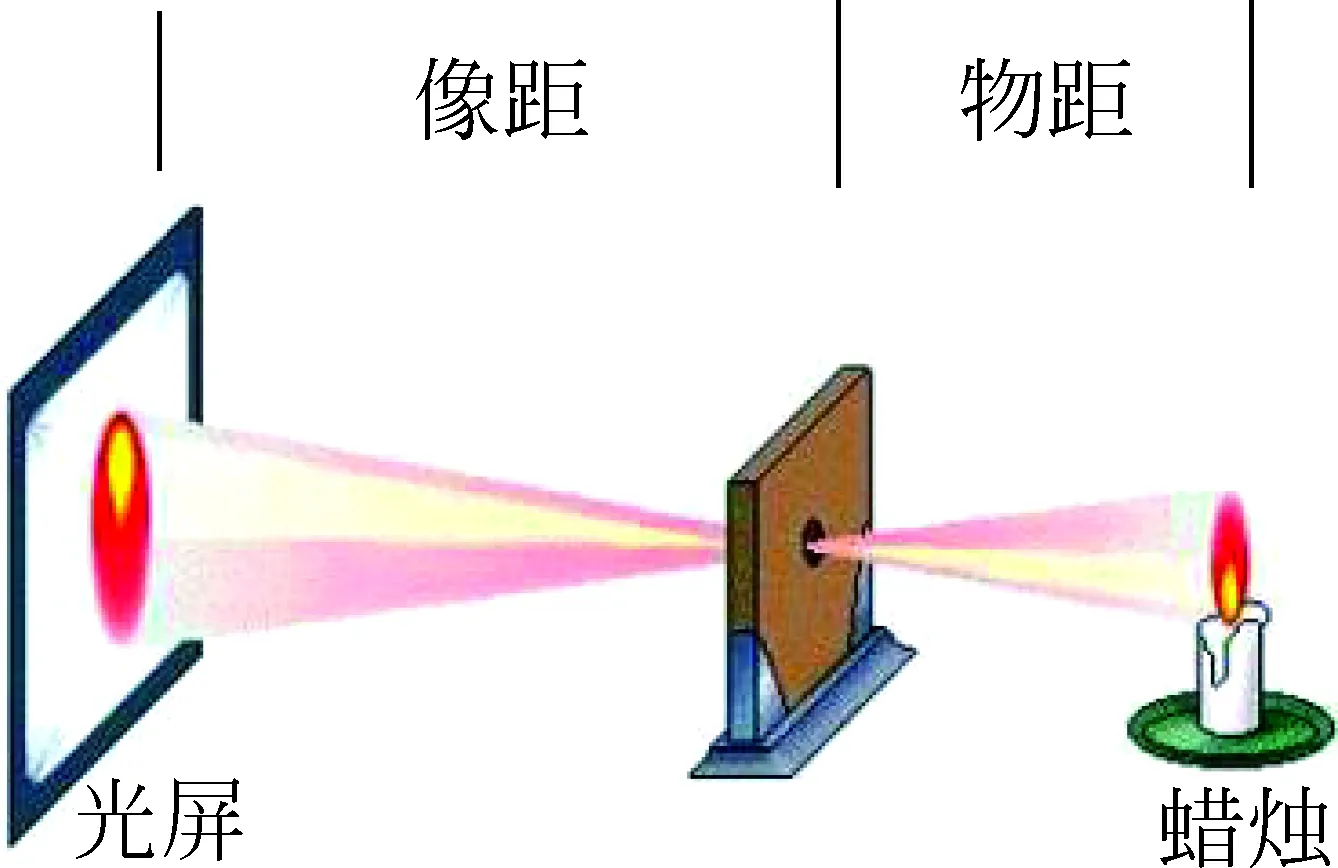
图1 “小孔成像”示意图
查百度百科“小孔成像”的实验结论有:物距越近,像越大且亮度越暗;物距越远,像越小且亮度越亮。像距越近,所成像越小且亮;反之,越大且暗。孔只要够小,它的形状不论是方的、圆的、扁圆的,对像的清晰程度和像的形状都没有影响。
在图1中我们把蜡烛的火焰看成是由许多小发光点组成,每个发光点都向四面八方发射着光。总会有一小束光,笔直地穿过小孔,在白纸上形成一个小光斑。烛焰上的每一个发光点都会在白纸上形成一个对应的光斑,全部光斑在白纸上就组成了一个烛焰的像。
通常认为“小孔成像”成的是倒立的实像,其实严格说来,小孔成像并没有“成像”,“小孔成像”与几何光学中的成像含义截然不同。后者是同心光束经过光学仪器后变换为另一同心光束,若变换所得同心光束是汇聚光束则称为实像,变换所得同心光束是发散光束则称为虚像,成像位置即同心光束之“心”所在位置,它在空间上是一定的,因而人眼可以直接观察物体经过光学仪器所成的像。而“小孔成像”的“像”不是同心光束之间的变换,它只是小孔选择物体表面上各物点发出的各种光线中的各一条(由物点至小孔的直线所决定),它需要投射到一个平面屏上,光点代表了物点在物体上的相对位置和亮度,人眼才能观察到像(经过了人脑的综合作用),像的大小随平面屏的位置而变化,平面屏离小孔越远小孔成像就越大。
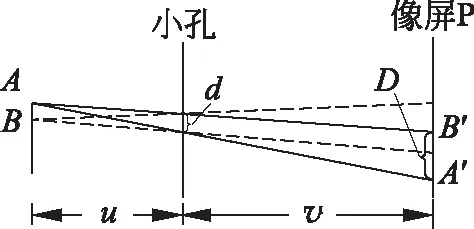
图2 “小孔成像”的几何关系
小孔的尺度会导致物平面上的点在像平面成像时产生模糊,原因在于小孔有一定的几何尺寸, 并非几何点, 所以物点发出的光线经过小孔后就形成了扩散的光束, 落在光屏上就变成了光斑(像斑) 而不是光点。光斑间发生相互重叠, 就产生了像的失真。若当像平面两个光斑之间恰好没有重叠(即恰好相切)时,可以视为能够分辨。在图2中,设物距为u,像距为v,小孔直径为d,某点(A或B)通过小孔在像屏P上形成的光斑(A′或B′)直径为D,则有
(1)
若物平面上相距δH的两个点,在像平面上成的光斑恰好没有交叠,其对应像斑中央在像平面上的距离为δH1,有
δH1≈D
(2)
在图中存在几何关系
(3)
综合以上诸式,有
(4)
据此可以得出,“小孔成像”可以分辨的最小距离δH与小孔直径d成正比,与物到小孔距离u呈正相关关系,与小孔到屏幕距离v呈负相关关系。“小孔成像”中从几何光学看,小孔越小成像会越清晰,但实际上不会,原因是孔径太小成像光能就会减少,从而影响成像的亮度,导致不清晰。
2 从波动光学看“小孔成像”
从波动光学的角度来看,光波是波长极短(几百纳米)的电磁波。在同一种介质中,光波的波线为直线,考虑短波长近似(忽略衍射),光波束可以用光线来表示。通常被观测物体的线度远远大于光波波长,若小孔线度满足远远大于光波波长,而且还要远小于物体的线度,物体表面上各点(物点)发出(或反射出)的光线经过小孔屏后,投射到一个平面承接屏上,平面屏上投射光的分布将体现出物体的轮廓,这就是所谓“小孔成像”。
若小孔线度不满足远远大于光波波长,由于光具有波动性,衍射会对小孔成像产生影响,几何光斑的边界处不再亮暗分明。人眼观察小孔成像,不仅受到像质(大小、形状、色彩等)的影响,还会受到成像亮度(成像光强)的影响,成像太暗便观察不清。也就是说小孔孔径的变化,不仅影响像质,还影响亮度。
2.1 小孔衍射对成像分辨率的影响
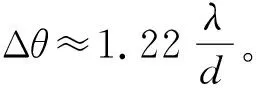
(5)
作出最小分辨距离δH与小孔直径d关系的趋势示意图如图3所示。从图中我们可以看到:当孔径较大的时候,几何光学对分辨率的影响占主要地位;当孔径较小的时候,主要的限制因素则为衍射。图中的“总体效果”综合两种因素定性地反映出总体变化趋势,可知当小孔直径取适当值时,有最小分辨距离,此时成像的分辨能力最强。
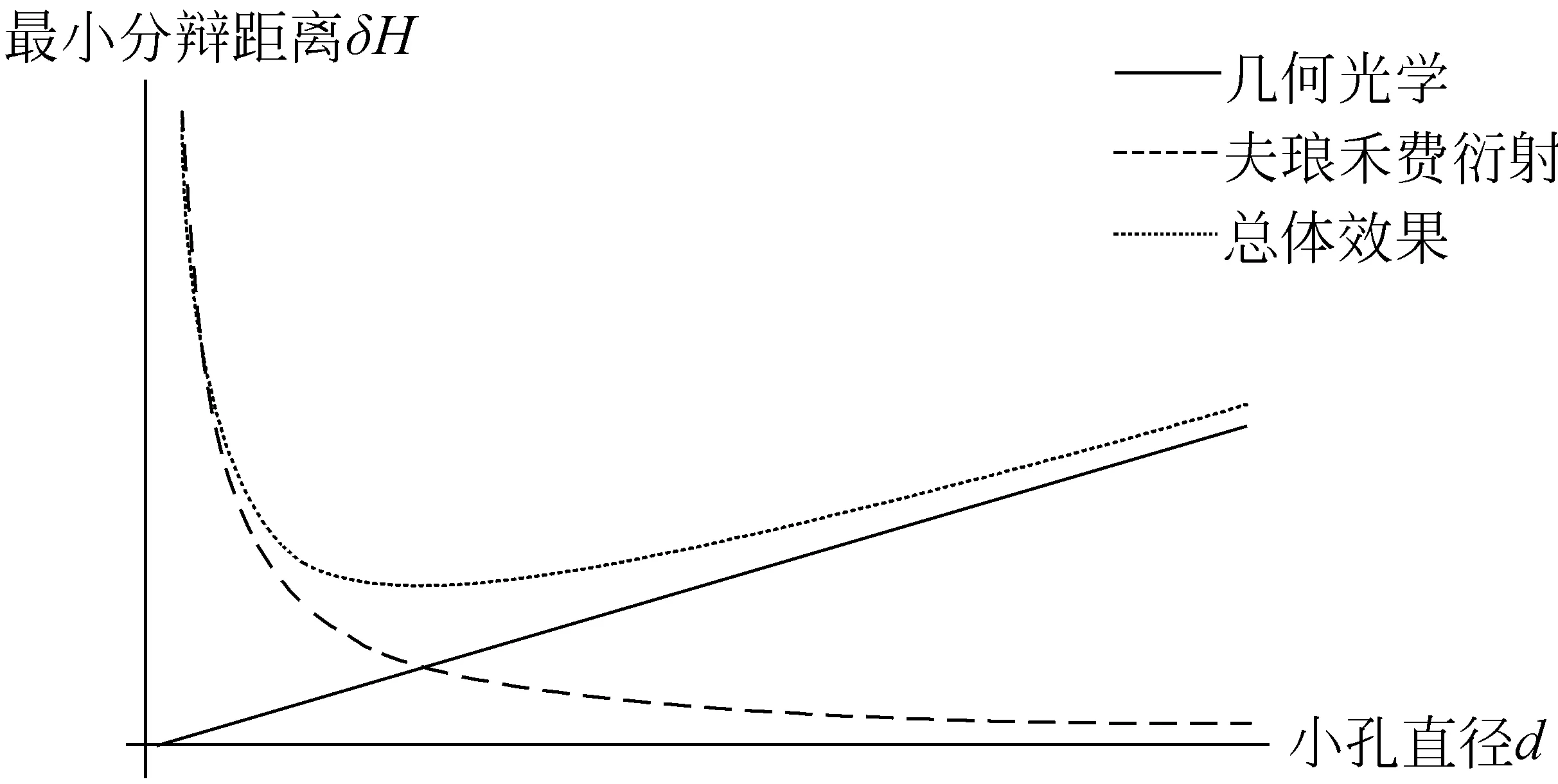
图3 最小分辨距离与小孔直径关系示意图
2.2 孔径、物距和像距等参数对成像亮度的影响
被观测物体(等效为光源)均匀发光时,其光通量Φ恒定。各等效光源点到小孔的方向随物距u变化,物体相对于物距很小时,可忽略方向的变化,各源点到小孔的发光强度均可视为一常量。记物体在小孔处的发光强度为I,则像方的光通量为
(6)
式中,d为小孔直径;ΔΩ为小孔对某源点的方位角,在方位角的计算中运用了小角近似。
我们实验中使用圆形物体正对小孔放置,设其直径为H、像的尺寸为H1,在“小孔成像”中有几何关系
(7)
像的面积为
(8)
则在光屏(毛玻璃)上所得像的照度为
(9)
光屏上像的光亮度正比于此照度。此式说明,对于确定的被观测物体H一定,像的亮度与小孔直径d呈正相关关系,与小孔到屏幕距离v呈负相关关系;还表明像的光亮度与物距无关,这一点与百度百科中“物距越近,像越大且亮度越暗;物距越远,像越小且亮度越亮”的结论完全不同。
那么,物距、像距和孔径与成像亮度、清晰度有何关系,以及小孔直径取何值时,小孔成像的分辨能力最强,下面通过实验来定量研究这些因素对小孔成像的影响。
3 “小孔成像”的现代物理实验研究
3.1 研究孔径、物距和像距对成像清晰度的影响
设物的尺度H,像的尺度H1,小孔直径d,小孔屏到物的距离u,小孔屏距离像屏v。从实验上得出它们的相对关系为何值(或者何范围)时,成像效果最佳。也就是说,通过实验结果能知道欲使成像清晰,小孔是大一些好呢,还是小一些好?物距和像距是近一些好还是远一些好?
3.1.1 实验研究孔径对成像清晰度的影响
实验中使用白炽灯作为光源,用于被观测圆形物体的直径为H=4mm。首先将物距u、像距v均控制在6cm,改变孔径d大小,用CMOS照相系统(包含CMOS相机,0.6倍远心镜头)对小孔的成像进行采集,以下是其中对孔径100μm、200μm、500μm等3种小孔的成像的采集结果:
由图4可以看到,孔径d=200μm小孔的成像质量最佳,边缘的亮度突变最为显著,d=100μm时由于衍射效应导致边缘模糊,而d=500μm时由于孔径过大导致边缘模糊。故,以下实验均采用孔径d=200μm小孔。
3.1.2 研究物距和像距对成像大小及清晰度的影响
现控制小孔直径d=200μm,实验中仍使用白炽灯作为光源,被观测物体直径H=4mm。控制曝光时间和增益为恒定值,改变物距u和像距v,测量其对成像大小及清晰程度的影响。以下为采集到的部分图片:
对采集到的图片进行比对,可以发现物、像距对像边缘清晰度的影响较小。那么可以认为物、像距对成像清晰程度的影响主要在于对像尺寸和亮度的影响。我们使用Tracker软件对图片的像尺寸H1和亮度B进行分析,得到物距u、像距v和像尺寸H1、亮度B关系曲线如下:
由图6至图9可见像尺寸(大小)与像距呈正相关,而亮度与像距呈负相关;像尺寸与物距呈负相关,而像亮度在物距变化时保持了一个相对恒定的值。
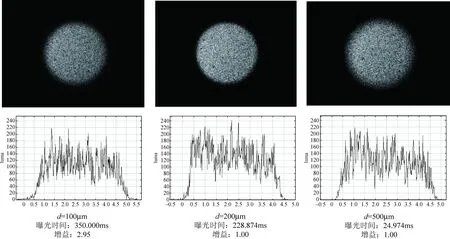
图4 3种不同孔径小孔成像实验采集结果

图5 小孔成像大小及清晰程度与物距u、像距v的关系
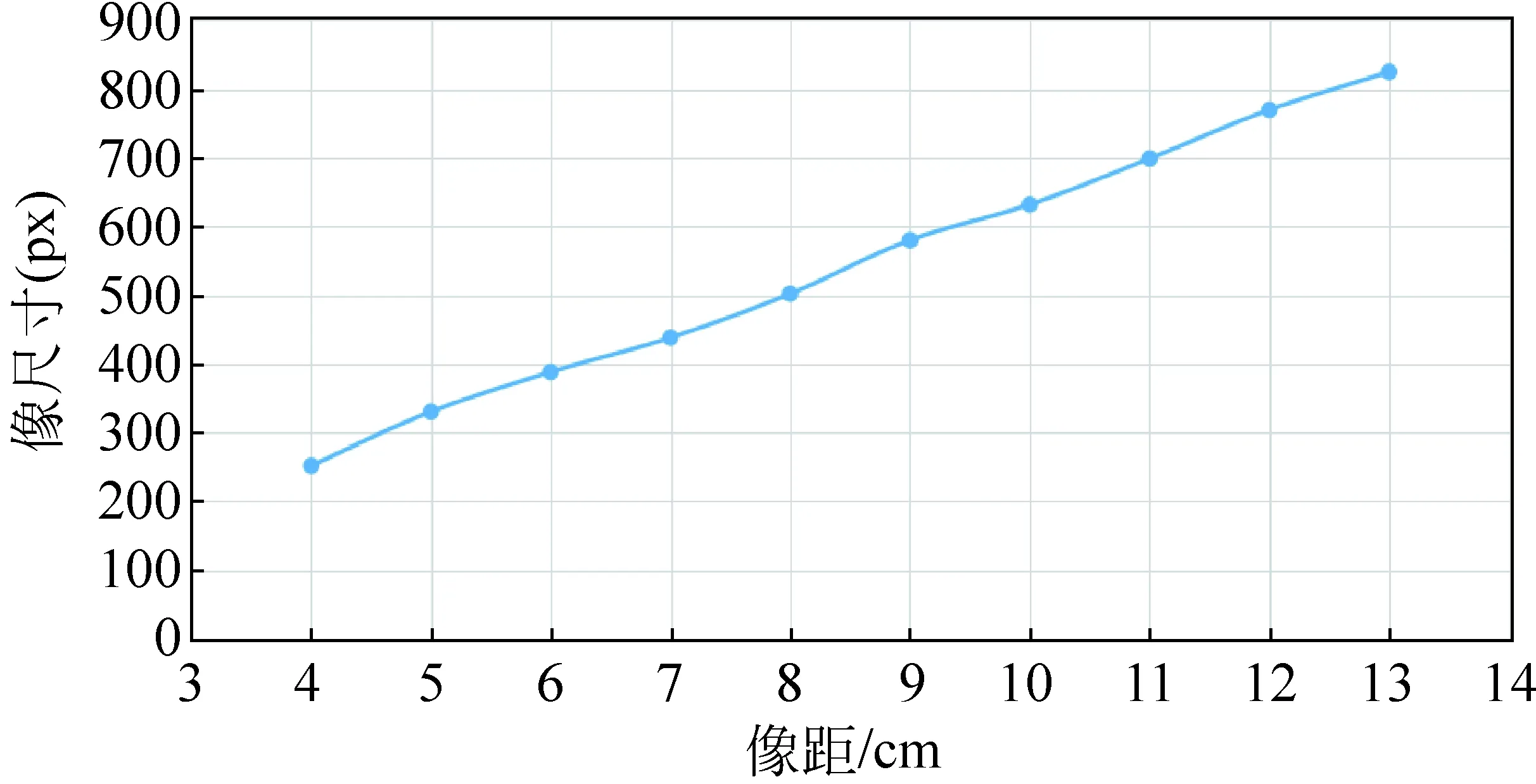
图6 像尺寸H1—像距v曲线(物距u=6cm)
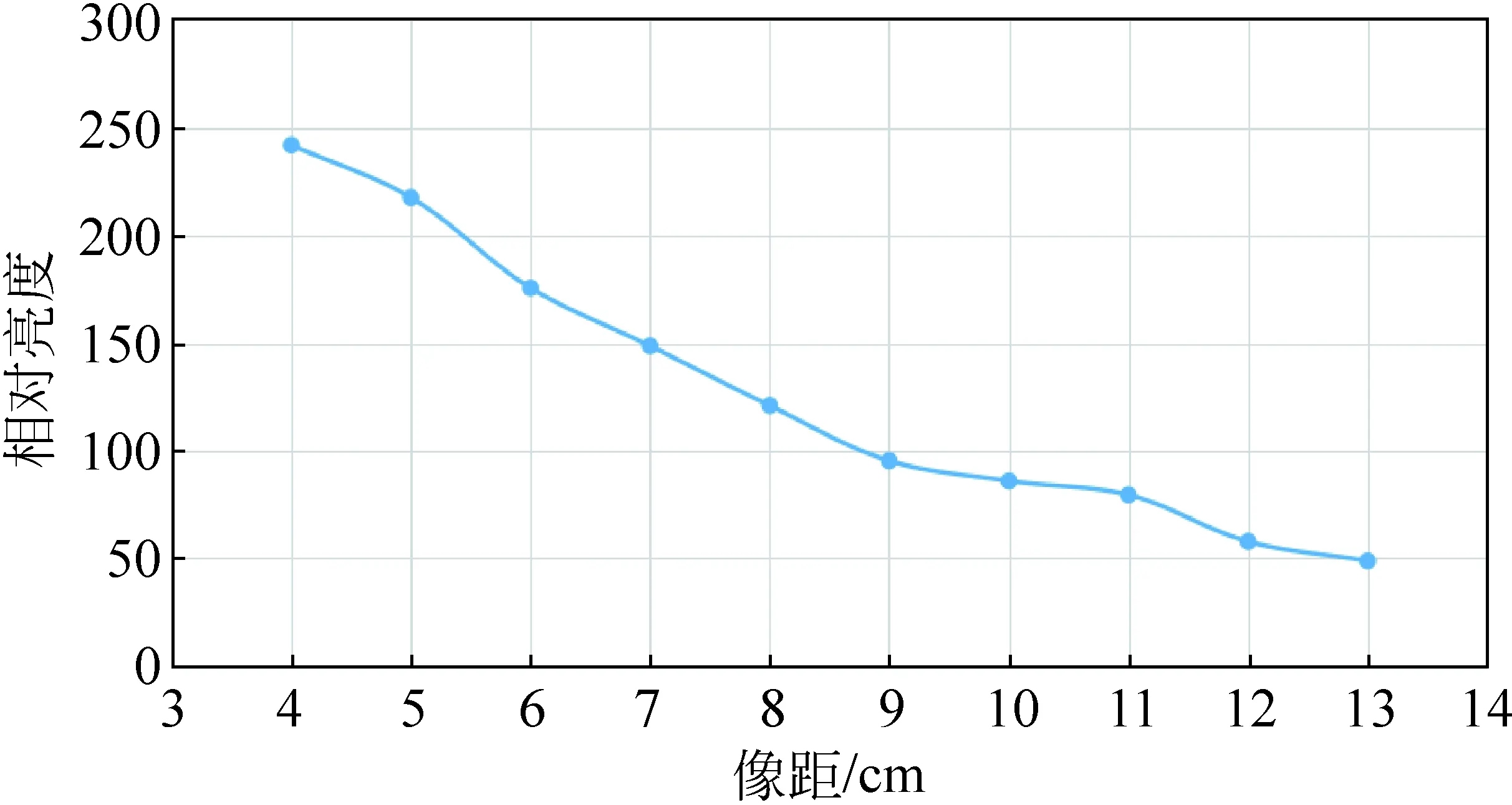
图7 亮度B—像距v曲线(物距u=6cm)
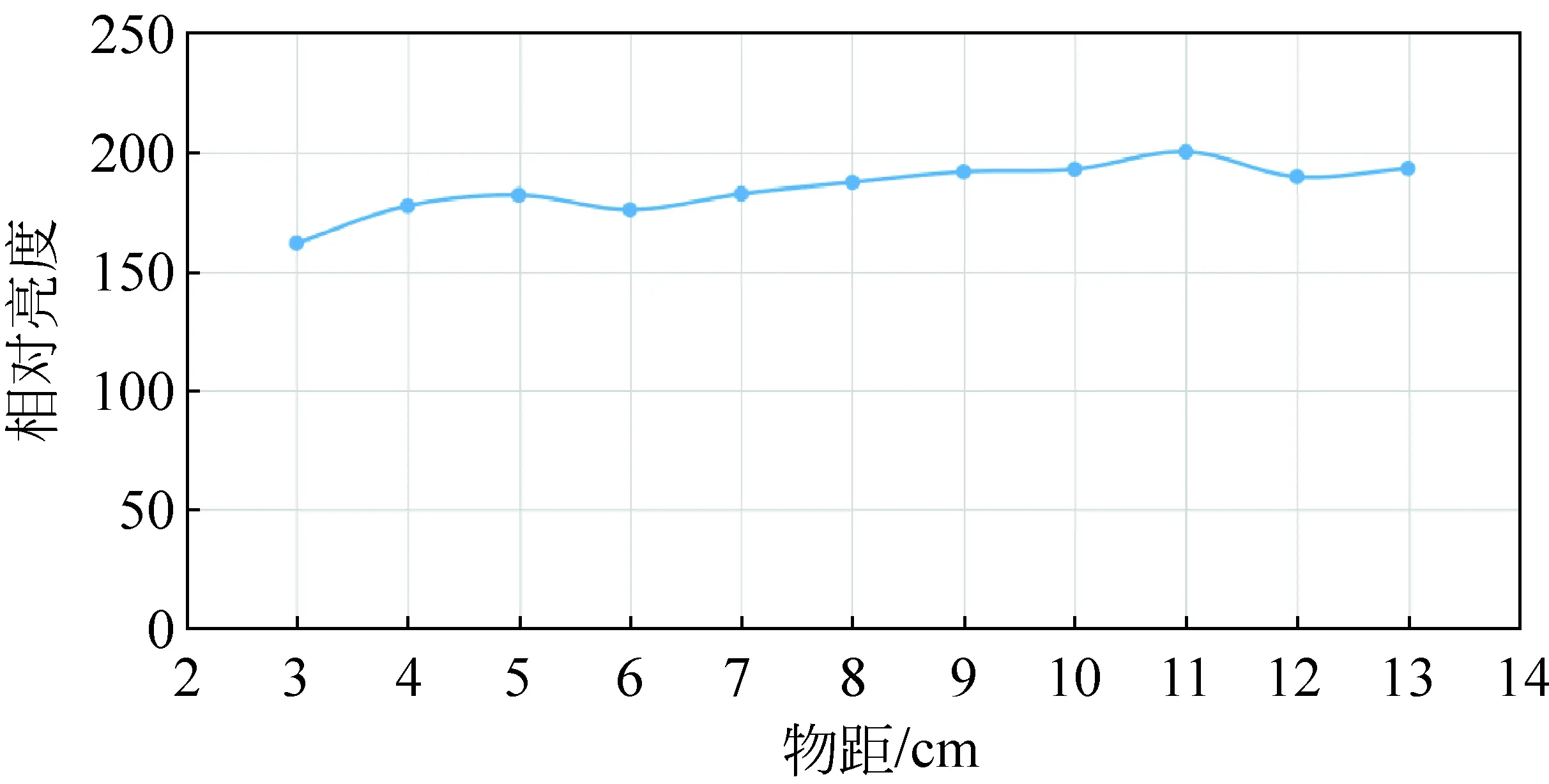
图9 亮度B—物距曲线u(像距v=6cm)
要想使成像更清晰,必须保证像具有足够大的尺寸和足够高的亮度。对于像距而言,为使成像足够大,像距不宜过小,而同时为使亮度足够高,像距不宜过大。对于物距而言,由于物距不影响成像的亮度,故可以缩小物距以使成像尺寸增大至图像采集设备的采集极限。
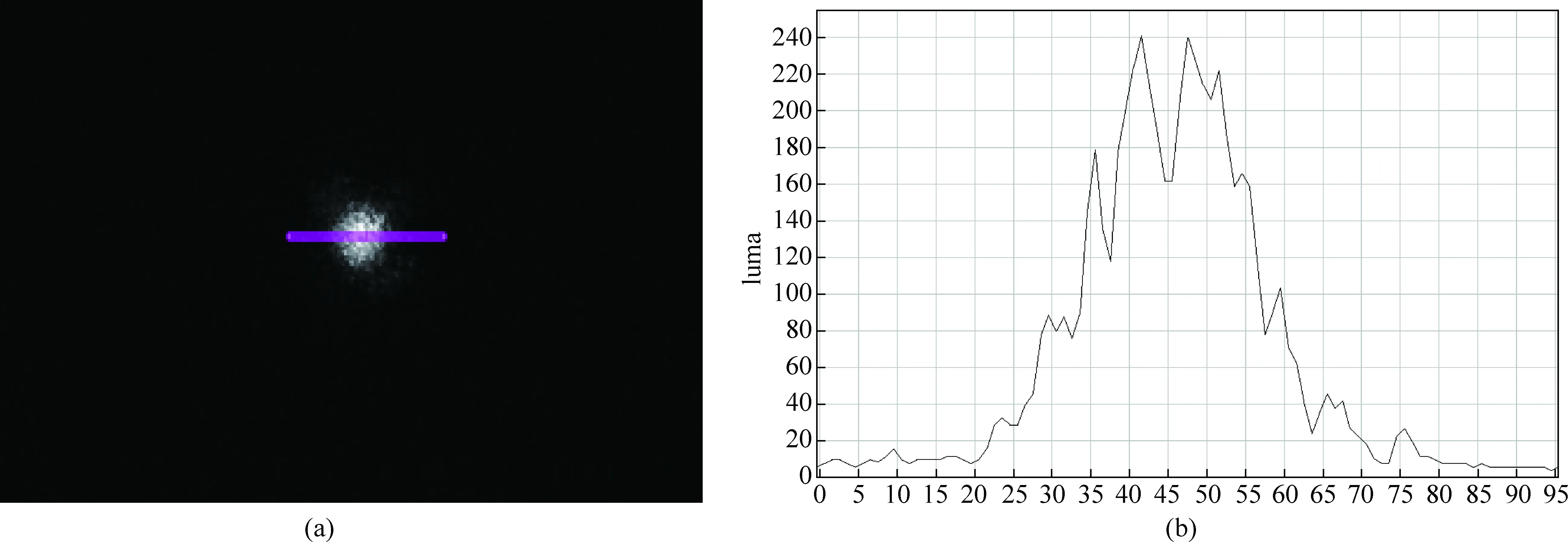
图11
3.2 “小孔成像”分辨本领的实验研究
首先使用直径100μm的针孔作为物点,使用d=200μm小孔屏用于成像,控制物距u和像距v均为6cm,图像采集设备得到图像如图10所示。

图 10
使用Tracker软件对图11(a)中划线部分的亮度进行分析,得相对亮度曲线如图11(b)。
以最大亮度值的一半作为光斑的边缘,可以得到光斑的直径约为22个像素。根据所用相机(单个像素大小:5.86*5.86μm)以及远心镜头的参数(0.6倍),可以求得光屏上的成像直径约为215μm。
由于100μm的针孔相对于成像用的d=200μm小孔来说不够小,所以我们接下来使用分辨率板。将分辨率板置于光源前,控制物距u和像距v均为6cm,使用d=200μm的小孔进行成像实验,以下为得到的部分图像(图12)(图中数字X代表黑条纹的间距为δH=1/(2*X)mm):
可以看到,条纹间距δH在0.18mm(1/5.6)以上时,依然可以较清晰的分辨,而在0.14mm(1/7.2)及0.12mm(1/8.0)时已经较难分辨,当条纹间距小于0.11mm(1/9.0)时已然完全无法分辨。
如果我们取δH=0.20mm(1/5.0)为能清晰分辨,恰好是由式(4)代入数据后算出结果的一半。这里固然有衍射的因素,更主要应该是我们推导式(4)要求的条件过高所致。不妨将其修改为“当像平面两个光斑中央间的距离等于其半径时,可以视为恰好能够分辨。”则式(2)变为:δH1≈D/2,相应式(4)修正为
(10)
将此式变形可得
(11)
实验中在物距u和像距v确定条件下,满足一定的分辨率(最小分辨距离δH)要求,此式可作为在衍射可忽略时选择“小孔成像”合适孔径d的经验公式。
3.3 实验研究“小孔成像”视场范围的限制条件

图 12
在这部分实验中,我们用小孔点阵代表物点,经过小孔成像后,看它们的相对位置是否与物点一致,它们的相对亮度是否与物点的一致,即它能够得到轮廓逼真的像。通过实验得到小孔成像视场范围的限制条件。
现使用间距为2mm,直径为0.5mm的小孔点阵置于光源前,控制物距u和像距v为6cm,使用d=200μm小孔成像,得到部分点的图像如图13所示。
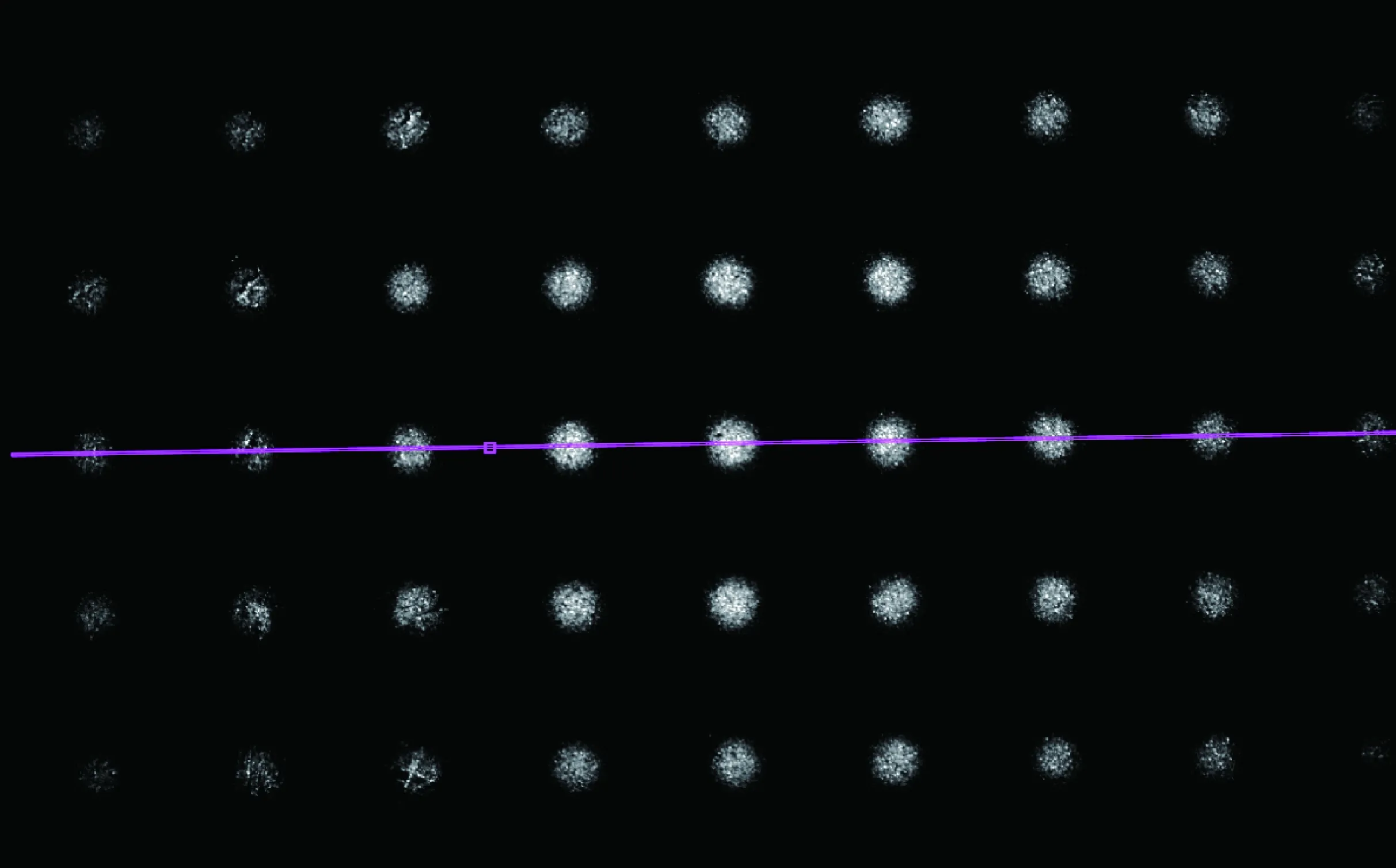
图 13
使用Tracker软件对图13中光斑中心的距离进行测量,可以发现距离基本一致,说明小孔成像对发光物体的形状还原得很好,但可以很明显地发现,图中各点的亮度明显不同,而实际物体亮度应是均匀的。
现采集图13中划出的水平线段的亮度值,得到如下曲线(见图14)。
可以看到,对于左数第一个峰,亮度峰值已经衰减到最亮点亮度峰值的一半左右,而根据点阵参数和物距u可以求得,该点偏离主轴的偏转角仅为7.59°。故可以推测,对于尺寸较大的物体,如果不对物距加以控制,小孔系统所成的像将会在亮度上严重失真。
说明在做“小孔成像”实验时,被观测物体当置于小孔屏的正前方,且物体对小孔的张角不宜过大。
4 结语与致谢
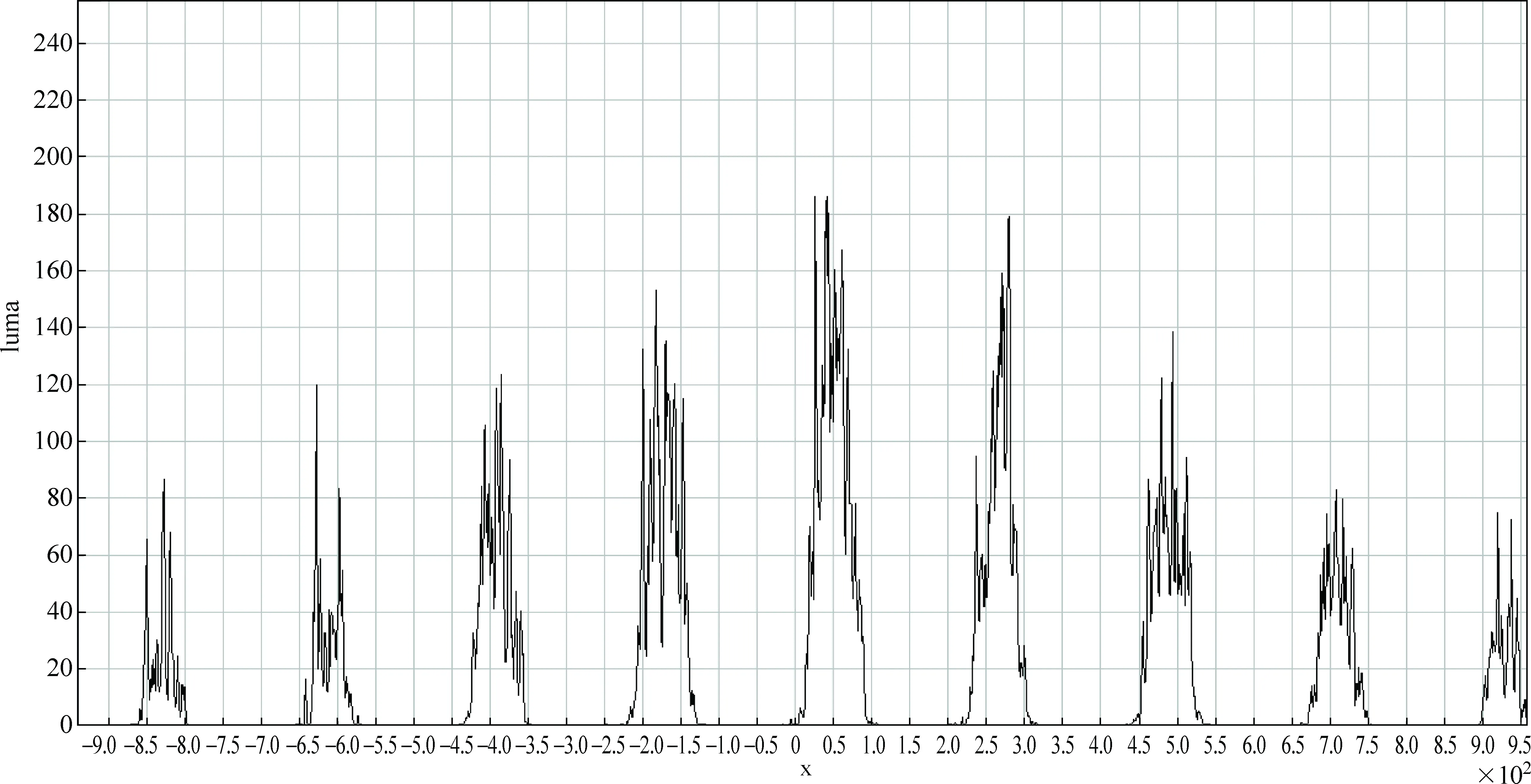
图 14
一直以来,小孔成像仅仅作为光的直线传播的实验为大家所共知,而涉及小孔成像问题的深入研究,包括理论研究和实验研究,未见到有相关的报道。本文为作者在指导学生研究第30届国际青年物理学家竞赛(IYPT2017)第3题的基础上形成,题目要求设计用小孔光阑替代目镜,自制出简易的单透镜望远镜。出于兴趣和需要,我们先从几何光学和波动光学的理论层面做了关于小孔成像问题的深入研究,进而使用现代光学实验技术并借助于ToupView和Tracker等计算机软件对实验数据进行了详细的分析。从而得到了一般性结论,发现理论和实验具有良好的自洽性。
小孔成像的分辨率、像的大小和亮度均会影响我们观察小孔成像清晰程度的主观感觉。具体来说,本文研究得到的结论有:
(1) 物距和像距影响成像大小:物距越小,像距越大,成像越大。
(2) 对于孔径,从几何光学的角度是孔径越小成像越清晰(不考虑亮度影响),从波动光学的角度是孔越小,衍射越明显,成像越模糊。理论和实验均表明:当小孔直径取适当值时,有最小分辨距离,边缘的亮度突变最为显著,此时成像的分辨能力最强,成像质量最佳。
(3) 孔径、物距和像距均会影响成像亮度;像距增大,成像亮度减弱;物距变化,成像亮度变化不明显;小孔孔径在一定范围内增大,成像亮度会增加。
(4)小孔成像对发光物体的形状还原得很好,可以很明显的发现,远离成像中心亮度明显减弱,而实际物体亮度应是均匀的,小孔成像具有边缘模糊化的趋势。
我们把以上研究结果引入望远镜系统,指导学生自制单透镜望远镜,比较好地完成了IYPT2017第3题,使得研究更加深入与实际。
本文在理论研究上尽管给出了分辨率与孔径、物距和像距的经验公式,但略显粗糙,希望进一步依据物理光学理论精确推导出分辨率与孔径、物距和像距的函数关系,作为指导实验的理论根据。在实验研究方面,需要提高测量精度,也可以使用相干光源进一步研究,希望能精确测出在不同物距和像距条件下最佳成像孔径,以期给成像技术应用有更好的借鉴作用。另一方面,由于“小孔成像”不是真正的物理成像,不太能被方便地处理和利用,加上小孔通光孔径小,能量利用率低,因此“小孔成像”未能在成像科学技术中被广泛利用。但从自然科学的角度,对小孔成像问题作深入研究是很有意义的,同时本文所做研究对指导中学物理教学以及在照相机和摄影机等成像科学技术中领域也有一定的借鉴意义。
最后在此感谢清华大学路俊岭教授给予的理论指导和研究建议;感谢南京迈塔光电Metalab创新实验基地给予的实验支持,感谢雎长城博士提供宝贵意见。
■

