采煤机摇臂行星轮齿根应力分析
天地科技股份有限公司上海分公司 上海 200030
1 研究背景
煤炭是我国的重要能源,煤炭消耗占整个国家能源消耗的67%左右。滚筒采煤机是煤矿综合开采生产的重要设备,对“一井一面”千万吨级集约化煤矿的建设起着关键作用。随着采矿技术的发展,重型采煤机得到应用,总装机功率已接近3 000 kW,单摇臂截割功率达到1 100 kW。受煤矿综合开采工作面设备配套及煤矿安全规程要求的限制,采煤机摇臂传动系统设计普遍采用直齿加行星传动的结构,螺旋滚筒安装于行星减速器上,可见摇臂行星减速机构首当其冲地承受着采煤过程的载荷。由于工况恶劣,摇臂,特别是摇臂行星减速机构时常受到冲击载荷,因此在设计摇臂齿轮时,首先要保证齿面硬度和接触疲劳强度,多选用优质渗碳合金钢作为齿轮材料。但这样做造成了齿根的弯曲疲劳强度相对较低,容易出现断齿失效现象[1-2],如图1所示。
2 摇臂行星轮齿根应力分析
摇臂行星减速机构设计时,基本都采用薄壁行星轮和短圆柱滚子轴承的结构形式。这一结构特点造成行星轮工作时,其内壁与滚子轴承的接触应力对齿根弯曲应力有较大的影响。
根据标准直齿圆柱齿轮传动的受力分析,将标准直齿圆柱齿轮传动受力分析公式中的标准齿轮分度圆直径替换为变位齿轮的节圆直径d1',压力角替换为啮合角α'[3],可以计算出作用在行星轮系中行星轮上的圆周力Ft2、径向力Fr2及法向力Fn2,它们与作用在行星轮中太阳轮上的圆周力Ft1、径向力Fr1及法向力Fn1的关系如下:
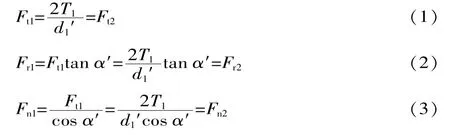
式中:T1为作用在太阳轮上的转矩。

▲图1 摇臂齿轮齿根断齿失效情况
行星轮的径向力和圆周力与相啮合太阳轮或内齿圈的径向力和圆周力大小相等,方向相反。在确定力的方向时应注意:太阳轮与行星轮啮合时,太阳轮上圆周力Ft1的方向与力作用点的圆周速度方向相反,而行星轮上圆周力Ft2的方向则与力作用点的圆周速度方向相同;内齿圈与行星轮啮合时,行星轮上圆周力Ft2的方向与力作用点的圆周速度方向相反,内齿圈上圆周力的方向则与力作用点的圆周速度方向相同;齿轮径向力的方向,对外齿轮而言由力的作用点指向轮心,对内齿轮而言则背离轮心。
摇臂在恶劣工况下高强度工作,行星轮经常有断齿失效现象发生。为了防止轮齿疲劳折断,在设计时齿根弯曲应力σF不得大于自身许用应力[σF],并留有足够的安全因数。
一般而言,根据齿轮传动理论,齿根弯曲应力为:

式中:K为由使用因数、动载荷因数、齿间载荷分配因数及齿向载荷分布因数等耦合的载荷综合因数;Ft为圆周力;B为行星轮齿宽;m为行星轮模数;YF为齿形因数;YSa为应力矫正因数。
应力矫正因数的引入,解决了齿根圆角造成的集中应力对齿根应力影响不易计算的问题[4]。
由于行星轮内孔处和滚动轴承外圈之间存在配合关系,由此必然会在齿根处产生弯曲应力。齿根处的弯曲应力为两外载荷产生的弯曲应力的合力,即行星轮与太阳轮啮合时在行星轮齿根处产生的弯曲应力,以及行星轮与滚动轴承外圈配合时在行星轮齿根处产生的应力的合力[5]。
由弹塑性力学厚壁圆筒理论可得:
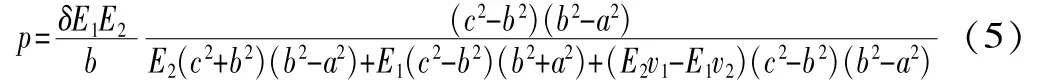
式中:a为滚动轴承外圈内孔半径;b为行星轮的内孔半径,也即滚动轴承外圈外径;c为圆筒的外径;E1为滚动轴承外圈材料的弹性模量;E2为行星轮材料的弹性模量;v1为滚动轴承外圈材料的泊松比;v2为行星轮材料的泊松比;δ为滚动轴承外圈与行星轮的过盈量;p为行星轮内孔与滚动轴承外圈配合处的压力。
受齿轮的影响,按式(5)计算行星轮弯曲应力时,不能完全根据实体厚壁圆筒取c值,而可以按分度圆半径r取c值,即c=r。
滚筒采煤机摇臂行星轮齿根处应力σ为行星轮与轴承过盈配合的应力σF,以及行星轮转动时与太阳轮啮合产生的弯曲应力σθ的合力,可以表示为:
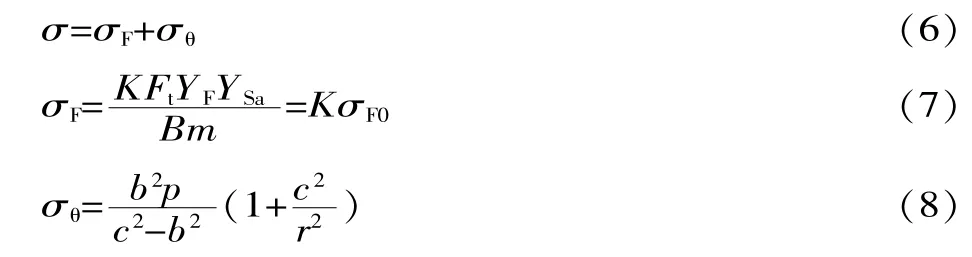
式中:σF0为齿根基本应力。
由此,可得:
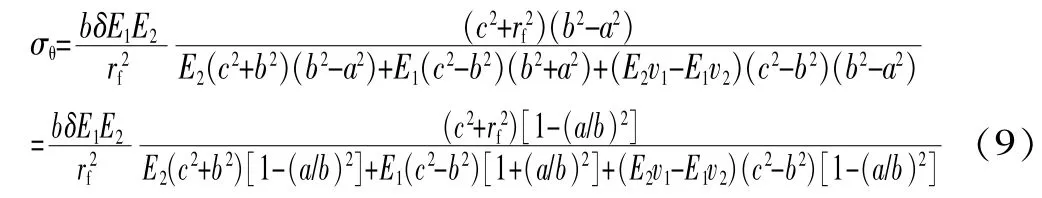
式中:rf为齿根圆半径。
3 减小齿根应力的方法研究
由上述分析可知,影响行星轮齿根弯曲应力的因素有装配过盈量δ、行星轮内孔半径b、滚动轴承外圈内孔半径a。行星轮与轴承过盈装配时,可通过改变δ、a、b来减小行星轮齿根弯曲应力。
3.1 σθ与δ的关系
当a、b不变时,应用Matlab软件模拟分析,得到行星轮与太阳轮啮合时在齿根处产生的弯曲应力σθ与δ的关系,如图2所示。可见σθ与δ成线性关系,σθ随δ的增大而增大,所以要减小齿根弯曲应力,可以通过减小δ来实现。
3.2 σθ与a的关系
当齿轮模数m,以及δ和b不变时,应用Matlab软件模拟分析,得到行星轮与太阳轮啮合时σθ与a/b的关系,如图3所示。可见σθ随着a/b,即a的增大而减小,所以要减小σθ,可以选择a大的滚动轴承。
3.3 有限元分析
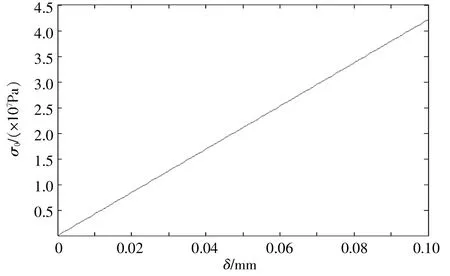
▲图2 σθ与δ关系曲线

▲图3 σθ与a/b关系曲线
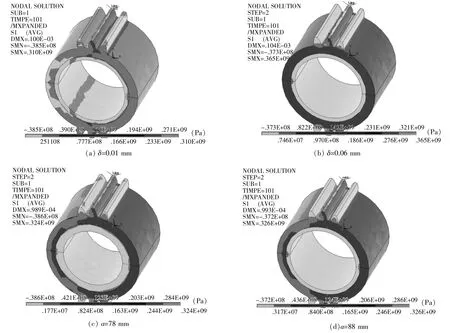
▲图4 齿根弯曲应力云图
如图4所示,为了验证上述分析的正确性,笔者分别对δ和不同a的行星轮齿根弯曲应力进行有限元仿真计算[6~10],得到应力云图。
通过对有限元仿真结果分析整理,得到δ、a与σθ的关系,如图5所示。可见δ、a与σθ近似成正比关系。
通过上述分析可以得出,当确定滚动轴承型号,即参数滚动轴承外圈内孔半径确定之后,可以通过减小过盈量来减小齿根弯曲应力。当行星轮内孔确定,即滚动轴承外圈外径确定之后,可以选择外圈内孔半径大的滚动轴承来减小齿根弯曲应力。
4 结语
笔者通过对滚筒采煤机摇臂行星减速机构进行弯曲应力分析,得到了在行星轮齿根处产生弯曲应力的复合函数。
通过Matable模拟分析,得出太阳轮与行星轮啮合时行星轮齿根弯曲应力与装配过盈量、滚动轴承外圈内孔半径的关系。
通过分析,确认了影响行星轮齿根弯曲应力的关键因素,并提出了相应减小弯曲应力的方法,对采煤机摇臂行星减速机构的设计具有一定的指导意义。
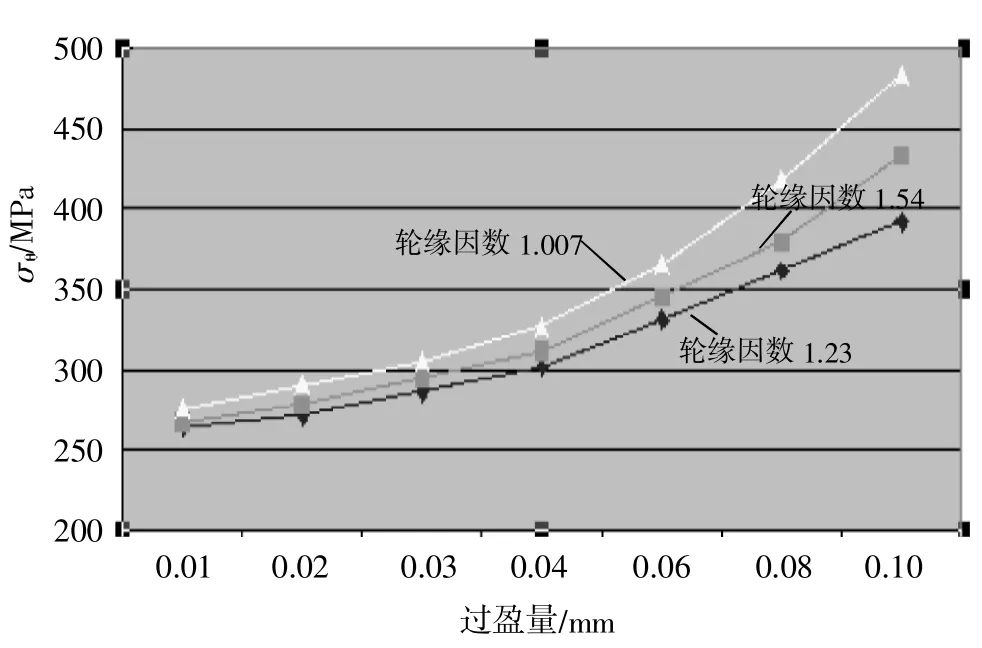
▲图5 δ、a与σθ关系曲线

