基于价格预测的水运工程材料价格决策研究

姚卓宏

湖南省交通规划勘察设计院有限公司，湖南长沙 410005

1 水运工程投标报价现状

在水运工程投标过程中，一般是采用现在的市场材料价格进行综合单价组价，再加上一个市场材料价格上涨的风险费用。目前风险费用一般是通过主观预测确定的，需要一种科学的方法来避免材料价格上涨带来的不利影响。

2 水运工程材料的动态价格决策模型

对材料价格变化应采用客观科学方法对其做出更加准确的预测，同时还应将预测得到的材料价格和施工组织设计中的材料需求供应计划结合，通过分阶段计算出符合施工进度计划的材料平均价格，即采用动态价格决策模型来对水运工程建设材料价格作出更加准确的估计，如图1所示。

2.1 市场价格的变权重组合预测模型

水运工程材料价格是一个较复杂的变量，影响因素多，若将灰色系统与神经网络结合起来，构成组合预测模型，能够充分发挥各单项预测方法的优势。

为了能够更好地适应预测环境的变化，选取变权重组合预测模型来进行预测。设对于同一个预测问题，有n种预测方法f1，f2，…，fn，则由这n种预测方法组成的组合预测模型为：

式中：y（t）—变权重组合模型在t时刻的预测值；gi（t）—第i种模型在t时刻的权重系数 ；fi（t）—第i种模型在t时刻的预测值。

设eit、et分别为第i种模型和变权重组合模型在t时刻的预测误差，则相应的表达式为：

式中：Y（t）—在t时刻的实际观察值。

确定组合预测变权重系数的方法是使样本点处组合预测的误差最小，同时还要满足权重系数自身的要求，因此可得到如下组合模型的优化模型[1]：

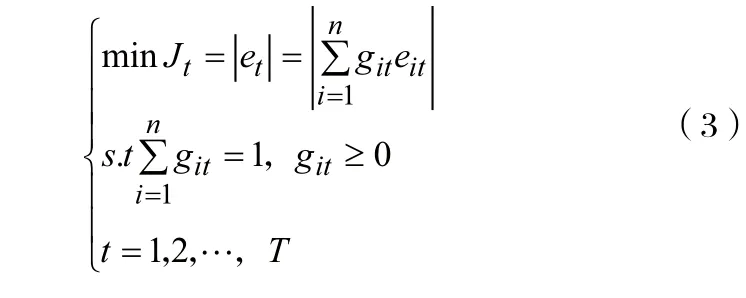
（1）对于在t时刻的样本点，各种单一的预测模型均有eit≥0（或者eit≤0）的情况。假设此时第p种预测模型的误差最小，∣ept∣=min∣eit∣，则模型的解：

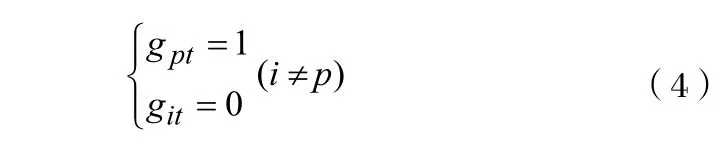
（2）对于在t时刻的样本点，各种单一预测模型的误差中有一部分eit≥0，另一部分eit＜0的情况。假设此时所有预测误差为非负数的模型中第P1种模型预测误差的绝对值最小；所有预测误差为负数的模型中第P2种模型预测误差的绝对值最小。此种情况下模型的解为[2]：

在进行预测时，预测时刻t（t=r+1，r+2，…，r+z）处的各个预测模型的权重系数，可以按照下式计算求得。

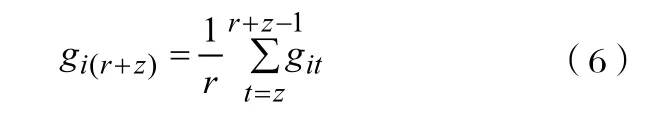
式中：r—预测时所选基础样本点的个数。

2.2 材料需求供应计划

在编制水运工程施工组织设计时，根据材料需求量和施工进度计划编制材料供应计划。

2.3 材料平均价格的确定

根据动态价格决策模型，如水运工程从开工之日起到工程竣工之日止，工期为n期，则该水运工程第k（k=1，2，3，…）种材料平价格确定的具体步骤如下：

（1）根据施工组织设计中资源需求计划，可得到每期第k种材料的需要量为vi，则V=（v1，v2，…，vn）；

（2）根据市场价格预测，可得到每期第k种材料的预测价格为pi，其中i=（1,2，…，n）则P=（p1，p2，…，pn）T；

（3）该水运工程预测的第k种材料总的费用为：C=V×P，第k种材料的平均价格为：

3 实例应用分析

以湖南某码头工程为例，该工程建设工期为1年，开工日期为2010年10月。

3.1 水运工程材料价格相关数据

考虑到水运工程建设对钢筋需求量大，下面以螺纹钢为例进行分析。通过对该码头工程编制施工组织设计，可得到该码头工程对螺纹钢的需求供应计划，如下：2010第4季度490t、2011第1季度390t、2011第2季度115t、2011第3季度89t。

从2003第1季度到2011第3季度（共35期）的螺纹钢价格数据如下（单位：元/t）：第1期到第10期：2872、3396、3396、3899、4431、3764、3935、3947、3961、3613；第11期到第20期：3293、3154、3210、3360、3286、3393、3716、3761、4154、4863 ；第21期到第30期 ：5252、5795、5565、4273、4129、3882、4326、4099、4201、4552 ；第31期到第35期 ：4430、4766、5090、5405、5298。

3.2 水运工程材料价格预测分析

3.2.1 预测模型预测

分别利用GM（1,1）模型、BP神经网络模型和变权重组合模型进行预测，结果见表1。

表1 2010年第4季度到2011年第3季度的价格预测值（元/t）

3.3 水运工程材料平均价格的确定

由表1可知该码头工程对螺纹钢HRB 335（Φ10以外）各季度的需求供应计划为V=（490，390，115，89），由表4可知螺纹钢HRB 335（Φ10以外）各季度的预测价格为P=（4699.69，5142.57，5375.17，5240.07）T，将P、V结合代入动态价格决策模型，得到C=V×P=5392962.18，进而求出螺纹钢HRB 335（Φ10以外）的平均价格为

4 结语

本文综合考虑了材料未来价格变化和需求供应计划对整个水运工程建设过程中材料费用的影响，在此基础上提出了动态价格决策模型，并通过实例证明了该模型在一定程度上提高了编制投标价时所用材料价格的准确度。