航空齿轮磨削加工安装偏心误差补偿研究

王鹏，王莹，汪鼎，田莹

(西安航空学院 机械工程学院，西安 710077)

0 引 言

齿轮是现代机械中应用最广泛的传动零件。它具有传动平稳和传动比准确等优点，也是航空发动机中的重要零件。航空发动机中的齿轮制造精度直接影响其传动的性能和安全[1]，因此航空齿轮都属于高精度齿轮。磨齿加工是获得高精度齿轮常用的加工方法，数控成型磨齿机是磨齿加工的重要装备[2]。

关于如何提高成型砂轮磨齿加工的精度，国内外学者进行了很多研究。国外，N.Yoshino等[3]提出了修正砂轮廓形和试算砂轮位置两种齿廓偏差补偿方法，提高齿轮磨削精度；Y.Kobayash等[4]建立了由齿廓偏差求解砂轮安装误差的数学模型来进行砂轮廓形修整，提高磨齿精度；S.R.Park等[5]基于齐次坐标变换提出一种制造机床的综合误差建模方法；A.W.Khan等[6]和Zhao Y等[7]采用变换矩阵、解析二次型、多体系统运动学解决磨齿机制造误差的问题。国内，李平等[8]、宋洪侠等[9]、和张虎等[10]研究了磨齿过程中安装偏心误差与齿廓误差的关系，减小了齿轮齿廓误差；张立功等[11]分析了成形法对磨削斜齿轮的齿形误差的影响；李国龙等[12]针对拓扑修形齿轮的成形磨削误差提出了一种砂轮廓形优化方法；Yu Chunjian等[13-14]针对物理场中耦合条件下的重型数控回转工作台的动静态精度进行了系统研究；石枫[15]论述了合理选择磨齿余量的形式、磨齿余量等因素是提高磨齿质量的基本条件以及蜗杆砂轮对中性对被加工齿轮齿形对称性的影响；梅军炎等[16]通过磨齿方法进而提高磨齿质量。综上所述，针对如何提高磨齿精度国内外的研究主要集中在磨齿余量，工装夹具、降低磨齿机的安装制造误差，提高回转工作台精度，修整砂轮刀具廓形等方面，对于如何在磨齿加工过程中在线减小齿轮误差研究较少。

本文以成型砂轮磨齿机的工作原理为基础，针对直齿圆柱齿轮磨削加工时安装偏心误差对单个齿距偏差和齿距累积总偏差的影响，提出磨齿加工时通过成型砂轮在x、y方向的进给补偿增量来减小齿轮的单个齿距偏差和齿距累积总偏差，以期减小齿轮误差，提高齿轮传动的精度。

1 砂轮成型磨齿加工原理

磨齿加工是提高齿轮精度的常见工艺，磨齿机是磨齿加工的常用设备。目前我国多采用数控成型砂轮磨齿机进行磨齿加工，数控砂轮成型砂轮磨齿机示意图如图1所示。数控转台沿C轴方向的旋转实现工件(齿坯)分度转动；x轴方向实现砂轮架的进给和快退，磨齿加工中砂轮架进给运动称为径向运动；z轴方向实现砂轮在被加工齿轮齿向的往复运动；y轴方向实现砂轮架切向运动，保证砂轮始终用新的面来磨削工件。在磨斜齿轮时，砂轮需要倾斜一个螺旋角，通过滑座沿A轴的旋转来实现。其中z轴和C轴属于磨削运动轴，y轴属于砂轮修整轴，x轴主要用于磨削工件进刀时使用。当进行磨削时，z轴和C轴形成联动关系，砂轮的轴线与齿坯的轴线垂直，砂轮截形的中心线与齿槽截形中心线重合，利用成型的砂轮廓形磨削轮齿的渐开线齿廓。

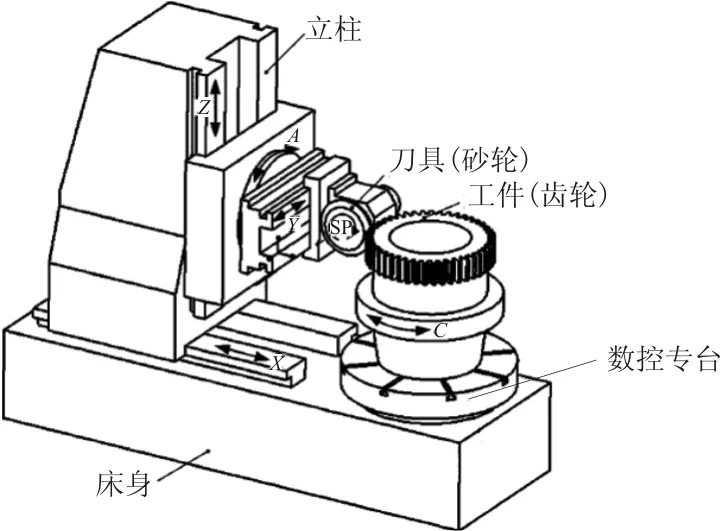
图1 数控砂轮成型磨齿机示意图Fig.1 Schematic diagram of CNC grinding machine for grinding wheel

2 齿坯安装偏心误差对磨齿精度的影响

磨齿精度取决于磨齿机的制造精度、砂轮刀具的廓形精度以及齿坯的安装精度。本文主要研究齿坯的安装精度对磨齿精度的影响。齿轮传动最基本的要求是传动平稳、瞬时传动比准确。在齿轮的各项误差指标中，传动的平稳性和传动比准确性主要由轮齿的单个齿距偏差和齿距累积总偏差决定的。

在齿轮端平面上，以齿坯中心为圆心，圆心到齿高中部的距离为半径存在一个圆称为实际分度圆。实际分度圆截得相邻两轮齿同侧齿面间所对应的弧长称为实际齿距。实际齿距与理论齿距的差值称为单个齿距偏差fpt[17]，它反映了一个齿距角内的分度精度以及轮齿在圆周上分布的均匀性。齿距累积总偏差Fp是指在齿轮同侧齿面任意弧长(k=1至k=z)内的最大齿距累积偏差，它表现为齿距累积偏差曲线的总幅度值，Fp为绝对值[18]，它反映了齿轮旋转一圈的转角误差以及一圈内传动比最大变动量。

综上所述，单个齿距偏差fpt是指两个轮齿间同侧齿面上在分度圆上弧长尺寸的偏差，影响齿轮传动的平稳性。齿距累积总偏差Fp是指单个齿距偏差累积起来产生的总偏差，影响齿轮传动比的准确性。齿距累积总偏差是由每个轮齿的单个齿距偏差共同作用引起的。

磨齿加工时，齿坯安装在回转工作台上，因存在齿坯精度误差，回转工作台制造误差和人为安装误差，导致齿坯的几何中心与数控回转工作台的回转中心存在偏心误差。偏心误差加工模型如图2所示。其齿坯几何中心O1与数控回转台的中心O有安装偏心ej。实线圆为加工节圆，虚线圆为理论节圆。理论节圆上的轮齿应均匀分布，但加工时由于齿坯安装偏心误差的存在，导致轮齿在加工节圆上均匀分布。假设在切削节圆的中心角θ范围内，均匀分布k个轮齿，因理论节圆与加工节圆不重合，轮齿在理论节圆分布不均匀，产生单个齿距偏差和齿距累积总偏差，降低了齿轮精度。

图2 偏心误差加工模型Fig.2 Eccentricity error machining model

以“左齿面”为例，分析理论节圆上的实际位置与其理论位置之间的差距。由图2可知，在理论节圆上，ej值很小，近似由弧长代替，第一个齿实际位置与理论位置相距弧长近似等于ejtgα。因此，第k个齿的实际位置与理论位置相距弧长为

Δt=ejsinθ+ejcosθtgα

(1)

式中：ej为偏心误差；α单位为分(文中α单位与此相同)。

当式(1)等于0时，即Δt=ejsinθ+ejcosθtgα=0，可得tgθ=-tgα。当θ=-α或θ=π-α时，Δt=0，则该轮齿“左齿面”在理论节圆上的实际位置与理论位置是重合的。

(2)

当α=20°时，Δt∑=2.13ej，将Δtmax的ej带入式(1)，可得：

Δt=Δtmax(cosαsinθ+cosθsinα)

=Δtmaxsin(θ+α)

(3)

式(3)表示轮齿“左齿面”的累积偏差，即它们在理论节圆上的实际位置与理论位置之间相距的弧长。

同理，“右齿面”的累积偏差为式(4)。

Δt=Δtmaxsin(θ-α)

(4)

在式(3)和式(4)中，Δtmax=ej/cosα。齿距累积总偏差曲线，如图3所示。其中，图(a)中的y轴Δt表示各齿“左齿面”的齿距累积总偏差，图(b)中的y轴Δt表示“右齿面”的齿距累积总偏差，x轴θ表示相位角。

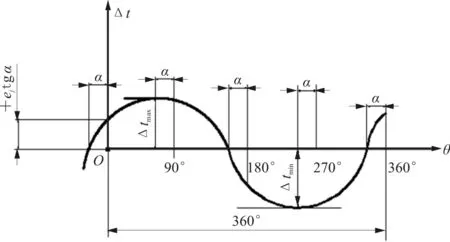
(a) 左齿面

(b) 右齿面图3 齿距累积总偏差曲线Fig.3 Cumulative total deviation curve of pitch

偏心距对于齿距累积总偏差以最大齿距差作为振幅呈三角函数变化，各齿的次序以相位角θ表示，其波峰值和波谷值均为最大和最小的齿距差。安装位置和齿轮参数决定了压力角α和初相位θ[19-20]。

由于单个齿距偏差影响齿轮传动的平稳性，同时影响齿距累积总偏差，而齿距累积总偏差影响齿轮传动比的正确性。由式(2)可知，当压力角α一定时，齿距累积总偏差与安装偏心误差ej成正比关系。因此，当齿坯安装偏心误差增大时，导致磨齿加工时单个齿距偏差和齿距累积总偏差增加，降低了齿轮精度以及传动的平稳性和传动比的准确性。本文提出磨削加工偏心误差补偿法，以期提高齿轮传动精度。

3 磨削加工偏心误差补偿

磨齿加工时，齿坯存在偏心，砂轮刀具相对齿坯孔轴心线的径向距离和切向距离产生变化，因此需要调整砂轮在x轴、y轴方向上的进给量。以机床的固定中O为坐标原点，Ox为径向运动轴(x轴)，Oy为砂轮轴向进给轴(y轴)。偏心磨削加工轮齿分布图，如图4所示。

第一个齿的加工，齿坯是以O1为圆心，砂轮在p1f的位置，砂轮的径向位置与齿坯的几何圆心、机床工作台的旋转中心O在同一条直线上。所以在此位置，砂轮在x轴方向上和y轴方向上的进给增量应分别为：Δx1=e，Δy1=0。然后工作台旋转轴C轴转过一个分度角φ(齿轮在分度过程中逆时针旋转)，开始第二个齿加工，在齿坯安装无偏心的情况下，砂轮进给方向必须要求和工件的直径方向一致，而且总是在x轴上。存在偏心距e的情况下，如果砂轮进给方向仍然保持在x轴方向上不变，磨削加工的轮齿是不准确的，应对砂轮的位置调整，使得砂轮沿切向轴方向，到达p2m的位置，且在x轴方向上和齿坯的圆心O2在同一水平位置。因此，砂轮在x轴方向上和y轴方向上的进给增量为：Δx2=ecosφ，Δy2=esinφ。加工到第三个齿时，砂轮在x轴方向上和y轴方向上的进给增量分别为：Δx3=ecos2φ，Δy3=esin2φ。由此类推，加工第k个齿时，砂轮在x轴方向上和y轴方向上的进给增量为式(5)。

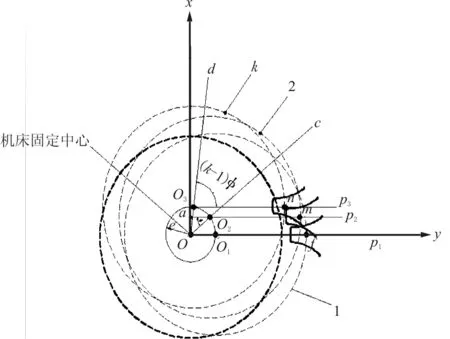
图4 偏心磨齿加工轮齿分布图Fig.4 Gear distribution of eccentric gear grinding

由于几何偏心的方向与磨削加工方向的起始位置之间存在夹角θ，引入矢量e对砂轮磨削起始点的初始相位角θ，得到齿坯安装偏心引起的砂轮在x轴方向上进给增量Δx和y轴方向上进给增量Δy的进给增量的关系表达式(式(6))。

式中：e为偏心量；θ为初始相位角；φ为分度角(360/z)；Δx为x轴的进给增量；Δx为y轴的进给增量。

从式(6)可以看出：砂轮x轴方向进给增量以几何偏心e为振幅呈余弦变化，y轴方向进给增量以几何偏心e为振幅呈正弦变化。通过式(6)可以计算成型砂轮在x轴和y轴方向上进给补偿增量Δx和Δx。

4 磨齿加工偏心误差补偿实验

在YK73125数控成形磨齿机的CAM系统中，嵌入齿坯安装偏心误差补偿模块，用户测量并输入安装偏心误差e，在CAM系统中计算砂轮在x，y两轴方向上进给补偿增量的Δx和Δy，完成偏心误差补偿磨齿加工。

4.1 普通砂轮成型磨齿实验

利用 YK73125数控成型砂轮磨齿机进行磨齿实验，加工齿轮精度可达到5级标准，磨齿机要求安装偏心距小于0.004 mm。待加工标准渐开线，直齿圆柱齿轮主要参数：Z=35，m=16，实际测量安装偏心误差0.003 mm，安装偏心误差满足磨齿机要求，未采用偏心误差补偿进行磨齿加工，对每个轮齿的左右齿面进行测量，测量结果如图5～图6所示。

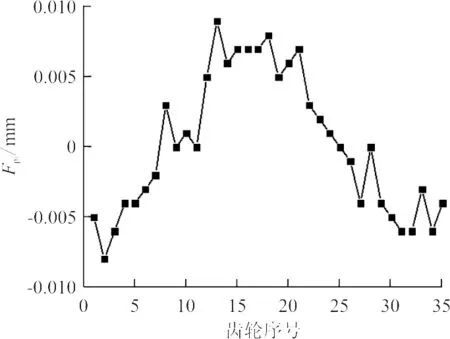
(a) 左齿面

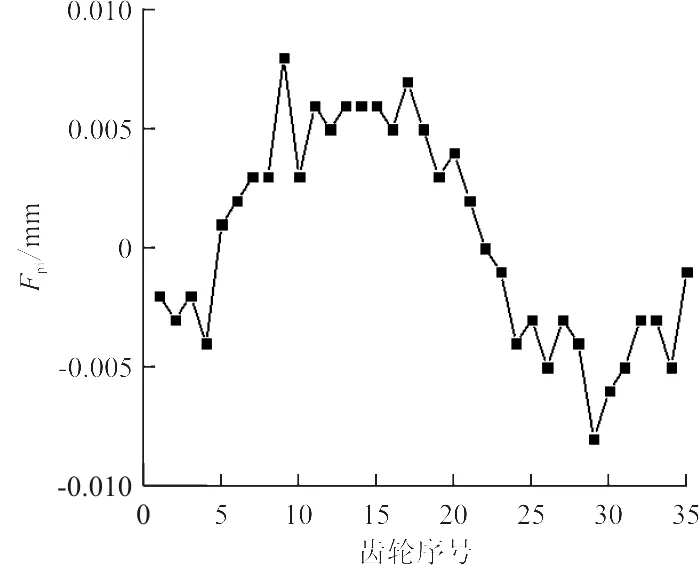
(b) 右齿面图5 单个齿距偏差Fig.5 Single pitch error

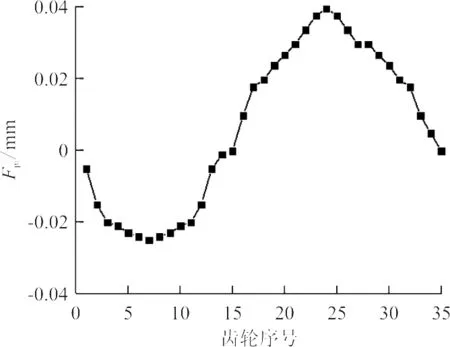
(a) 左齿面

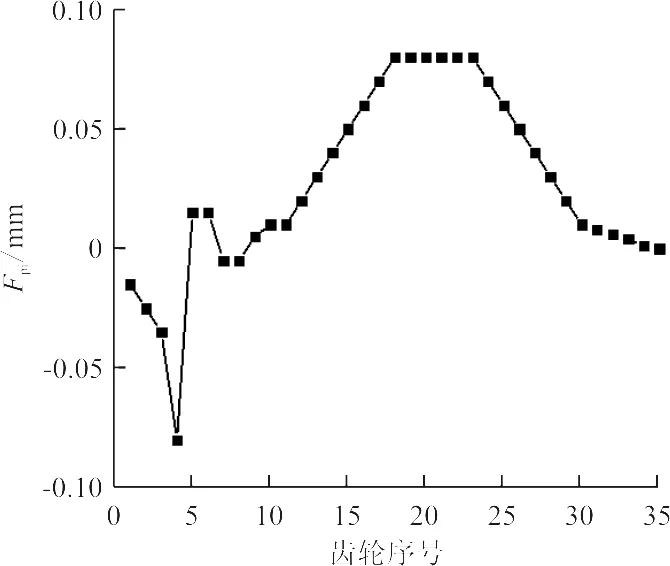
(b) 右齿面图6 齿距累积总偏差Fig.6 Accumulation error of tooth spacing

通过实验数据进行计算，左齿面单个齿距极限偏差fp=8.5 μm，齿距累积总偏差Fp=65.4 μm；右齿单个齿距极限偏差fp=-7.7 μm，齿距累积总偏差Fp=66 μm。

4.2 偏心误差补偿磨齿实验

采用偏心误差补偿加工相同参数的齿轮，为了体现补偿效果，实验采用较大的偏心距。测量安装偏心距e=0.036 mm。根据砂轮进给增量表达式，在CAM系统中进行进给增量补偿计算，得到磨削35个齿的进给补偿增量Δxi、Δyi，如表1所示。通过35个齿的进给补偿增量Δxi、Δyi，采用偏心误差补偿进行磨齿。测量结果如图7～图8所示 。

表1 进给补偿增量表Table 1 Feed compensation increment

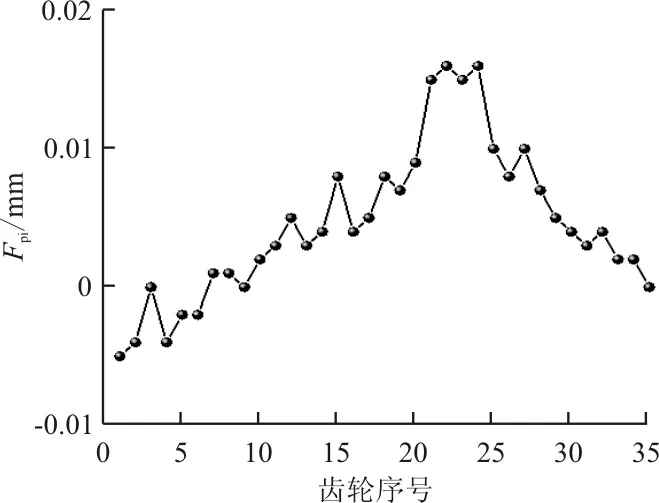
(a) 左齿面

(b) 右齿面图7 单个齿距偏差Fig.7 Single pitch error

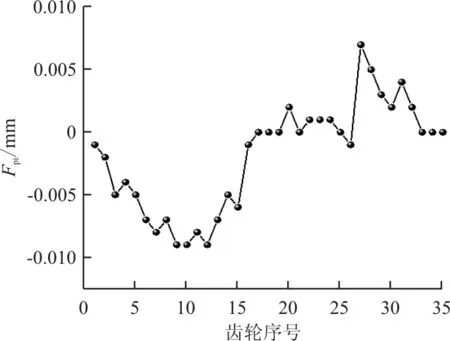
(a) 左齿面

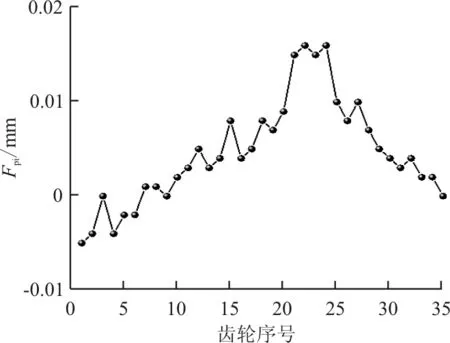
(b) 右齿面图8 齿距累积总偏差Fig.8 Accumulation error of tooth spacing

通过实验数据进行计算，左齿面单个齿距极限偏差fp=7.6 μm，齿距累积总偏差Fp=15.8 μm；右齿单个齿距极限偏差fp=6.1 μm，齿距累积总偏差Fp=22.7 μm。

4.3 实验结果分析

通过对上述左右齿面的齿距累积总偏差(Fp)和单个齿距偏差(fp)的测量曲线分析计算，得到的实验测量数据，如表2所示。

表2 实验测量数据Table 2 Experimental measurement data

从表2可以看出：采用偏心误差补偿加工，左右齿面单个齿距极限偏差和齿距累积总偏差与未采用补偿加工相比较，左右齿面单个齿距极限偏差和齿距累积总偏差的绝对值有了显著减小，表明安装偏心误差对磨齿加工的误差存在显著影响。

同时，从表2可以看出：存在较大偏心误差的情况下，采用偏心误差补偿进行磨齿。齿轮的左齿面单个齿距极限偏差绝对值减小了0.9 μm，齿距累积总偏差减小了49.6 μm；右齿面单个齿距极限偏差绝对值减小了1.6 μm，齿距累积总偏差减小了43.3 μm。采用偏心误差补偿进行磨齿，可以减小单个齿距极限偏差和齿距累积总偏差。

根据ISO1328标准查得：5级精度标准直齿圆柱齿轮，模数m=16，齿数Z=35，分度圆直径D=560 mm，齿距累积总偏差Fp=36.0 μm，单个齿距极限偏差fp=10.0 μm。未补偿的磨齿加工，导致齿轮左右两个齿面齿距累积总偏差Fp，左齿面单个齿距极限偏差fp均未能达到5级精度标准。采用安装偏心误差补偿的方法进行磨齿，所得齿轮的单个齿距极限偏差和齿距累积总偏差均可达到5级精度标准要求。

5 结 论

(1) 本文以数控成型砂轮磨齿机工作原理为基础，建立了安装偏心误差加工几何模型，当齿轮压力角α一定时，单个齿距误差和齿距累积总偏差与安装偏心误差ej成正比关系。当齿坯安装偏心误差增大时，导致磨齿加工时单个齿距偏差和齿距累积总偏差增加，降低齿轮精度。

(2) 本文提出了基于磨齿加工的安装偏心误差补偿法，建立了磨齿加工偏心误差补偿数学模型，通过计算得出磨齿加工时成型砂轮径向和切向的进给补偿增量。磨齿加工时，调整砂轮的进给补偿增量，可减小被加工齿轮的单个齿距偏差和齿距累积总偏差。

(3) 通过YK73125数控成型砂轮磨齿机进行偏心误差补偿实验，齿轮的左右齿面单个齿距极限偏差绝对值分别减小了0.9 μm和1.6 μm，齿距累积总偏差绝对值分别减小了49.6 μm和43.3 μm。采用偏心误差补偿法进行磨齿加工减小了安装偏心误差对齿轮精度的影响，提高了齿轮精度，从而为高精度航空齿轮的磨削加工提供了可靠的理论支持。