线型无线传感器网络中一种联合优化中继节点选择策略*

罗海波,阮志强

(1.闽江学院计算机科学系,福州 350121;2.福建省信息处理与智能控制重点实验室,福州 350121;3.数字福建智能化生产物联网实验室,福州 350121;4.闽江学院工业机器人应用福建省高校工程研究中心,福州 350121)

在无线传感器网络WSNs(Wireless Sensor Networks)中,部署了大量由电池供电的节点,因此节约能耗是设计无线传感器网络媒质访问控制MAC(Medium Access Control)及路由算法的主要挑战之一[1-3]。线型无线传感器网络是一种拓扑结构呈现一定线型性的特殊网络结构,如图1所示,该类型网络可广泛应用于道路、桥梁、隧道、过道、管道、河流等监控领域,在这种类型的WSNs中,节点往往等距离静态部署,具有大量的中继节点和中继跳数,因此网络时延将比其他类型的WSNs大[4-5],另一方面,网络拓扑的线型性也导致网络连接更加脆弱,部分连续相邻节点耗尽能量后将导致整个网络链路的中断。因此,在线型WSNs中,设计一个能耗均衡与时延优化的中继节点选择算法尤为关键。

最远传输距离算法(MFR)[6]总是选择通信范围内最远处的节点作为中继节点,以期达到最低功耗及最少时延,但是MFR算法将导致部分节点过早死亡。Ramaiyan等人[7]从理论上分析了最优功率控制及最佳转发距离,并提出应在发射功率与传输距离之间找到一个平衡点,从而得到最优中继距离和最低网络能耗。

Luo J等人[8]则受到随机路由策略[9-10]的启发,针对线型无线传感器网络提出了一种基于随机路由的中继节点选择算法ENS_OR,该算法基于节点剩余能量,设计了一个最优化节点选择函数,从而可以为前向转发集中的每个节点计算中继转发优先级,优先级较高的节点将优先获得转发权。但在ENS_OR算法中,优先权的获取是通过设定定时器得到的,而定时器的设定,跟节点的剩余能量直接相关,这就将导致随着网络的运行,由于节点剩余能量下降,即使具有较高优先级的节点,也需要等待更长的时间才进行数据的中继。GeRaF[11]则是一个经典的基于地理位置的随机路由中继节点选择策略,在该算法中,每个数据包均携带了发送节点和目标节点的位置信息,离目标节点更近的节点将获得优先转发权。上述算法均未考虑到线型无线传感器网络的时延问题,为了均衡优化能耗与时延,TE-OR算法[12]提出了一种自适应的中继节点选择算法,TE-OR将数据包按时间敏感性分类,并假定节点的发射功率不变,利用协调因子来适应数据包的类型,但由于设定了节点的发射功率是固定的,因此未考虑到能耗最优传输距离。

本文基于随机路由的基本思想,并考虑到随机路由的广播属性,首先推算出全局能耗最优的传输距离,而后考虑到紧急数据包的时延要求,通过调节发射功率,分别在最远传输距离及能耗最优距离范围内为紧急数据包和普通数据包选择最佳中继节点,从而实现时延-能耗的平衡最优化。

图1 线型无线传感器网络应用背景及抽象拓扑模型

1 能耗最优传输距离

线型无线传感器网络的拓扑模型如图1所示,假定节点等距均匀分布,并连续编号。两个相邻节点之间的距离为DN,节点的通信范围为R=nDN,节点发送一个k-bit数据包的能耗为ETx(k,d)=(ETelec+Eampdτ),接收k-bit数据包的能耗为ERx(k)=EReleck,其中,ETelec与ERelec为节点发送和接收电路的基础能耗,Eamp为发送功放电路的能耗系数[13],τ为无线环境的信道衰减因子,一般满足:2≤τ≤4.

假设在线型传感器网络中,每个节点的发射距离均为R(R=nDN),当节点Ni发送kbit数据到Sink节点Ns时,每个中继节点发送能耗为ETx(k,R)。数据在中继过程中,每一跳中继时,R范围内的所有节点(共2n个)均可侦听到该数据包,每个节点的侦听功耗为ERx(k),则每跳中继造成的侦听总能耗为2n×ERx(k)。可见,此时网络总能耗为:

(1)

为了求得总能耗的极值,可将式(1)对R求一阶导数,可得:

(2)

(3)

Rop={ETelec/[(τ-1)Eamp]}1/τ

(4)

2 功率可调的能耗-时延联合优化算法

在能耗最小化的同时,还需要考虑数据包时延,特别是对于紧急数据的传输,时延是非常敏感的性能指标,在线型无线传感器网络中,由于传输跳数较多,数据的时延主要产生在中继环节,因此应尽可能减少紧急数据的传递跳数,即每一跳应尽可能传递地远,此时要求每一跳都选择通信范围内最远的节点作为下一跳中继节点,直至最远处节点的能源被耗尽,再选择次远处节点,依此类推。在线型无线传感器网络中,节点近似等距离部署,节点的ID号(编号)可与其地理位置关联起来,假设选择的中继节点为Nc,则此时要求c的值应该尽可能的大。

但另一方面,在无线传感器网络中,我们还应考虑节点能量消耗的均衡性与公平性,部分节点的过早死亡将在线型无线传感器网络中形成“盲区”,由于线型无线传感器网络特殊的拓扑结构,这些“盲区”甚至可能使得网络连接中断。为实现能耗的均衡性,可构建一个方差函数来优化中继节点的选择,使得节点在选定下一跳中继节点后,其通信范围内(R=nDN)的所有节点的剩余能量方差最小[12]。具体的说,节点Ni选定Nc(i+1≤c≤i+n)作为下一跳中继节点,在节点Nc完成这个k-bit数据包中继后,Ni的前向节点集CNi={Nj|i+1≤j≤i+n,j∈Z}的剩余能量方差可表示为:

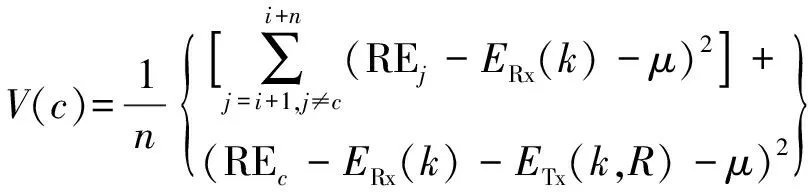
(5)

式中:REj表示节点Nj的剩余能量,μ为节点Nc完成数据发送后,前向节点集CNi的剩余能量均值。总体上看,不管选择哪个前向节点作为下一跳中继节点,集合CNi都将消耗nERx(k)的接收能耗及ETx(k,R)发送能耗,因此剩余能量均值μ是一个与c无关的值。为了实现能耗的均衡化,V(c)应该取最小值。另一方面,根据上述的分析,为了使得数据包时延尽可能的小,c的值应该尽可能的大。则构建联合优化目标函数如下:

F(c)=V(c)-γc

(6)

式中,γ为调节能耗与时延的协调因子,且γ越大,越有利于降低数据包时延,反之则有利于提高能耗均衡性。显然地,我们应该选择最优化中继节点Nc,使得F(c)的值最小,即:

mini+1≤c≤i+nF(c)=mini+1≤c≤i+n[V(c)-γc]

(7)

将式(5)代入式(7),并消除与变量c无关的项,经过恒等转换,式(7)可等价为式(8):

maxi+1≤c≤i+n{[2ETx(k,R)×REc]/n+γc}

(8)

从式(8)可以看出,根据应用需求设定好协调因子γ之后,我们可以根据节点的剩余能量REc及地理位置(即编号c)来求得最优的中继节点。当节点Ni有数据需要发送时,根据式(8)得到前向节点集中所有节点的计算结果,并根据结果大小进行优先级排序,结果较大的节点,优先级越高。并将该优先级顺序信息插入到数据包中。CNi中的节点接收到数据包后,直接提取优先级顺序启动不同的定时器,优先级高的,定时时间将最短,在定时时间到达后,回复ACK数据包给源节点Ni,并进行数据包的转发。其他节点在侦听到ACK消息后,则立刻停止定时器并放弃该数据包的转发。

总结来看,根据上述第1节的分析,为了降低网络总体能耗,要求每跳中继的最优传输距离为Rop。但从时延性能的角度出发,则要求每跳要尽可能地远,以便减少传输跳数,此时最佳传输距离为Rmax=mDN。因此,为了满足时延、耗能最少及均衡性3个方面的需求,本文针对数据的时延要求属性,提出了一个随机路由中能耗-时延自适应优化中继节点选择算法LEARS(Latency-Energy Adaptable Relay-node Selection algorithm),对于紧急数据包,节点调整最大发射能量为ETx(k,Rmax),此时可在最大传输距离Rmax范围内根据式(8)选择最优中继节点;而对于普通数据包,则降低发射能量到ETx(k,Rop),并在Rop范围内根据式(8)选择最优中继节点。这样,则可达到能耗与时延的自适应均衡优化。算法的伪代码描述如下:

算法1功率可调的时延-能耗自适应优化中继节点选择算法(LEARS)

在上述算法中,TACK为ACK消息的发送时间,TSIFS为无线通信中必须具备的短帧间时延,用于在 2个连续的消息中插入时间空隙,以便接收端及时进行数据的接收处理。从该算法可看出,timer(j)只与节点的优先序PO(j)相关,而与前向集节点的剩余能量分布无关,当网络中节点的剩余能量降低时,优先级相同的节点在不同时刻具有恒定的timer时延,这对于提高时间敏感消息的实时性尤为重要。

3 仿真分析

为验证我们所提出的LEARS算法,本文使用MATLAB对其进行仿真分析,并与GeRaF、MTE(R=5 m)及TE-OR算法进行比较。与本文基于前向地理位置转发思想类似,GeRaF也是一个基于地理位置的随机中继节点选择策略,而MTE则是一种逐跳最小能量转发策略,它们都旨在最小化网络能耗。TE-OR算法则是一种专门针对线型拓扑网络能耗-时延联合优化算法。

考察了节点平均剩余能量、节点剩余能量方差、平均包时延、死亡节点个数、网络生命周期等5个性能指标。仿真参数的设置与TE-OR保持一致,由 1个源节点以1 s为周期产生数据包,并发送到Sink节点,并按50%的概率随机生成紧急数据包和普通数据包。源节点与Sink节点间线性等距部署500个节点,节点之间相距5 m,TE-OR中的发送距离与LEARS算法中的Rmax均设置为50 m,即假定TE-OR将发射功率固定设置为最大值。ETelec、ERelec、Eamp分别为50×10-9J/bit、25×10-9J/bit、18×10-11J/(bit·m2),信道衰减因子τ=2,则Rop=(50×(10-9/18)×10-11)1/2≈16.7 m,本文在实验时,设Rop=20 m。其他参数设置如表1所示。可计算得到接收数据能耗ERx(800)=2×10-5J。由于本文主要通过控制发射功率来调整通信距离,从而适应不同的数据包类型,因此紧急数据包和普通数据包的协调因子γ均设定为1α(α=2ETx(k,R)/n)。所有节点的初始能量为1 J,当能量消耗到只剩下0.2 J时,认定节点死亡。

表1 仿真参数

图2所示为4种算法的平均剩余能量变化情况。随着网络的运行,4个算法的平均剩余能量均将下降至接近0.2 J,但MTE的平均剩余能量下限值是最大的,为0.226 J,这是由于MTE采用每跳最短中继法,因此只要存在一个节点能量下降到0.2 J,数据包即无法继续传递,即使后续节点仍然具有一定的剩余能量。此外,MTE的平均剩余能量下降最快,而LEARS下降得最慢。因为LEARS在传递普通数据包时,每跳距离尽可能接近最优能耗传输距离Rop,因此,相比TE-OR单纯使用协调因子γ来调节普通数据包在Rmax范围内选定中继节点,具有更佳的能耗表现。

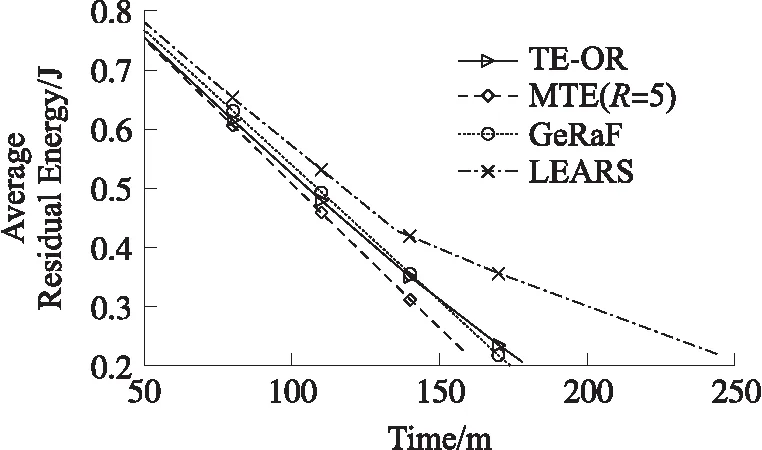
图2 平均剩余能量

网络的剩余能量的方差变化情况如图3所示,总体上看,TE-OR、GeRaF、LEARS的剩余能量方差均呈现出先变大再变小的趋势,且具有阶梯振荡式特性,这是因为随着数据的传递,部分节点将优先消耗能量,造成方差总体上升,随后根据算法各自的策略,其他节点也将被选定为中继节点,因此方差又会短时降低,随后又将升高。GeRaF剩余能量方差的上升和下降是最快的,相比之下,TE-OR与LEARS则平缓得多,MTE总是每跳中继,所有节点均等消耗能量,因此方差总是0。此外,我们可以从图中看出,由于LEARS动态调节功率来转发不同类型的消息,LEARS的方差将比TE-OR要大。

图3 剩余能量方差

图4 时延

图4为数据包的平均时延,本文统计所有被Sink节点成功接收的数据包的平均端到端时延,MTE的平均时延总是维持在约1.8 s,远大于其他算法,因此本文没有将它画在图4中。为了区分TE-OR及LEARS中不同数据包类型的时延性能,图4中分别画出了它们的紧急数据和普通数据包的平均时延。可以看出,LEARS紧急数据包时延与TE-OR的相当,约为179 ms,且比GeRaF低18 ms,但LEARS普通数据包时延则明显高出不少,这是由于LEARS的普通数据包在中继时,最远传输距离为Rop=20 m,远小于紧急数据包的Rmax=50 m,因此普通数据包将具有更多的中继跳数,从而导致了更高的数据包时延。

图5和图6分别为节点死亡个数及网络生命周期的对比图。总体上看,MTE在网络运行到157 min时,产生第1个死亡节点,因此网络也在此时中断。其他3个算法,死亡节点个数均阶梯式上升,但LEARS的死亡节点个数在大部分时间段分别低于TE-OR及GeRaF约20个及110个。此外,LEARS具有最长的网络生命周期,比TE-OR延长了约65 min。

图5 死亡节点个数

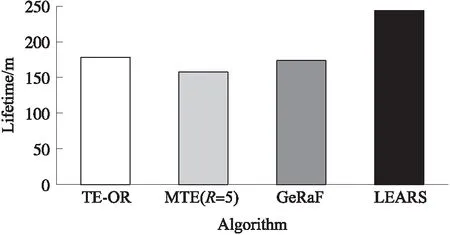
图6 网络生命周期

4 结论

针对线型无线传感器网络中存在的时延-能耗均衡优化问题,本文提出了一种自适应优化算法,针对数据的时间敏感性,选择不同的发射功率和中继距离,并在通信范围内选出联合最优的中继节点。仿真结果表明,本文所提出的LEARS算法可与TE-OR算法一样,优先保证紧急数据的实时传输,并可进一步降低了网络总体能耗,大幅度延长了网络的生命周期。接下来,我们将搭建物理测验平台对该算法进行评估及进行进一步的优化。