WSNs中数据融合树的时隙分配算法*
臧景才,王自力,郑 鑫
(1.青海广播电视大学继续教育学院,青海 西宁 810000;2.驻马店职业技术学院信息工程系,河南 驻马店 463000;3.黄淮学院信息工程学院,河南 驻马店 463000)
无线传感网络WSNs(Wireless Sensor Networks)由大量的微型传感节点组成[1-2],这些传感节点具有感测、通信能力,进而实现对环境的监测目的。目前,WSNs已广泛应用于军事勘测、环境管理以及健康医疗等领域。在多数的应用中,数据融合是最基本的技术。通过数据融合,将从多个传感节点所接收数据进行汇集,再经处理后传输信宿。在数据融合过程中,中间节点将所收集的数据与自己的数据进行融合成一个数据包,然后再转发。目前,融合技术有合并、最大求和,平均等策略[3-4]。
最小化数据融合时延是融合技术最重要性能指标。所谓融合时延是指数据融合数据传输至信宿的时间[5-6]。最小化数据融合时延就是最小时延的融合策略问题MLAS(Minimum-Latency Aggregation Scheduling)。MLAS问题就是最快找到无碰撞的数据融合时隙[7]。实际上,节点间的干扰是影响数据融合的主要因素。当节点在同一时刻监听两个或两个以上的信号时,就发生了信号干扰。一旦产生了干扰,节点就无法成功再接收任何数据,这就使得发射节点需要重新传输数据。
文献[8-9]通过分析证实,由于重传数据消耗了大量的能量,碰撞是WSNs的挑战之一。此外,在MAC层(硬件)解决碰撞问题比在应用层(时隙分配策略)增加了大量的传输时延[10-12]。例如,文献[11]提出二次独立集的数据融合算法,该算法引用时分复用概念,并二次构建最大独立集,进而降低整合时延。因此,研究人员通过合理分配融合时隙可解决MLAS问题,进而减少传输时延,并降低碰撞概率。
此外,最小化能耗也是WSNs的研究热点。近期,周期工作DC(Duty Cycling)[13-14]技术得到广泛关注。在DC中,每个节点只工作一小段时间,而其余的时间进行休眠。DC技术能够有效节省能量,降低能耗。然而,如何控制休眠时间是DC的关键,并且DC技术也增加了数据传输时延。
为此,针对基于DC技术的WSNs,研究如何解决MLAS问题,并提出免碰撞的数据融合树的时隙分配算法CF-DGSS(Collision-Free Data Aggregation Slots Scheduling Algorithm for Duty-Cycled Wireless Sensor Networks)。CF-DGSS算法以融合树为基础,给每个节点分配融合数据时隙,并保证无碰撞,进而最小化融合时延。仿真数据表明,提出的CF-DGSS算法能够有效降低传输时延。因此,本文的主要工作可归纳以下3点:①为了减少碰撞,定义碰撞集;②通过节点秩定义数据融合树,并据此分配时隙,进而降低时延;③构建仿真平台,通过数据分析了算法性能。

图1 基于DC的WSNs的工作时隙
1 网络模型
建立图论G=(V,E)的无线传感网络,其中V为传感节点集,E为边集。同时假定传感节点的传输距离为R。如果两个节点i、j间的欧式距离‖i-j‖小于R,则它们间存在一条边(i,j)∈E。
在DC的无线传感网络,将每个节点的整个寿命划分多个工作时期,且每个时期时长相同。每个时期又划分为T个工作时隙。每个节点i随机在从T个时隙中选择一个时隙用于传输数据包或接收数据包。假定节点i所选择的工作时隙表示为A(i),且这个时隙称为节点i的活动时隙,而其他T-1个时隙为休眠时隙,如图1所示。T=5,节点i选择的时隙为2。
假定每个节点仅有一个数据包要传,且每个节点在它的活动时隙只能接收数据包,但是,它能够在任何时隙发送数据。此外,假定节点能够融合它的子节点的数据,并通过数据融合树向它的父节点传输。所谓数据融合就是指将两个或多个数据转换成一个数据包。
此外,一个信宿节点s∈V能够接收其他所有节点的数据,直到网络内所有数据传输至信宿后,数据融合过程才结束。
2 干扰模型
假定节点不能同时接收数据和发送时隙。令R和R′分别表示节点的传输距离和干扰距离,且令R=R′。对于任意节点(假定是节点i),如果满足下列条件,则认为节点i能够成功将数据发送至它的父节点p(i)。
‖i-p(i)‖≤R
(1)
∃x,‖x-p(i)‖≤R,andA[p(x)]=A[p(i)]
(2)
为了解决碰撞问题,保证融合时隙安排策略的无碰撞,给每个传感节点定义碰撞集CS(Conflicting Set)。且每个传感节点在数据融合过程需保存CS。在安排时,传感节点应当保证被分配的传输时隙与CS中其他节点的传输时隙不产生冲突。
为此,接下来,对CS进行定义。节点i的碰撞集为CS(i),其由三部分组成:
①节点i的父节点p(i)的所有子节点,且除节点i外;
②节点i的邻居节点的所有子节点(假定为节点υ)。如果A(υ)=A[p(i)],则节点υ为节点i的CS节点;
③假定p(i)的邻居节点表示为x。如果A[p(x)]=A[p(i)],则节点x称为节点i的CS节点。
如图2所示,12个节点构成了一个数据融合树。以节点8为例,它的CS节点分别为节点υ7、υ9、υ4。即CS(υ8)={υ7,υ9,υ4},其中υ7、υ9、υ4分别满足①、②、③3种情况。
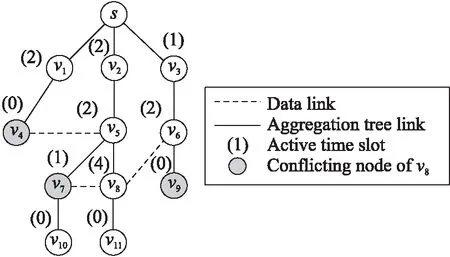
图2 CS集示例
3 CF-DGSS数据融合时隙安排算法
CF-DGSS算法就是依据数据融合树DAT(Data Aggregation Tree),给每个节点分配一个传输或接收数据的时隙,同时保证与其他节点不发生冲突。为此,CF-DGSS算法中的每个节点应当存取以下局部信息。
①节点的秩
假定节点i的秩为rank(i)。rank(i)包含了两项信息,分别为level(i)和节点的ID(i),其中level(i)表示在DAT中节点i离信宿的跳数。如果level(i)>level(j),则rank(i)>rank(j);如果level(i)=level(j),ID(i)>ID(j),则rank(i)>rank(j)。节点可以通过来自信宿s的广播消息,获取这些信息。
②融合时隙
假定tsch(i)表示给节点i分配的工作融合时隙。换而言之,节点i在tsch(i)时隙向它的父节点p(i)传输数据。
③最小的工作时隙tmin(i)
节点i的最小工作时隙就是节点i的子节点中的最大工作时隙。此外,tsch(i)≥tmin(i),∀i∈{Vs}。
④节点i的未安排时隙的子节点数,且表示为nuch(i)。
⑤节点的CS集,即CS(i)。
最后一个就是节点i的禁止工作时隙的集,且表示为FS(i)。换而言之,FS(i)表示节点i不应该分配的工作时隙,进而避免碰撞。
CF-DGSS算法核心思想如下:当节点的后裔节点全部被分配了时隙,而该节点自己本身没有安排时隙,此节点称为未安排节点UE(Unscheduled Node),而已安排的节点称为安排节点RE(Ready Node)。CF-DGSS算法就是优先给秩值高的节点分配时隙。为了防止碰撞,给节点分配的时隙保持相互干扰。一旦分配了时隙,节点就向邻居节点广播通知消息。一旦接收了该消息,邻居节点就更新自己局部变量。
图3描述了CF-DGSS算法分配时隙的过程。首先,网络内每个节点先初始化局部变量。假定RN节点u的秩最大,因此首先给节点u分配工作时隙。如果u是DAT的一个子节点,给它分配的工作时隙tsch(u)设置为1,如Step 4所示。否则的话,节点u的所有子节点已经完成了时隙分配过程。在这种情况下,就依据节点u、p(u)的活动时隙和tmin(u)给节点u分配时隙。

图3 融合时隙分配算法的伪代码
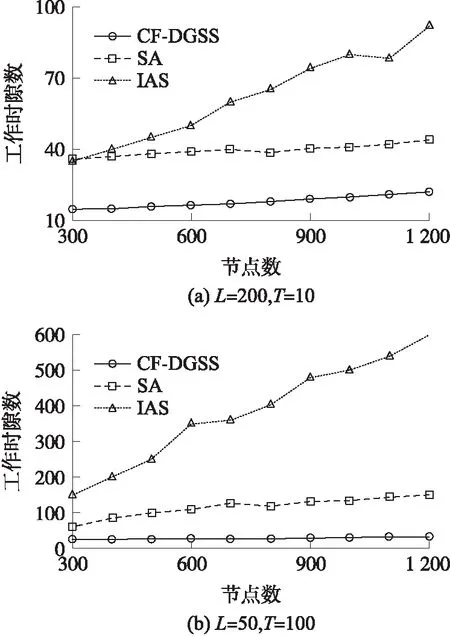
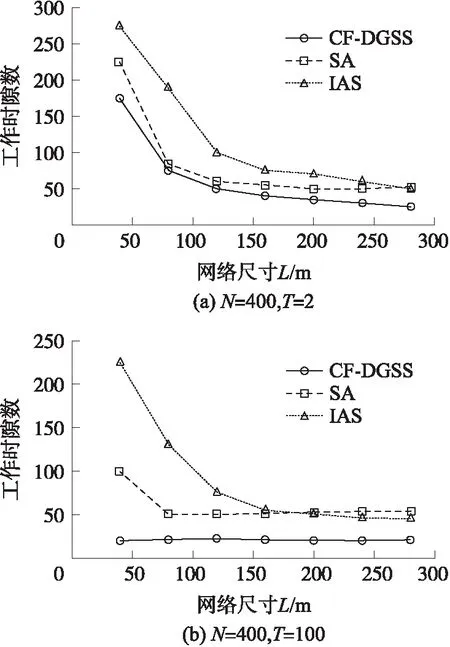
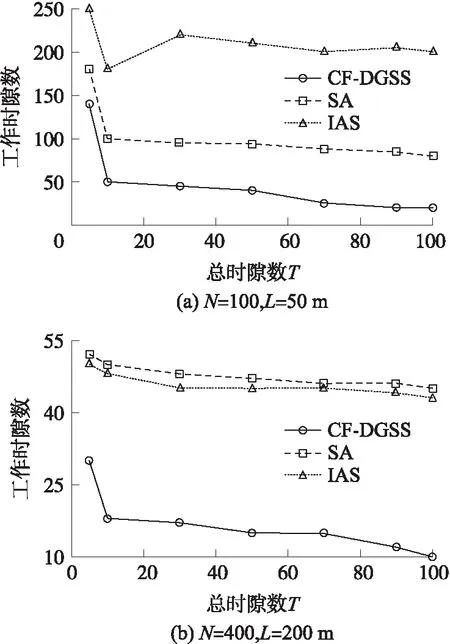
如果A(u) 一旦完成时隙安排,节点u就向它的两跳邻居节点传输MARK消息,其包含节点的ID和它的tsch(u)。如果与节点u冲突的一个UN接收了消息,它就从CS中将节点u移除,同时将tsch(u)加入至FS集,因为节点u已经安排了时隙,如Step 17至 Step 19行。 当接收到来自节点u的消息,如果tsch(u)大于当前tmin[p(u)],p(u)就将nuch(u)减一,并更新它的最小工作时隙tmin[p(u)],如Step 20行至Step 24行所示。最后,当所有节点分配了时隙后,它们就依据这些时隙传输数据。 图4描述了CF-DGSS算法的示例。图4(a)表示了7个节点的活动时隙。而图4(b)为CF-DGSS算法给每个节点分配的数据融合时隙。首先,因为节点υ5位于DCT的叶节点,所以tsch(υ5)=1。将节点υ5的工作时隙与FS(υ5)内的冲突节点的工作时隙进行核对。由于FS(υ5)={tsch(υ4)}={2},节点υ5被安排在时隙1向节点υ2传输数据。 此外,如果A(u) 图4 CF-DGSS算法的时隙安排示例 利用MATLAB软件建立仿真平台,并分析CF-DGSS算法的性能。假定N个传感节点分布于L×L的正方形区域,传感节点传输距离R=30 m。在每个周期内,传感节点从[0,T-1]内选择一个时隙作为工作时隙。 为了更好地比较CF-DGSS算法的性能,选择文献[15]的融合时隙分配算法IAS和文献[16]的SA。主要考查算法的数据融合时延。数据融合时延是指在一个周期内信宿s接收到所有节点数据的时间,在仿真过程中,选用工作时隙数表征数据融合时延,工作时隙数越多,数据融合时延越高,反之,亦然。 考查3个实验场景:①改变节点数N;②改变网络尺寸L;③改变总时隙数T。每次实验,独立重复50次,取平均值作为最终的仿真数据。 4.2.1 改变节点数 在本次实验中,假定节点数N从300至1 200变化,且考虑L=200,T=10和L=50,T=100两种情况。实验数据如图5所示。 从图5可知,提出的CF-DGSS算法具有低的工作时隙。以图5(a)为例,CF-DGSS算法的工作时隙比SA算法降低了55.21%。随着网络尺寸的下降,CF-DGSS算法的优势减弱,在图5(b)中,CF-DGSS算法的工作时隙比SA算法降低了44.50%。CF-DGSS 算法能够获取低的工作时隙数的原因在于:CF-DGSS算法允许多个节点在同一个时隙传输,这减少了所需的时隙数。 图5 工作时隙数 图6 工作时隙数 4.2.2 改变网络尺寸L 在次实验中,假定网络尺寸L从30至300变化,且考虑N=400,T=2和N=400,T=100两种情况。实验数据如图6所示。 对比图6(a)和图6(b)可知,T的增加极大地提高了CF-DGSS算法的性能。此外,随着网络尺寸L的增加,3个算法的工作时隙随之下降。但是,当L大于100后,工作时隙数不再随L变化,而是趋于平稳。 从图6可知,提出的CF-DGSS算法的工作时隙数比IAS和SA,分别平均下降了约65.04%和50.95%。 4.2.3 改变总时隙数T 在本次实验中,假定节点数T从5至100变化,且考虑N=400,L=50 m和N=400,L=200 m两种情况。实验数据如图7所示。 从图7(a)可知,当L=50 m时,CF-DGSS算法比SA算法的工作时隙数平均下降了约14.23%。此外,T值越大,CF-DGSS算法的时隙性能越好。相反,从图7(b)可知,当L=200 m时,CF-DGSS算法的工作时隙数下降。 图7 工作时隙数 针对无线传感网络的数据融合问题,提出免碰撞的数据融合树的时隙分配算法CF-DGSS。CF-DGSS算法旨在降低融合时延,并减少节点间的相互干扰。CF-DGSS算法先依据DAT树,计算节点秩,然后给每个节点分配融合时隙,并通过冲突集CS的设定,降低节点间的干扰。实验数据表明,与SA和IAS算法相比,提出的CF-DGSS算法能够有效地降低融合时延。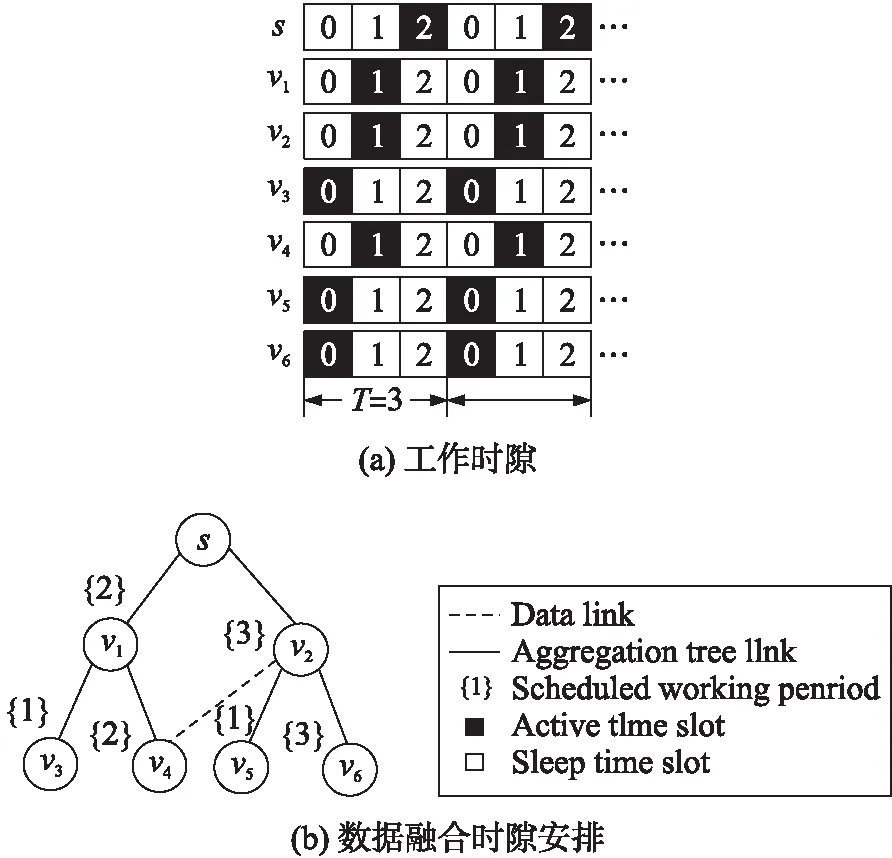
4 性能分析
4.1 仿真参数
4.2 数据分析
5 总结

