空空导弹两阶段性能退化部件可靠性建模

杨立安，张国豪，朱仲波

（1.中国人民解放军空军勤务学院航空弹药保障系，江苏 徐州221000；2.中国人民解放军94303部队，山东 潍坊261000；3.中国人民解放军94995部队，江苏 如皋226500）

0 引言

空空导弹被誉为“空战之剑”，是由歼击机、强击机、直升机、轰炸机等携带发射，攻击空中目标的导弹，对夺取制空权、保持空中优势至关重要。空空导弹在长时间的贮存中通常会出现质量问题或技术性能下降现象，进而导致故障的发生，因此，需要对空空导弹贮存可靠性进行合理的分析，建立适当的数学模型，得出详细的研究结果。导弹的故障通常是由其内在失效机理与外部环境因素综合作用导致的，这是一个复杂的过程，但是从故障的发展进程来看，导弹的故障可分为突发故障与退化故障两种。退化故障[1]表现为导弹的性能状态随存储时间的延长而逐渐下降，监测参数的测试数据逐渐偏离标准值并最终超出规定阈值。本文通过建立两阶段退化过程模型，确定了阶段退化过程可靠度函数，对空空导弹部件进行了贮存可靠性分析，解决空空导弹部件可靠性预测问题。

1 逆高斯过程和维纳过程

1968年Wasan首次发表逆高斯过程[2]，但由于当时无法在实践工程中得到检验，因此逆高斯过程并没有被重视。直到2010年，逆高斯过程才再次进入学者视线，在实践中得到认证。2012年，学者Ye和Chen给出了逆高斯过程物理背景的正式解释，提出逆高斯过程是解决产品单调退化过程问题最合适的模型。

在逆高斯过程中，性能退化量{X（t）；t＞ 0}具有下列性质[3]：

（1）X（0）＝ 0依概率1恒成立；

（2）对于任意 t＞ s ＞ u，X（t）-X（s）≥ 0，X（s）-X（u）≥ 0，X（t）-X（s）和 X（s））-X（u）相互独立；

（3）对于任意 t ＞ s ≥ 0，X（t）-X（s）～IG[Λ（t）- Λ（s），λ（Λ（t）- Λ（s））2]

式中：λ是逆高斯过程的刻度参数；Λ（t）是单调增函数，Λ（0）＝ 0；IG[Λ（t）- Λ（s），λ（Λ（t）- Λ（s））2]是逆高斯过程的分布函数。

维纳过程[4]是一个重要的独立增量过程，在纯数学中，维纳过程导致了对连续鞅理论[5]的研究，是刻画一系列重要的复杂过程的基本工具。在维纳过程中，性能退化量{X（t）；t＞ 0}具有下列性质：

（1）X（0）＝ 0依概率1恒成立；

（2）对于任意 t ＞ s ＞ u，X（t）-X（s）≥ 0，X（s）-X（u）≥ 0，X（t）-X（s）和 X（s））-X（u）相互独立，服从正态分布；

（3）对于任意时刻 t＞ 0，X（t）～N（μt，σ2t）

2 两阶段退化过程建模

部件两阶段性能退化指的是贮存过程中性能退化率在某一时刻发生改变，部件性能退化在变点前后分属于两个不同的过程。即初始阶段部件的退化过程服从X1（t；μ1；λ1）；当到达变点τ时，部件的退化过程变为服从X2（t；μ2；λ2）。因此，建立两阶段性能退化模型：

其中，x01，x02分别为两个阶段的初始量；μ1，μ2分别为两个阶段的漂移系数；λ1，λ2分别为两个阶段的扩散系数。

在模型（1）中，若变点τ＝0或τ＝∞，那么两阶段性能退化模型将变成具有单一退化过程的性能退化模型，这里不再过多讨论；由于部件性能退化属于连续过程，即使出现性能退化率的改变但在变点处性能退化量仍然连续[6]，即

3 两阶段退化过程可靠度函数确定

为了对贮存过程中符合两阶段性能退化过程的部件进行有效的分析，根据建立的两阶段性能退化模型确定其可靠度函数。由性能退化理论可知，当部件的性能退化量随时间推移累积达到设定的失效阀值D时，部件首次发生失效，此时对应的贮存时间就是部件的贮存可靠寿命，定义为[7]：

此时，部件的可靠度函数为：

两阶段退化过程在变点前后其退化率不同，服从相异的退化过程，因此确定其可靠度函数时需要分变点前后两种情形分别进行处理。

（1）当0＜t＜τ时，部件服从第一阶段的退化过程[8]，其性能退化服从过程X1（t；x01，μ1，λ1），为了体现一般情况，假设部件的失效概率密度函数为f1（t；x01，μ1，λ1），根据可靠性定理得出t时刻部件的失效分布函数和可靠度函数为：

（2）当τ＜t时，部件服从第二阶段的退化过程[9]，其性能退化服从过程X2（t-τ；x02，μ2，λ2），为了体现一般情况，假设部件的失效概率密度函数为f2（t；x02，μ2，λ2），根据可靠性定理得出 t时刻部件的失效分布函数和可靠度函数为：

因此，将两种情况联立可得两阶段退化过程可靠度函数为：

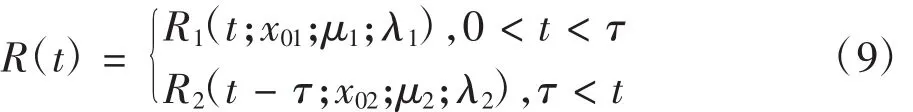
若部件的退化过程服从逆高斯过程，则其可靠度函数为：

若部件的退化过程服从维纳过程，则其可靠度函数为：

选取贮存过程中n个部件测试信息，设X（tij）为第i个部件在tiji=1，2，…，m时的测量值，第i个部共测试mi+1次，其变点为τi且tki≤ τi≤ tki+1.△Xij=Xij-Xij-1为区间△tij=tij-tij-1上性能退化量的变化量。以逆高斯过程为例：

⑴当0＜tij≤τ时，部件服从第一阶段的退化过程，其性能变化量服从参数为μ1△tij，λ1的逆高斯分布，不失一般性，部件的失效概率密度函数为f1（△xij，μ1△tij，λ1），则其似然函数为：

（1）当τ＜tij时，部件服从第二阶段的退化过程，其性能变化量服从参数为μ2△tij，λ2的逆高斯分布，不失一般性，部件的失效概率密度函数为f2（△xij，μ2△tij，λ2），则其似然函数为：

4 应用实例

对某型空空导弹引信电容测试数据进行分析获得如图1所示变化曲线图。

图1 某型空空导弹引信电容性能退化量变化曲线

根据某型空空导弹引信电容器性能退化曲线可以看出，在贮存过程中电容器容值随着贮存时间的增加其性能退化率会出现改变，由于贮存环境中不同应力的共同作用使得引信电容器的退化过程呈现两阶段的变化趋势，根据第2节介绍的方法建立某型空空导弹引信电容器退化模型。

相邻测试区间内，第一阶段引信电容值退化增量为：

相邻测试区间内，第二阶段引信电容值退化增量为：

代入似然函数对其取对数，另其偏导为0，选取MCMC（马尔科夫链蒙特卡洛方法）方法对λ，μ两参数进行估算，获得参数动态抽样图如图2所示，求得第一阶段λ1，μ1的估计结果如表1所示。

图2 4000次随机抽样参数估计动态轨迹

表1 参数估计结果

代入似然函数对其取对数，另其偏导为0，选取MCMC方法对λ，μ两参数进行估算，获得参数动态抽样图如图3所示，求得第二阶段λ2，μ2的估计结果如表2所示。

图3 4000次随机抽样参数估计动态轨迹

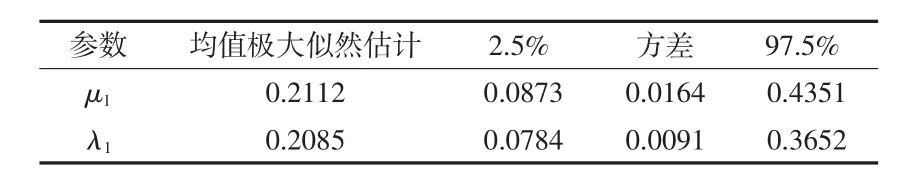
表2 参数估计结果

将λˆ，μˆ代入获得可靠度函数的最大似然估计，选取失效阀值为导弹引信电容器性能退化量≥5F，根据实际测试记录取变点时间为600，即τ＝600，根据第3节公式确定可靠度函数。

实例表明，两阶段退化过程模型可以根据检测数据输出动态轨迹图，直观地得到可靠度的变化规律和预测值，便于空空导弹部件的管理和贮存可靠性预测。

5 结语

空空导弹贮存可靠性是衡量空空导弹武器系统性能的核心指标之一，为了明确空空导弹两阶段性能退化部件可靠性对贮存可靠性的影响，本文结合性能退化的基本理论，利用逆高斯过程（部件的退化过程服从维纳过程时可按照上述方法进行建模求解），对空空导弹部件进行了两阶段退化过程建模，并进行了两阶段退化过程可靠度函数的确定和应用实例的分析。下一步可以继续研究其他部件及环境因素对贮存可靠性的影响，并对已建立的模型进行仿真分析，查找提高空空导弹贮存可靠性的方法和措施。