BDNF基因rs6265多态性与父母教育卷入对小学儿童基本数学能力的交互作用*
张明亮 司继伟 杨伟星 邢淑芬 李红霞 张佳佳
BDNF基因rs6265多态性与父母教育卷入对小学儿童基本数学能力的交互作用*
张明亮1,2司继伟1杨伟星1邢淑芬3李红霞1张佳佳1
(1山东师范大学心理学院, 济南 250358) (2山东行政学院, 济南 250014)(3首都师范大学心理系, 北京市“学习与认知”重点实验室, 北京 100048)
数学能力发展的遗传机制日益成为研究者关注的前沿课题之一, 但既有研究尚处于起步阶段。本研究以602名小学儿童及其父母作为被试, 旨在考察BDNF基因rs6265多态性与父母教育卷入对儿童基本数学能力的潜在交互影响。结果显示, (1) rs6265多态性可显著预测儿童的逻辑思维与空间−视觉功能领域能力(AA基因型携带者的基本数学能力显著高于G等位基因携带者); (2) rs6265多态性与父母教育卷入交互作用于儿童的逻辑思维与空间−视觉功能领域能力, 父母教育卷入能显著正向预测G等位基因儿童的逻辑思维与空间−视觉功能领域能力, 但对AA基因型儿童的预测作用不显著, 该交互作用可能更加符合强素质−压力模型假说(rs6265位点G等位基因可能是风险基因)。上述发现推进了数学能力遗传机制的研究, 并为素质−压力假说提供了新的研究证据。
BDNF基因rs6265多态性; 数学能力; 父母教育卷入; 基因与环境交互作用; 小学儿童
1 引言
现代社会, 数学能力对个人事业成功的影响越来越重要(Siegler & Braithwaite, 2017)。在控制了家庭社会经济地位、智力、受教育年限等因素的前提下, 个体7岁时的数学能力仍能预测其42岁时的社会经济地位(Ritchie & Bates, 2013)。对于数学能力的组成成分, 目前相关研究并未形成一致的标准。国内学者普遍认为, 数学能力的成分包括运算能力、逻辑思维能力和空间想象能力, 其中逻辑思维能力是数学能力的核心(林崇德, 2003; 李丽, 2005)。传统的中小学数学教学大纲也把数学能力分为运算能力、逻辑思维能力、空间想象能力、运用数学知识分析和解决实际问题的能力。数学能力受先天遗传与后天教养(环境)的共同影响(Grasby, Coventry, Byrne, Olson, & Medland, 2016), 揭示数学能力的遗传力(个体的表现型差异可以归因于遗传差异的比率)以及与数学能力相关的具体基因或基因组, 探讨先天遗传与后天教养(环境)对数学能力发展的影响等问题日益成为研究者关注的前沿课题之一。
近年来, 行为遗传学的兴起为揭示数学能力的遗传机制提供了有力支持, 开启了新的研究思路。行为遗传学的发展经历了定量遗传学和分子遗传学两个阶段。定量遗传学的相关研究显示, 数学能力的遗传力在0.2~0.9之间(Kovas, Haworth, Dale et al., 2007), 数学学习困难由遗传(40%~70%)和环境因素(10%~70%)共同决定(Kovas, Haworth, Harlaar et al., 2007)。这些发现为“数学能力的起源与发展存在先天遗传因素”这一观点提供了充分证据。此外, 也有定量遗传学研究对数学能力的成分开展研究。如Hart, Petrill和Thompson (2010)发现, 概念量化(Quantitative Concepts)、应用题(Applied Problems)、计算(Calculation)和流畅性(Fluency)四种数学成分的遗传力存在差异, 分别是0.49、0.41、0.35和0.34, 概念量化和应用题具有稍高的遗传力; 结果还显示, 共享环境因素影响不同数学成分的估计值介于0.32至0.46之间, 明显高于另一项同年龄被试研究(Kovas, Haworth, Petrill, & Plomin, 2007)的估计值(0.07~0.23), 然而, 非共享环境因素的影响(0.19~0.25)则低于Kovas, Haworth, Petrill等人(2007)的估计值(0.42~0.48)。数学能力领域的分子遗传学研究尚处于起步阶段, 相关研究仅见于少数几篇文献, 不仅零星分散不成系统, 而且至今没有学界公认的候选基因(Docherty, Kovas, & Plomin, 2011)。目前, 研究者仅围绕少数几个基因开展了探索性研究, 比如, Myosin-18B (Ludwig et al., 2013)、COMT和BDNF (González-Giraldo et al., 2014)、Del22q11.2 (Carvalho et al., 2014)、KIAA0319和ROBO1 (Mascheretti et al., 2014)、DCDC2和DYX1C1 (Marino et al., 2011)、SPOCK1 (Chen et al., 2017)。也有少量的全基因组关联分析研究(genome- wide association study, GWAS) (Chen et al., 2017; Docherty et al., 2010; Davis et al., 2014; Zhu, Chen, Moyzis, Dong, & Lin, 2015)和单核苷酸多态性(single nucleotide polymorphism, SNP)组合研究(Docherty et al., 2011)。其中, González-Giraldo等人(2014)进行的研究是迄今为止仅见的考察BDNF基因rs6265多态性与简单算术加工关系的研究。他们采用具有欧洲和印第安人融合遗传背景的哥伦比亚波哥大市的大学生(平均年龄21.2岁)作为被试, 发现与GG基因型相比, A等位基因携带者的算术成绩更好。BDNF基因(人类的BDNF基因位于第11号染色体短臂1区3带上, 包含11个外显子)调控脑源性神经营养因子(brain-derived neurotrophic factor)的表达, 其rs6265多态性影响脑源性神经营养因子的水平(Elfving et al., 2012)。而脑源性神经营养因子与神经元的生长、发育、分化、维持、损伤修复以及学习和记忆存在密切关系。BDNF基因A等位基因与脑源性神经营养因子的分泌减少和活性降低有关(González-Castro et al., 2015), 携带A等位基因个体的海马神经元突触复杂性较低、突触可塑性较差、工作记忆得分较低(Miyajima et al., 2008)、记忆功能下降(Cao et al., 2016)。由此可以看出, rs6265多态性与个体的认知能力关系密切, 不同种族不同年龄不同研究设计条件下, rs6265多态性与数学能力是否仍然存在关联是我们考察的目的之一。
尽管数学能力是一种高度遗传的性状, 但是其遗传基础并非单独发挥作用, 而是在与环境因素的互动中不断发生变化。因此, 遗传的影响可以通过环境来调节。在数学能力上, 约有40%的个体差异是由环境因素造成的(Tosto, Haworth, & Kovas, 2015),遗传基础只是给数学能力后天的发展提供了前提(周欣, 康丹, 2015)。生态系统理论认为儿童青少年的发展(如, 数学能力发展)受环境系统的影响, 该理论强调儿童青少年嵌套于一系列相互影响的环境系统(微观系统、中间系统、外层系统、宏观系统)之中。其中, 微观、中间和外层系统都与父母教育卷入直接关联, 父母教育卷入是指父母卷入子女的教育与学习活动(Seginer, 2006); 微观系统的核心就是基于家庭的父母教育卷入。因此, 父母教育卷入, 作为影响儿童青少年发展(如, 数学能力发展)的重要环境因素之一, 引起学界的广泛关注。大量研究为父母教育卷入与儿童青少年学业成绩呈显著正相关提供了坚实的证据支持(Castro et al., 2015; Fan, 2001; Seginer, 2006)。Keith等(1993)进一步发现父母教育卷入与数学学科成绩存在较高正相关, Fan (2001)则发现父母教育卷入与数学学科成绩之间的相关为0.18。
综上所述, 数学能力受先天遗传与后天教养(环境)的共同影响。因此, 对基因与环境交互作用(G×E)机制的探讨具有极为重要的意义(Halldorsdottir & Binder, 2017)。理论层面上, 交互作用机制的揭示可能有助于阐明“假定某些环境因素主效应缺失条件下的状况”; 实践层面上, 通过对交互作用更深入的理解可以促进针对个体不同基因型的有效环境干预策略的发展(Docherty et al., 2011)。近年来, 复杂行为特征发展研究领域对G×E交互作用实质的研究兴趣日益凸显(Caspi & Moffitt, 2006)。一些研究者开始运用定量遗传学的双生子研究范式考察G×E交互对数学能力的影响(Grasby et al., 2016), 并取得了一些有意义的发现。Docherty等人(2011)开展了数学认知领域迄今为止仅见的采用G×E交互设计的分子遗传学研究。他们发现, 数学相关的基因(10个SNP组合:rs11225308、rs363449、rs17278 234、rs11154532、rs12199332、rs12613365、rs6588923、rs2300052、rs6947045和rs1215603)与环境因素(家庭混乱、父母消极、教师消极)之间存在显著交互作用(该交互作用符合素质−压力模型假说), 家庭混乱/父母消极/教师消极均显著反向预测低SNP组合分儿童的数学能力, 对高SNP组合分儿童的数学能力预测作用则不显著。
关于G×E交互作用的理论模型, 目前主要存在“素质−压力模型(diathesis-stress model)”和“差别易感性模型(differential susceptibility model)”两种理论假说。传统的素质−压力模型认为, 当处于不利成长环境时, 那些携带“风险等位基因”/“不良遗传素质”的个体更容易产生心理或行为问题; 但是, 当处于良好成长环境时, 携带不同基因型的个体其发展模式则较为相似。新近兴起的差别易感性模型则认为, 同一(易感性/可塑性)基因型既能够令个体在遭受不利成长环境时变得“更坏”, 也可以在良好环境下变得“更好” (Belsky & Pluess, 2009)。Widaman等人(2012)提出的再参数化回归模型则进一步将G×E交互理论假说细分为“强”/“弱”素质−压力模型或差别易感性模型(Belsky, Pluess, & Widaman, 2013)。具体来说, “强”素质−压力模型或差别易感性模型假设携带“非风险/非可塑等位基因”的个体不受环境的影响; 但是“弱”素质−压力模型或差别易感性模型则假设携带“非风险/非可塑等位基因”的个体也受环境的影响, 只不过所受程度比“风险/可塑等位基因”要低。
鉴于此, 本研究采用G×E交互设计, 综合运用传统的分层回归和新兴的再参数化回归方法, 以3~6年级小学儿童为被试, 以BDNF基因rs6265多态性为遗传指标, 父母教育卷入为环境指标, 系统考察遗传基因与环境对小学儿童基本数学能力的作用, 拟解决的主要问题包括:(1) rs6265多态性是否与小学儿童基本数学能力存在关联; (2) rs6265多态性与父母教育卷入是否对小学儿童基本数学能力存在显著的基因与环境交互作用; (3)如果基因与环境交互作用显著, 是符合素质−压力模型假说还是差别易感性模型假说, 是符合“强”素质−压力模型/差别易感性模型假说还是“弱”素质−压力模型/差别易感性模型假说。
2 研究方法
2.1 被试
选取山东省潍坊市某九年一贯制学校4个年级(三、四、五、六年级)23个班级的602名小学生及其父母作为被试。施测前, 由数学老师或班主任对学生进行评定, 将存在感官缺陷、可能存在情绪困扰、学习动机低、单亲家庭、近期数学成绩有较大波动的儿童及其父母排除; 数据分析前, 将智力落后、数据不完整(父母教育卷入、小学生基本数学能力)、DNA分型失败的儿童及其父母排除。最终获得有效儿童被试527人(平均年龄10.7±1.00岁), 有效父母亲被试1054人, 其中父亲/母亲受教育水平为小学者占10.80% / 25.80%、初中者占70.60% / 56.70%、高中或中专者占13.00% / 10.80%、大专或大学本科者占5.00% / 4.60%、研究生(硕士、博士)者占0.60% / 2.00%。本研究经过山东师范大学伦理委员会审核并获得批准。
2.2 研究工具
2.2.1 瑞文标准推理测验
采用张厚粲和王晓平(1989)修订的《瑞文标准推理测验》考察儿童的一般推理能力。测验共由60张图片组成, 分为5个系列。答对1题计1分, 总分60分, 然后依据年龄和常模转换为标准分, 标准分低于5的视为智力缺陷。
2.2.2 小学生基本数学能力
采用李丽(2005)编制的《中国小学生基本数学能力测试量表(C-RSPMA)》测评小学生基本数学能力。该量表在《德国海德堡大学小学生数学基本能力测试量表》基础上修订完成。量表包含“数学运算领域(MT1)”和“逻辑思维与空间−视觉功能领域(MT2)”两个成分, 共由1个热身测试和11个分测试组成。“抄写数字”属于热身测试, 不计算成绩, 目的是让小学生尽快适应测试气氛并掌握测试方法; MT1由6个分测试组成, 分别是“加法”、“减法”、“乘法”、“除法”、“填空”和“大小比较”, 目的是评定小学生的数学概念、运算速度和计算的准确性; MT2由5个分测试组成, 分别是“续写数字”、“长度估计”、“方块记数”、“图形记数”和“数字连接”, 目的是评定小学生的数学逻辑思维、数字规律识别、空间立体思维和视觉跟踪能力。MT1三、四、五、六年级的内部一致性信度分别为0.88、0.88、0.89、0.88; MT2的则为0.72、0.72、0.72、0.71。后续探索性和验证性分析均采用小学生基本数学能力两成分的标准化得分, 取值范围分别是−2.92~ 2.52 (MT1)、−3.10~2.83 (MT2)。
2.2.3 父母教育卷入
采用吴艺方、韩秀华、韦唯和罗良(2013)编制的《小学生父母教育卷入行为问卷(父母回答版)》测评父亲/母亲教育卷入水平。由父亲、母亲单独填写。父亲/母亲教育卷入问卷均由29个题目组成(共包含“家庭监控”、“学业辅导”、“亲子沟通”、“共同活动”和“家校沟通”5个维度)。采用4点计分——1分(很不赞成)、2分(不同意)、3分(同意)、4分(很同意)。父亲/母亲教育卷入总分均介于29~116分之间, 得分越高表明父亲/母亲教育卷入程度越高。我们将父亲与母亲教育卷入得分相加后除以2作为父母教育卷入得分, 后续探索性和验证性分析则采用父母教育卷入的标准化得分(取值范围是−3.15~ 1.691)。问卷内部一致性信度为0.91, 结构效度良好(c2= 683.82,= 367,0.001, RMSEA = 0.04, CFI = 0.92, SRMR = 0.05, TLI = 0.91)。
2.3 施测程序
以602名小学生及其父母作为测查对象, 向学生及其父母发放参与本研究的知情同意书, 在取得他们同意的前提下, 分4个阶段完成测评。首先, 以班级为单位收集儿童的智力数据。其次, 在学校配合下以班级为单位组织儿童父母到学校参与问卷调查获得父母教育卷入数据。再次, 以班级为单位收集儿童基本数学能力数据。以上三个阶段施测时, 每个班级均由至少2名经过严格培训且具有丰富经验的心理学专业研究生担任主试, 各阶段的施测过程分别是智力数据约40 min、父母教育卷入数据约25 min、儿童基本数学能力数据约60 min, 施测结束后当场回收问卷。最后, 以班级为单位, 经由严格培训的专业人员和研究生采集儿童的唾液样品, 三、四年级主试与儿童的比例不小于1:6, 五、六年级的比例不小于1:8, 班内所有参与测查儿童同步采集唾液样品, 采集过程约30 min。提前请班主任告知所有需要采集唾液的儿童在采集前的30 min不要进食、饮水、嚼口香糖、吸烟、饮酒。由专业公司进行DNA的提取、纯化和分型。
2.4 共同方法偏差的控制
本研究在研究设计与测量过程中采取控制措施, 在数据分析前, 对共同方法偏差进行统计检验, 以控制共同方法偏差效应。测量过程中的控制措施包括:(1)各问卷(量表)的施测在时间上分离, 避免同时集中施测多份问卷(量表); (2)各问卷的指导语、题目计分的编排方式不同; (3)父母教育卷入问卷施测时, 父亲母亲在不同教室进行, 从而实现空间上的分离; (4)选取的问卷(量表)均为信效度较高的成熟问卷(量表); (5)采用严格合理的施测程序减小被试对测量目的的猜度和猜测反应定势。数据分析前, 采用Harman单因子检验对共同方法偏差进行估计。探索性因素分析显示, 特征值大于1的公因子共有15个, 第一个因子解释的变异量为24.25%, 小于40%的临界标准, 表明共同方法偏差不明显。
2.5 数据处理与分析
描述性分析:运用SPSS 19.0进行数据处理和分析, 计算父母教育卷入与儿童基本数学能力两成分的平均数和标准差, 采用皮尔逊积差相关考察变量间的关联程度。进行相关分析时, 对rs6265多态性(GG/AG型=0, AA型=1) (Chen, Li, & McGue, 2013)与性别(男=1, 女=0)作虚拟编码处理。同时为保证分析结果的可靠性, 首先, 对父母教育卷入与儿童基本数学能力各测量指标的性别差异、基因型差异进行独立样本检验, 对年级差异进行单因素方差分析; 其次, 对基因型分布与年级、性别的关联程度, 以及性别与年级的关联程度进行卡方检验, 上述结果与皮尔逊积差相关结果无实质性差异。
探索性分析2:采用分层回归分析rs6265多态性与父母教育卷入对儿童基本数学能力两成分的交互作用。
验证性分析:运用SAS、R和SPSS统计软件, 采用再参数化回归考察基因多态性与父母教育卷入对MT2的交互作用(Widaman et al., 2012; 曹丛等, 2016)。模型示例如下:
其中,为因变量, 也就是MT2;代表不同基因型亚组,= 1代表非风险/非可塑基因型亚组(本研究中为AA基因型),= 2代表风险/可塑基因型亚组(本研究中为G等位基因);1表示父母教育卷入;3表示控制变量年级;4表示控制变量智商;1为“非风险/非可塑基因型”亚组中父母教育卷入对因变量的回归系数;2则是“风险/可塑基因型”亚组中父母教育卷入对因变量的回归系数;3和4分别为控制变量年级、智商对因变量的回归系数;是两基因型亚组斜率的交叉点。
如果的点估计限定于环境变量(父母教育卷入)的最大值处时模型拟合最佳, 则表明rs6265多态性与环境变量的交互作用是“按序型”, 也就是符合素质−压力假说; 如果的点估计和置信区间均落在环境变量取值范围内时模型拟合最佳, 表明基因与环境变量的交互作用是“交叉式”, 也就是符合差别易感性假说(Widaman et al., 2012; 曹丛等, 2016)。在上述两个模型中, 如果将1限定为0(即非风险/非可塑基因型亚组根本不受父母教育卷入等环境变量的影响), 表明强素质−压力/强差别易感性模型成立; 如果取消“1= 0”这一限定(即非风险/非可塑基因型亚组同样受到父母教育卷入等环境变量的影响, 只不过受影响程度小于风险/可塑基因型亚组), 则表明弱素质−压力/弱差别易感性模型成立。
3 结果分析
3.1 Hardy-Weinberg平衡的吻合度检验
采用SHEsis对rs6265位点进行Hardy-Weinberg平衡吻合度检验。结果显示, 该位点基因型(AA、GG、AG)的观察值与期望值吻合良好, 符合Hardy- Weinberg平衡定律(c2= 0.10,= 1,> 0.05)。在后续分析中, 本研究将GG和AG基因型进行了合并(Chen et al., 2013)。
3.2 描述性分析
如表1所示, 年级与因变量MT2呈显著负相关, 在后续的分层回归分析中将年级作为协变量加以控制; 基因型的分布与年级无关; 性别与父母教育卷入呈显著负相关, 父母对女孩的教育卷入显著高于男孩; rs6265基因型的分布与儿童基本数学能力两成分均呈显著正相关(AA基因型携带者显著高于G等位基因携带者); 父母教育卷入与儿童基本数学能力两成分均呈显著正相关。rs6265多态性与父母教育卷入相关不显著, 表明可以排除基因−环境相关的可能性。基因型分布与数学能力(MT2)之间的关系见图1。
3.3 探索性方法考察rs6265多态性与父母教育卷入对儿童基本数学能力两成分的交互作用
以儿童基本数学能力两成分(MT1和MT2)为因变量, 年级、智商作为第一层预测变量(控制变量), rs6265多态性、父母教育卷入作为第二层预测变量, 第二层预测变量之间的交互项作为第三层预测变量进行分层回归分析。结果显示(见表2), rs6265多态性可显著预测MT2 (AA基因型携带者的基本数学能力显著高于G等位基因携带者); 父母教育卷入能够显著正向预测MT1和MT2; rs6265多态性与父母教育卷入对MT2具有显著交互作用, 进一步分析表明, 父母教育卷入显著正向预测G等位基因MT2 (β = 0.16,= 3.27,< 0.01), 对AA基因型的预测作用则不显著(β = −0.13,= −1.39,> 0.05)。
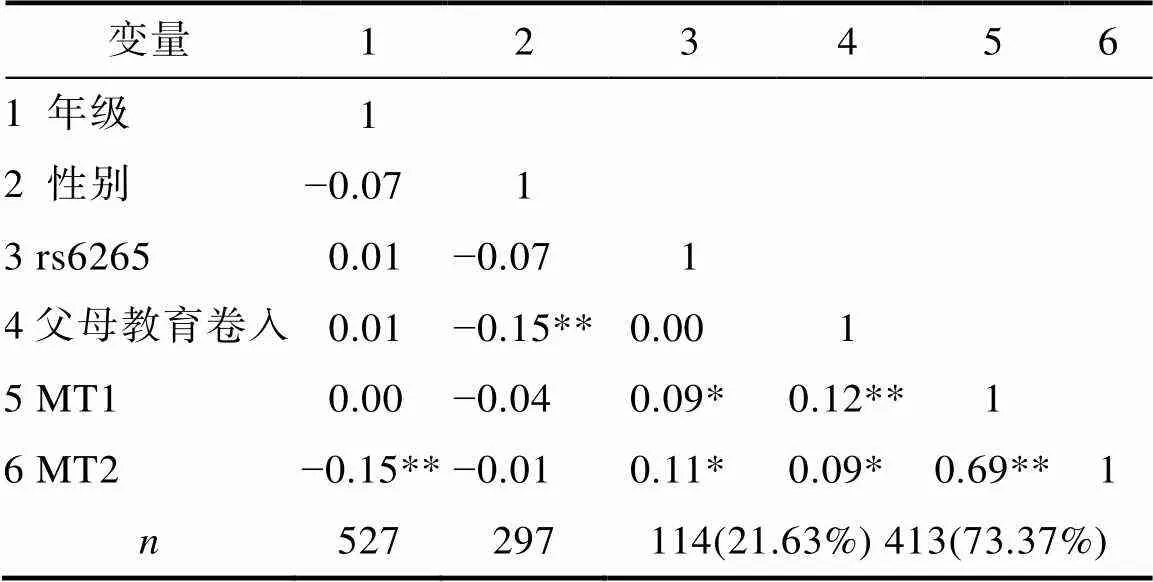
表1 年级、性别、基因多态性、父母教育卷入与儿童基本数学能力两成分的描述统计量及相关分析结果
注:*< 0.05, **< 0.01;分别表示被试总人数、男生人数、AA基因型携带者的人数及比例、G等位基因(GG与AG基因型的合并)携带者的人数及比例; MT1为数学运算领域能力、MT2为逻辑思维与空间−视觉功能领域能力。

图1 不同基因型逻辑思维与空间−视觉功能领域能力(MT2)的人口金字塔图

表2 儿童基本数学能力两成分对rs6265多态性与父母教育卷入的分层回归分析
注:*<0.05, **<0.01。a代表交互作用值经过顺序性Bonferroni检验矫正后仍然显著(Benjamini & Hochberg, 1995)。
3.4 验证性方法考察rs6265多态性与父母教育卷入对逻辑思维与空间−视觉功能领域能力(MT2)的交互作用
根据前述探索性结果, 可假设G等位基因是风险(素质−压力模型假说)/可塑(差别易感性模型假说)等位基因, AA基因型则是非风险(素质−压力模型假说)/非可塑(差别易感性模型假说)基因型3。通过建构再参数化回归模型, 考察rs6265多态性与父母教育卷入对MT2的交互作用, 进而检验强/弱素质−压力模型与差别易感性模型假说。
对rs6265多态性与父母教育卷入对MT2的交互作用进行检验(见表3)。强素质−压力模型(模型c)假设, 当个体遭受不利环境(较低水平的父母教育卷入)时, 携带风险等位基因(G等位基因)的儿童更容易产生问题(较低水平的MT2), 但携带非风险基因型(AA基因型)的儿童则不受此不利环境的影响; 然而, 在良好环境下(较高水平的父母教育卷入), 携带不同基因型的儿童其MT2则较为相似。模型c总体模型显著(2= 0.17,< 0.001), 在限定1= 0 (限定AA基因型不受父母教育卷入的影响)并且将交叉点限定于父母教育卷入的最大值 (父母教育卷入= 1.69)的情况下, 父母教育卷入可以显著正向预测G等位基因儿童MT2 (2= 0.15,= 0.04,= 3.86,< 0.001), 表明rs6265多态性与父母教育卷入对MT2存在显著交互作用。上述证据表明强素质−压力模型拟合良好。
然而, 在判定rs6265多态性与父母教育卷入交互作用符合强素质−压力模型(模型c)之前, 需通过检验与、值判断模型c是否是最佳模型, 也就是模型c比模型a、b、d的拟合性更好。在模型c基础上, 取消1= 0的限定就是模型d(弱素质−压力模型), 取消将交叉点限定于父母教育卷入最大值就是模型a(强差别易感性模型), 同时取消1= 0和将交叉点限定于父母教育卷入最大值就是模型b(弱差别易感性模型), 因而模型c与模型a、b、d之间存在嵌套关系, 可通过检验比较增加一个或两个估计参数时, 模型a、b、d解释的变异量是否比模型c有显著增加。我们发现, 尽管模型a、b、d比模型c多了一个或两个估计参数, 但模型a、b、d并未导致变异量的显著增加(模型a: Δ2= 0.00,> 0.05; 模型b: Δ2= 0.00,> 0.05; 模型d: Δ2= 0.00,> 0.05), 因而无法拒绝模型c。此外, 模型c的和值比其它模型都低(和值越低表明模型拟合性越好)。综上, 与模型a、b、d相比, 模型c的拟合性最好, 即, rs6265多态性与父母教育卷入对MT2的交互作用可能更加符合强素质−压力模型, G等位基因是风险等位基因, AA基因型是非风险基因型。
4 讨论
如前所述, 探讨遗传基因与环境因素的作用机制是当前数学认知领域的重要前沿课题。本研究采用G×E交互设计, 以3~6年级小学儿童为被试, 首次探索性考察了rs6265多态性与父母教育卷入对儿童基本数学能力的影响, 并综合运用传统的分层回归和新兴的再参数化回归模型检验系统考察基因(rs6265多态性)与环境(父母教育卷入)间的交互作用是符合素质−压力模型假说还是符合差别易感性模型假说。

表3 rs6265多态性与父母教育卷入对MT2交互作用的再参数化回归模型检验
注:模型MT2= (rs6265 = AA) (0+1(X父母教育卷入-)) + (rs6265 = GG/AG) (0+2(X父母教育卷入-)) +3X3+4X4+;为两基因型亚组斜率的交叉点;= 置信区间;a代表该参数限定在指定数值上, 其中等于1.69表示将交叉点固定在父母教育卷入的最大值处,1= 0表示非风险/非可塑基因型中其父母教育卷入对MT2无预测作用, 这也是强素质−压力假说和强差别易感性假说的假定条件之一;vs.代表其他嵌套模型与模型c之间的检验, 同理,vs.则代表其他嵌套模型与模型d之间的检验; *< 0.05, **< 0.01, ***< 0.001。
研究结果显示, rs6265多态性可显著预测儿童MT2, AA基因型携带者的MT2显著高于G等位基因携带者, 这与González-Giraldo等人(2014)的研究结果(A等位基因携带者的算术成绩高于GG基因型)基本一致。然而, 本研究以及González- Giraldo等人的结果似乎又与以往研究结果(A等位基因携带者的工作记忆得分较低、记忆功能下降)不太一致。因为一般来说工作记忆得分较低、记忆功能下降将导致较低水平的数学能力。由于数学认知领域对遗传基因与环境因素作用机制的探讨尚处于起步阶段, 既有研究尚未具体阐明上述作用机制, 不过这一不太一致的结果似乎得到了遗传领域部分研究证据的间接支持:(1)研究设计的不同可能导致结果的不同(田相娟, 王美萍, 2016), 比如, 考察BDNF基因与抑郁直接关联的绝大多数研究认为A等位基因是风险基因(Lee et al., 2013; Pei et al., 2012), 而采用G×E交互设计的研究则认为G等位基因可能是易感基因(Zhang et al., 2016); (2)研究对象种族背景的不同可能也会导致结果的不同, 以亚洲人为被试的研究发现, G等位基因携带者更易受压力性生活事件的影响进而表现出更高水平的抑郁(Chen et al., 2013), 而以高加索人为被试的研究则发现, A等位基因携带者在经历压力性生活事件后患抑郁的风险更高一些(Gatt et al., 2009), 这可能是由于不同种族在BDNF基因rs6265多态性频率分布上的不同(亚洲人A等位基因频率约为40%~50%, 高加索人则仅为25%~31%)导致的(田相娟, 王美萍, 2016)。
本研究结果还显示, rs6265多态性与父母教育卷入对儿童MT2具有显著交互作用, 进一步分析显示, 父母教育卷入显著正向预测G等位基因儿童MT2, 而对AA基因型儿童的预测作用则不显著, 该G×E交互作用可能更加符合强素质−压力模型假说, rs6265位点G等位基因可能是风险基因, 携带G等位基因的儿童当遭受较低水平的父母教育卷入时更易获得较低水平的MT2, 但当处于较高水平的父母教育卷入时, 携带不同基因型儿童的MT2则较为相似。本研究首次将数学能力具体成分MT2作为独立研究对象, 目前尚未有更直接证据阐明本研究发现的rs6265多态性与父母教育卷入对MT2具有显著交互作用的具体作用机制。有研究发现小鼠海马内脑源性神经营养因子水平与空间学习能力密切相关, 特异性敲除小鼠海马中BDNF基因可损伤其空间学习能力(Heldt, Stanek, Chhatwal, & Ressler, 2007); 相反, 海马中脑源性神经营养因子水平增高的小鼠其空间学习能力则显著提高(Nakajo et al., 2008)。鉴于此, 我们推测携带G等位基因(A等位基因与脑源性神经营养因子分泌减少和活性降低有关)可能诱发脑源性神经营养因子分泌和活性的过度增加/强, 使其携带者可能更容易捕获不利环境(如低水平的父母教育卷入)中的消极信息, 从而增加获得较低水平MT2的风险。然而, 这仅仅是本研究的初步推测, 尚需后续研究的进一步验证。此外, 本研究G×E交互作用可能更加符合强素质−压力模型假说的发现:(1)在理论层面上, 一方面, 拓展和深化了对父母教育卷入的认识, 个体遗传因素应成为父母教育卷入研究的重要领域, 高质量父母教育卷入除了具有“结构化”等六大特征之外, 个体遗传因素的影响也同样值得关注, 另一方面, 深化了对数学能力遗传机制的认识, rs6265多态性不仅与小鼠空间学习能力相关, 更与MT2密切相关, rs6265位点G等位基因可能是风险基因; (2)在实践层面上, 本研究结果(较低水平的父母教育卷入条件下G等位基因携带者更易获得较低水平的MT2, 而较高水平的父母教育卷入条件下不同基因型携带者的MT2则较为相似)较为清晰地指明了有效干预父母教育卷入的具体路径。
与以往研究(González-Giraldo et al., 2014)相比, 本研究主要有5点突破:(1)研究对象种族背景的扩展, González-Giraldo等人采用的是拉美国家哥伦比亚首都波哥大市的居民, 当地居民具有欧洲和印第安人融合的遗传背景, 我们选用的则是中国汉族被试; (2)年龄阶段上的扩展, Perea, Paternina, Gomez和Lattig (2012)认为, 个体在不同年龄阶段的脑源性神经营养因子含量与功能存在差异, 进而导致行为结果的不同, 因而, 被试年龄的不同可能导致研究结果的不同(Nederhof, Bouma, Oldehinkel, & Ormel, 2010), González-Giraldo等人选用的被试是平均年龄21.2岁的大学生, 本研究则将年龄扩展到小学儿童阶段(平均年龄10.70 ± 1.00岁); (3)数学能力具体成分上的扩展, González-Giraldo等人发现rs6265多态性对简单算术的显著影响, 本研究则首次将rs6265多态性的影响扩展到数学能力的具体成分(数学运算领域、逻辑思维与空间−视觉功能领域); (4)研究设计上的进步, González-Giraldo等人仅考察了rs6265多态性对简单算术的直接效应, 但数学是一种生物性次生能力, 数学能力的遗传基础并非单独发挥作用, 而是会在与环境的互动中不断发生变化, 且总是随着其他因素的变化而变化, 遗传基础只是给数学能力后天的发展提供了前提(周欣, 康丹, 2015), 基于此, 本研究采用G×E交互设计, 则具有更高的理论意义和实践价值; (5)统计方法上的进步, 本研究采用了新兴的再参数化回归方法检验G×E交互作用的具体模式, 方法学优势明显, 一方面, 再参数回归方法无需多次检验, 可直接评估与比较符合哪一种假说, 而传统方法则需要多次检验, 多次检验削弱了检验G×E效应的统计检验力(Belsky et al., 2013), 另一方面, 再参数化回归方法进一步将G×E理论假说区分为“强”/“弱”素质−压力模型或差别易感性模型假说(Belsky et al., 2013)。
毋庸讳言, 作为一项探索性研究, 本研究还存在以下不足:(1)受研究经费限制, 样本量相对有限(有效儿童被试527人); (2)采用了横向研究设计, 横断数据在解释变量间关系方面存在一定局限性; (3)本研究将年级作为控制变量, 没有考察年龄的差异, 而Perea等人(2012)曾发现大脑皮层中的脑源性神经营养因子含量具有发展动态性, 个体不同发展阶段的脑源性神经营养因子水平与功能可能存在差异, 因此, 未来的研究可以在动态发展过程中考察脑源性神经营养因子含量对儿童数学能力产生的差异性影响。
5 结论
本研究可得出以下结论:
(1) rs6265多态性可显著预测儿童的逻辑思维与空间−视觉功能领域能力, AA基因型携带者的逻辑思维与空间−视觉功能领域能力显著高于G等位基因携带者。
(2) rs6265多态性与父母教育卷入显著交互作用于逻辑思维与空间−视觉功能领域能力, 父母教育卷入正向预测G等位基因儿童的逻辑思维与空间−视觉功能领域能力, 但对AA基因型儿童的预测作用不显著。
(3) rs6265多态性与父母教育卷入对逻辑思维与空间−视觉功能领域能力的交互作用可能更加符合强素质−压力模型假说, rs6265位点G等位基因可能是风险基因, 携带G等位基因的儿童当遭受较低水平的父母教育卷入时更易导致较低水平的逻辑思维与空间−视觉功能领域能力, 但在面对较高水平的父母教育卷入时, 携带不同基因型/等位基因的儿童逻辑思维与空间−视觉功能领域能力较为相似。
Belsky, J., & Pluess, M. (2009). Beyond diathesis stress: Differential susceptibility to environmental influences.(6), 885–908.
Belsky, J., Pluess, M., & Widaman, K. F. (2013). Confirmatory and competitive evaluation of alternative gene-environment interaction hypotheses.(10), 1135–1143.
Benjamini, Y., & Hochberg, Y. (1995). Controlling the false discovery rate: A practical and powerful approach to multiple testing.(1), 289–300.
Cao, B., Bauer, I. E., Sharma, A. N., Mwangi, B., Frazier, T., Lavagnino, L., ... Soares, J. C. (2016). Reduced hippocampus volume and memory performance in bipolar disorder patients carrying theval66met met allele., 198–205.
Cao, C., Wang, M. P., Ji, L. Q., Wei, X., Cao, Y. M., & Zhang, W. X. (2016). The MAOA rs6323 polymorphism interacts with maternal supportive parenting in predicting adolescent depression: Testing the diathesis-stress and differential susceptibility hypotheses.(1), 22–35.
[曹丛, 王美萍, 纪林芹, 魏星, 曹衍淼, 张文新. (2016). MAOA基因rs6323多态性与母亲支持性教养对青少年抑郁的交互作用: 素质-压力假说与不同易感性假说的检验.(1), 22–35.]
Carvalho, M. R. S., Vianna, G., Oliveira, L. de F., Costa, A. J., Pinheiro-Chagas, P., Sturzenecker, R., ... Haase, V. G. (2014). Are 22q11.2 distal deletions associated with math difficulties?.(9), 2256–2262.
Caspi, A., & Moffitt, T. E. (2006). Gene–environment interactions in psychiatry: Joining forces with neuroscience.(7), 583–590.
Castro, M., Expósito-Casas, E., López-Martín, E., Lizasoain, L., Navarro-Asencio, E., & Gaviria, J. L. (2015). Parental involvement on student academic achievement: A meta-analysis., 33–46.
Chen, H., Gu, X. H., Zhou, Y. X., Ge, Z., Wang, B., Siok, W. T., ... Sun, Y. M. (2017). A genome-wide association study identifies genetic variants associated with mathematics ability., 40365.
Chen, J., Li, X. Y., & McGue, M. (2013). The interacting effect of the BDNF Val66Met polymorphism and stressful life events on adolescent depression is not an artifact of gene–environment correlation: Evidence from a longitudinal twin study.(10), 1066–1073.
Davis, O. S., Band, G., Pirinen, M., Haworth, C. M., Meaburn, E. L., Kovas, Y., ...Spencer, C. C. (2014). The correlation between reading and mathematics ability at age twelve has a substantial genetic component., 4204.
Docherty, S. J., Davis, O. S. P., Kovas, Y., Meaburn, E. L., Dale, P. S., Petrill, S. A., ... Plomin, R. (2010). A genome-wide association study identifies multiple loci associated with mathematics ability and disability.(2), 234–247.
Docherty, S. J., Kovas, Y., & Plomin, R. (2011). Gene-environment interaction in the etiology of mathematical ability using SNP sets.(1), 141–154.
Elfving, B., Buttenschøn, H. N., Foldager, L., Poulsen, P. H. P., Andersen, J. H., Grynderup, M. B., ... Mors, O. (2012). Depression, the Val66Met polymorphism, age, and gender influence the serum BDNF level.(9), 1118–1125.
Fan, X. T. (2001). Parental involvement and students' academic achievement: A growth modeling analysis.(1), 27–61.
Gatt, J. M., Nemeroff, C. B., Dobson-Stone, C., Paul, R. H., Bryant, R. A., Schofield, P. R., ... Williams, L. M. (2009). Interactions between BDNF Val66Met polymorphism and early life stress predict brain and arousal pathways to syndromal depression and anxiety.(7), 681–695.
González-Castro, T. B., Nicolini, H., Lanzagorta, N., López-Narváez, L., Genis, A., Pool García, S., & Tovilla-Zárate, C. A. (2015). The role of brain-derived neurotrophic factor (BDNF) Val66Met genetic polymorphism in bipolar disorder: A case-control study, comorbidities, and meta-analysis of 16,786 subjects.(1), 27–38.
González-Giraldo, Y., Rojas, J., Novoa, P., Mueller, S. T., Piper, B. J., Adan, A., & Forero, D. A. (2014). Functional polymorphisms in BDNF and COMT genes are associated with objective differences in arithmetical functioning in a sample of young adults.(3), 152–157.
Grasby, K. L., Coventry, W. L., Byrne, B., Olson, R. K., & Medland, S. E. (2016). Genetic and environmental influences on literacy and numeracy performance in Australian school children in Grades 3, 5, 7, and 9.(5), 627–648.
Halldorsdottir, T., & Binder, E. B. (2017). Gene × environment interactions: From molecular mechanisms to behavior.(1), 215–241.
Hart, S. A., Petrill, S. A., & Thompson, L. A. (2010). A factorial analysis of timed and untimed measures of mathematics and reading abilities in school aged twins.(2), 63–69.
Heldt, S. A., Stanek, L., Chhatwal, J. P., & Ressler, K. J. (2007). Hippocampus-specific deletion of BDNF in adult mice impairs spatial memory and extinction of aversive memories.(7), 656–670.
Keith, T. Z., Keith, P. B., Troutman, G. C., Bickley, P. G., Trivette, P. S., & Singh, K. (1993). Does parental involvementaffect eighth-grade student achievement? Structural analysis of national data.(3), 474–496.
Kovas, Y., Haworth, C. M. A., Dale, P. S., Plomin, R., Weinberg, R. A., Thomson, J. M., & Fischer, K. W. (2007). The genetic and environmental origins of learning abilities and disabilities in the early school years.(3), i, iii–v, vii, 1–156.
Kovas, Y., Haworth, C. M. A., Harlaar, N., Petrill, S. A., Dale, P. S., & Plomin, R. (2007). Overlap and specificity of genetic and environmental influences on mathematics and reading disability in 10-year-old twins.(9), 914–922.
Kovas, Y., Haworth, C. M. A., Petrill, S. A., & Plomin, R. (2007). Mathematical ability of 10-year-old boys and girls: Genetic and environmental etiology of typical and low performance.(6), 554–567.
Lee, Y., Lim, S. W., Kim, S. Y., Chung, J. W., Kim, J., Myung, W., ... Kim, D. K. (2013). Association between the BDNF val66Met polymorphism and chronicity of depression.(1), 56–61.
Li, L. (2005).(Unpublished doctorial dissertation). Huazhong University of Science and Technology, Wuhan.
[李丽. (2005).(博士学位论文). 华中科技大学, 武汉.]
Lin, C. D. (2003).. Beijing: Beijing Normal University Press.
[林崇德. (2003).. 北京: 北京师范大学出版社.]
Ludwig, K. U., Sämann, P., Alexander, M., Becker, J., Bruder, J., Moll, K., ... Czamara, D. (2013). A common variant in Myosin-18B contributes to mathematical abilities in children with dyslexia and intraparietal sulcus variability in adults., e229.
Marino, C., Mascheretti, S., Riva, V., Cattaneo, F., Rigoletto, C., Rusconi, M., ... Molteni, M. (2011). Pleiotropic effects of DCDC2 and DYX1C1 genes on language and mathematics traits in nuclear families of developmental dyslexia.(1), 67–76.
Mascheretti, S., Riva, V., Giorda, R., Beri, S., Lanzoni, L. F. E., Cellino, M. R., & Marino, C. (2014). KIAA0319 and ROBO1: Evidence on association with reading and pleiotropic effects on language and mathematics abilities in developmental dyslexia.(4), 189–197.
Miyajima, F., Ollier, W., Mayes, A., Jackson, A., Thacker, N., Rabbitt, P., ... Payton, A. (2008). Brain-derived neurotrophicfactor polymorphism Val66Met influences cognitive abilities in the elderly.(4), 411–417.
Nakajo, Y., Miyamoto, S., Nakano, Y., Xue, J.-H., Hori, T., & Yanamoto, H. (2008). Genetic increase in brain-derived neurotrophic factor levels enhances learning and memory., 103–109.
Nederhof, E., Bouma, E. M. C., Oldehinkel, A. J., & Ormel, J. (2010). Interaction between childhood adversity, brain-derivedneurotrophic factor val/met and serotonin transporter promoter polymorphism on depression: The TRAILS study.(2), 209–212.
Pei, Y., Smith, A. K., Wang, Y. J., Pan, Y. L., Yang, J., Chen, Q., ... Ma, X. (2012). The brain-derived neurotrophic-factor () Val66Met polymorphism is associated with geriatric depression: A meta-analysis.(5), 560–566.
Perea, C. S., Paternina, A. C., Gomez, Y., & Lattig, M. C. (2012). Negative affectivity moderated by BDNF and stress response.(3), 767–774.
Ritchie, S. J., & Bates, T. C. (2013). Enduring links from childhood mathematics and reading achievement to adult socioeconomic status.(7), 1301– 1308.
Seginer, R. (2006). Parents' educational involvement: A developmental ecology perspective.(1), 1–48.
Siegler, R. S., & Braithwaite, D. W. (2017). Numerical development.(1), 187–213.
Tian, X. J., & Wang, M. P. (2016). BDNF gene and depression.(10), 1583–1591.
[田相娟, 王美萍. (2016). BDNF基因与抑郁.(10), 1583–1591.]
Tosto, M. G., Haworth, C. M. A., & Kovas, Y. (2015). Behavioural genomics of mathematics. In R. C. Kadosh & A. Dowker (Eds.),(pp. 993–1017). Oxford: Oxford University Press.
Widaman, K. F., Helm, J. L., Castro-Schilo, L., Pluess, M., Stallings, M. C., & Belsky, J. (2012). Distinguishing ordinal and disordinal interactions.(4), 615–622.
Wu,Y. F., Han, X. H., Wei, W., & Luo, L. (2013). Theoretical model construction and testing of parental involvement in primary school children education.(1), 61–69.
[吴艺方, 韩秀华, 韦唯, 罗良. (2013). 小学生父母教育卷入行为理论模型的建构与验证.(1), 61–69.]
Zhang, H. C., & Wang, X. P. (1989). Standardization research on RAVEN’s standard progressive matrices in China.(2), 113–121.
[张厚粲, 王晓平. (1989). 瑞文标准推理测验在我国的修订.(2), 113–121.]
Zhang, L. L., Li, Z., Chen, J., Li, X. Y., Zhang, J. X., & Belsky, J. (2016). The BDNF val66met polymorphism interacts with maternal parenting influencing adolescent depressive symptoms: Evidence of differential susceptibility model.(3), 471–483.
Zhou, X., & Kang, D. (2015).Shanghai: Huadong Normal University Press.
[周欣, 康丹. (2015).上海: 华东师范大学出版社.]
Zhu, B., Chen, C. S., Moyzis, R. K., Dong, Q., & Lin, C. D. (2015). Educational attainment-related loci identified by GWAS are associated with select personality traits and mathematics and language abilities., 96–100.
1实际上, 我们也对父母教育卷入的标准化得分做了偏态转换(平方根转换), 但数据分析(描述性分析、探索性分析、验证性分析)与转换前相比均没有实质性差异。
2实际上, 我们也进行了显著性区域(region of significance, RoS)方法的检验, 并得出了与再参数化回归模型检验一致的结论。
3实际上, 我们也建构了AA基因型为风险/可塑基因型, 但模型拟合度比上述假设的模型拟合性差。
Interaction effects between BDNF gene rs6265 polymorphism and parent-involved education on basic mathematical ability in primary school children
ZHANG Mingliang1,2; SI Jiwei1; YANG Weixing1; XING Shufen3; LI Hongxia1; ZHANG Jiajia1
(1School of Psychology, Shandong Normal University, Jinan 250358, China) (2Shandong Administrative Institute, Jinan 250014, China) (3Beijing Key Laboratory of Learning and Cognition and Department of Psychology, Capital Normal University, Beijing 100048, China)
Mathematics is an essential subject related to many fields such as science, engineering, economics, and medicine, which are of great and increasing importance for the development of modern society. In recent years, many studies using quantitative genetics, which adopted the twin-study design, were conducted to identify the heritability of performance related to mathematical ability and disability. Although the underlying mechanism is poorly understood, the qualitative behavioral genetics study demonstrated that mathematical abilities are moderately heritable. However, extant evidence was mainly obtained from quantitative genetic research, solely reported by a few molecular genetic studies, which specifically investigated mathematical ability or disability. To the best of our knowledge, till date, only a single molecular genetic study has investigated the effect of the gene (G) × environment (E) interactions on mathematical ability in children. The present study was designed to extend the previous research by examining the effect of the interaction between brain-derived neurotrophic factor (BDNF) gene rs6265 polymorphism and parent-involved education (PIE) on the basic mathematical ability in primary school children. Further, we assessed these two competing models, the classic diathesis-stress model. the newly developed differential susceptibility model.
Primary school (PS) children (= 602, male = 297, female = 305) from 23 classes ranging from grade-3 to grade-6 were included in the study. Their basic mathematical ability was assessed using the Chinese rating scale of pupil’s mathematical abilities and PIE was examined by employing a behavior questionnaire of pupil’s PIE (version answered by parents). The genomic DNA of PS children was extracted from their saliva samples. Genotyping of these DNA samples to identify rs6265 polymorphism inwas performed using real-time PCR with MassARRAY RT software version 3.0.0.4 and analyzed using MassARRAY typer software version 4.0. A series of linear regression statistical analyses were conducted using statistical package for social sciences software version 19.0. Further, re-parameterized regression models were constructed to examine the effect of the interaction betweenrs6265 polymorphism and PIE on basic mathematical ability in PS children using the two potential competing G × E hypotheses.
In this study, we obtained three major results, which are as follows: (1)rs6265 polymorphism was significantly associated with logical thinking (LT) and spatial vision (SV) abilities in PS children. Especially, PS children carrying the AA genotype exhibited a better performance of LT and SV abilities compared to PS children carrying the G allele. (2) The interaction between rs6265 polymorphism and PIE substantially predicted LT and SV abilities in PS children. The PIE behavior positively predicted LT and SV abilities among PS children carrying the G allele but not the AA genotype. (3) The indexes in re-parameterized regression models supported the strong diathesis-stress model.
In conclusion, by elaborating the moderating effect of PIE, the present study enriches the literature on the association betweenrs6265 polymorphism and basic mathematical ability in PS children. This study expands our knowledge regarding the G × E underpinnings of basic mathematical ability and the novel as well as newly developed methods, which are proving to be highly efficient and legitimate.
BDNF gene rs6265 polymorphism; mathematical abilities; parent-involved education; gene × environment interaction; primary school children
B844; B845
2017-07-07
* 山东省自然科学基金青年基金项目(ZR2013CQ025)、国家自然科学基金面上项目(31371048)、国家社会科学基金项目(12CYY022)、山东省自然科学基金培养基金项目(ZR2016EEP13)和山东省“十二五”特色重点学科“发展与教育心理学”专项经费资助。
司继伟, E-mail: sijiwei1974@126.com
10.3724/SP.J.1041.2018.01007

