基于相位差的转轴扭矩测量中的零位识别与处理

刘 翔 黄文平 牛慧萍 蔡 萍

(1.上海交通大学，上海 200240; 2.上海航天智能装备有限公司，上海 201114)

1 引 言

扭矩测量与控制在现代智能制造和动力设备监控中扮演越来越重要的角色。不断提高扭矩测量的便利性、实时性和准确性是扭矩测量和监测的不懈追求。目前应用较为成熟的转轴扭矩测量方法主要有应变型、磁弹性和转角型等[1]。应变型扭矩传感器因为结构简单、成本低等优势在国内应用最多，但应用时需要解决旋转条件下的可靠供电和信号传输等问题[2,3]。磁弹性传感器结构上相对复杂，而且为了获得一定精度对传感器相应材料及现场工况有比较严格的要求，因而现场应用较少[4]。转角型测量方法因易于实现非接触测量，可以适应严苛的环境并实现长期可靠工作，因而在长轴系扭矩测量中具有突出优势[5]。基于相位差测量原理是转角型扭矩传感器实现扭矩测量的基本方法，即通过比较同一转轴上不同位置传感器所输出脉冲信号的相位差，结合转轴材料的扭转刚度系数来间接测量施加在转轴上的扭矩载荷。传统的这种测量方法必须在轴系旋转起来后才能进行扭矩测量，不能测试静态载荷。但在实际应用中一些特殊的场合，如舰船螺旋桨主轴、水下航行器等，转轴一旦转动即带上负载，不存在扭矩为零的初始状态，这就给扭矩测量系统的现场安装和调校带来很大不便，限制了这种测量方法的实际工程应用。

针对上述应用的局限性，本文提出了一种新的基于相位差原理的转轴扭矩测量方法和系统，可以自动识别系统零位并加以校正。本文从测试原理、系统实现和实验测试几个方面，对所提出方法的可行性和适应性进行了理论分析和实际验证。

2 测试原理

转轴在扭矩载荷的作用下会产生一定的扭转变形，根据工程力学原理，大小为M的扭矩载荷在转轴轴向距离L上产生的相对扭转变形角θ可表示为

(1)

式中：G——材料的剪切弹性模量;Ip——横截面对圆心的极惯性矩；在转轴材料、界面形状以及轴向距离L确定的情况下，剪切弹性模量G和极惯性矩Ip均为确定的常数，有

M=K×θ

(2)

式中：K——比例系数。因此如果能够得到扭转变形角θ，则可根据式(2)得到扭矩载荷。由于一般转轴都是作为动力传输装置，为了传输足够的功率和工作安全，转轴的扭矩刚度和极惯性矩都很大，导致实际的扭矩变形角非常小，难以直接进行测量。实际应用中的普遍做法是通过如图1所示的测量结构，将转轴的扭矩变形角转换成两路脉冲信号或正弦信号之间的相位差来进行检测[6,7]。

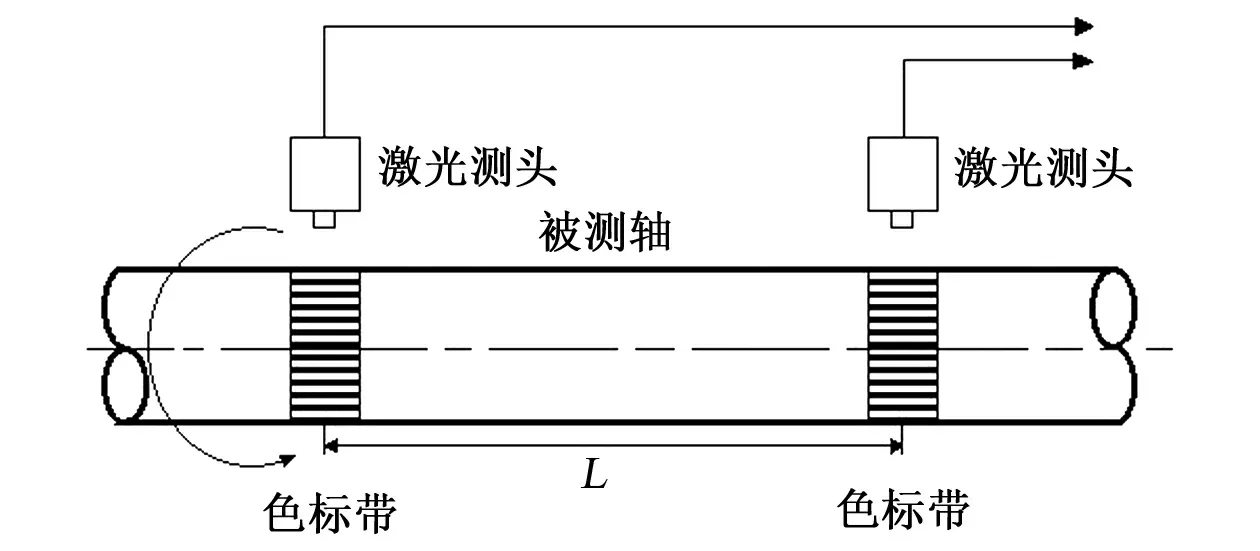
图1 测量结构图Fig.1 Measurement structure

以常用的激光测量系统为例来说明图1所示的测量系统的组成和工作原理。在转轴上距离为L的两处制作反射/不反射(明暗相间)的色标带，在转轴外垂直于色标带固定两个反射式激光光强传感器测头，当转轴转动时，两个激光测头将输出两路同频的高低电平脉冲信号。在一定扭矩载荷作用下，转轴产生扭转变形，导致两路脉冲信号之间产生的相位差产生变化，相位差的变化量与扭矩大小成比例关系，因而可以利用相位差来完成扭矩的测量[8～10]。

上述方案具有简单易行，成本低廉等特点，是目前基于相位差原理的转轴扭矩测量系统实现的普遍方法。但这种方案存在一定的局限性，它必须在轴系旋转状态下才能进行测量，不能测试静态载荷。在没有空载工况的使用中无法进行现场零位调校。同时，由于实际情况中转轴扭矩变形引起的脉冲信号相位差极其微小，机械安装时的初始相位差往往远大于载荷引起的相位差变化，而且难以进行精确控制，这就给扭矩测量系统的现场安装和调校带来很大不便，限制了这种测量方法的实际工程应用。

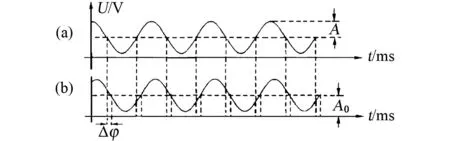
图2 两路正弦信号Fig.2 Two channels of sinusoidal signals

针对这种问题，本文对图1所示的传统测试系统加以适应性改进，采用连续的反射式模拟输出型光强激光测头，配合适当的光学系统和反射色标带宽度，当转轴转动时，激光测头输出如图2所示的连续正弦信号。

正弦信号的幅值与激光测头和色标带的相对位置相对应。当激光测头与亮条纹对应时，输出信号最大值；当激光测头与暗条纹对应时，输出信号最小值。转轴停止转动时，因为激光测头对准固定的色标带位置，输出信号幅度保持不变。因此某一时刻输出信号幅度的大小只与激光测头对准的色标带位置有关，而与测量的时间点没有关系。因此理论上可以通过信号幅度值来确定两路信号的相位差，从而在转轴静止条件就可以确定出两路信号的初始相位差。

采集两个激光测头输出的正弦电压幅度信号，可以利用正弦信号自身的特性来求取相位信息。任意时刻电压瞬时值U与正弦信号峰值A之比取反正弦，就得到该路信号的瞬时相位。瞬时相位变化本质上与旋转位移有关，即与转轴表面绕中心轴转动的总位移有关。因此可以将正弦信号与时间的关系转换成正弦信号与旋转位移的关系，从而可以不用考虑转速等信息对提取相位差的影响。

实际应用中，求出准确的峰值是实现相位差计算的重要部分。因为激光与光标带配合所输出的并不是理想的正弦信号，同时因外界工况影响信号会有毛刺或畸变，在采集到信号之后需要进行对信号进行滤波及正弦拟合处理。在得到光滑的正弦曲线后，再从信号中提取各周期的最大值，求取平均值最终作为信号峰值A。

假设采集得到两路正弦信号Ua和Ub,A为信号的峰值，A0为信号偏置电压，φa和φb分别为此时信号的瞬时相位，在一个周期内可表示为

Ua=A0+A·sinφa

(3)

Ub=A0+A·sinφb

(4)

由式(3)和(4)可得

(5)

(6)

再对两个相位值进行差分，得到两路信号的瞬时相位差Δφ

Δφ=φa-φb

(7)

此相位差反映了转轴上扭转角的大小，从而可以由式(2)得到转轴上的扭矩载荷。

上述测量实现方案不同于传统方法的主要区别在于传感器的输出不是脉冲信号，而是连续的模拟正弦信号，信号幅度与激光测头和色标带的相对位置对应。

所测信号的相位差值主要与转轴两端所产生的扭转角大小有关，同时也与激光测头初始安装位置有关。实际应用中，无法保证两侧的激光测头与色标带安装位置完全一致，因此两路信号初始阶段将输出不同的电压值，信号之间也存在初始相位差，即相位差的零位，如图3所示。初始零位不能忽略，需要准确测量出转轴空载状态的相位差初始零位，才能得到加载后准确的扭矩载荷值。

图3 信号初始零位Fig.3 Zero point of sinusoidal signals

传统脉冲信号相位差测量方法，转轴相位差初始零位需要在转轴不施加扭矩空载转动的情况下来测量。但在实际应用中一些特殊场合被测转轴不存在扭矩为零的空载状态，例如舰船螺旋桨主轴、水下航行器等。因而传统方法无法完成相位差初始零位的测量，此时采用上文测量相位差的方法则可以实现初始零位的识别。转轴静止时，激光测头对准色标带上某个固定位置，输出的稳定值包含了初始零位的信息。而当转轴开始转动后，激光测头将输出两路幅值按正弦规律变化的动态信号。

因此记录转轴初始状态下的两路信号零位电压值，则可按式(5)～式(7)求出两路信号相位差的初始零位φ0

φ0=φa-φb

(8)

3 系统实现

上文提出具有静态零位识别功能的转轴相位差测量的基本原理，在系统实现上则需要结合实际的测试要求(测量对象、量程范围、分辨率)从反射光标带、激光测头、数据采集和信号处理几个方面进行相应的具体设计。

3.1 测试系统结构及关键参数选择分析

测试系统的结构包含如下几个部分：被测轴与光标带、激光测头、信号调理电路、信号采集与处理等几个部分。如图4所示。

图4 测试系统结构Fig.4 Structure of measuring system

光标带及激光传感器在固定安装后均需要进行多次测试和微调，减小机械安装误差。为了得到两路标准的正弦信号，除了要求选用线性度好的激光光强传感器之外，还要合理设计反射光标带宽度和激光光斑大小。在选定反射式激光传感器后，可以通过光学镜头调整激光光斑大小。当光斑相对反射光标带宽度过小或者过大，波形都会发生变形，增大测量误差。在经过现场多次试验后，设定直径略大于反射光标带宽度10%～15%左右，可以得到实验所需的较理想的正弦曲线。本文研究中采用基恩士公司的激光测头KV-NH11。

信号调理和数据采集处理部分主要完成两路激光所输出模拟信号的滤波、放大和同步采集，以及辅助的存储、通讯等功能。本文的信号调理和数据采集处理部分如图5所示。信号采集调理电路采用了多级滤波放大电路实现信号的低通滤波及放大；由ARM控制AD进行同步采集和信号处理、存储通讯。

图5 测量电路框图Fig.5 Structure of measurement circuit

为保证上述数据采集系统可以达到所需的分辨率和精度，同时适应不同转速下的测量需求，需要对所采用AD芯片的参数如采样率和位数进行分析。若已知转轴轴向距离L，材料剪切弹性模量G和轴径D，可以根据式(9)计算施加不同扭矩M时所产生的扭转角α

(9)

由上式可知，对于同一转轴，为提高系统扭矩测量的分辨率，可以增加转轴轴向距离L，增大被测扭转角。同时也可以通过增大AD芯片的位数，提高被测扭转角的分辨率，进而提高所测扭矩的分辨率。

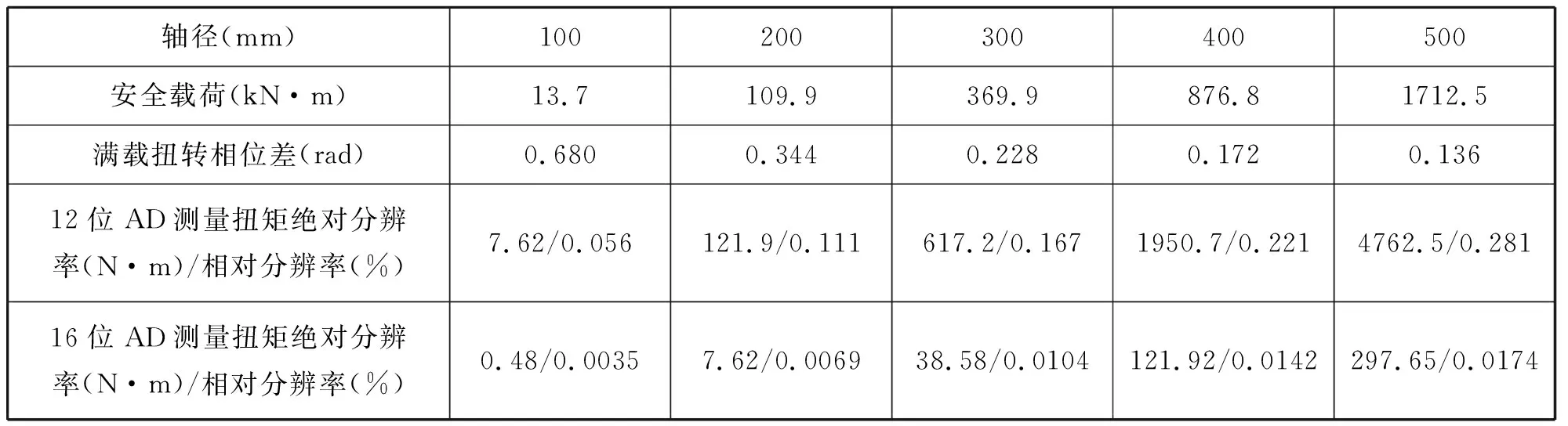
表1 不同轴径及不同AD位数时的扭矩分辨率

由表1可以看出，测量分辨率与轴径和AD位数密切相关，具体应用中可参考本表恰当选择。

另一方面，转轴转速越高，激光测头所输出的正弦信号频率也越高，因此所选用的AD芯片的采样率应能满足不同频率信号的采样要求。因此为了扩大转轴转速适用范围，同时保证测量的准确度，应该提高AD芯片的采样率。本文研究中采用了16位逐次逼近式数模转换芯片AD7656，它具有6个同步采样的模拟通道，每通道的独立采样频率可达250kSPS，最大积分非线性为4LSB，因而可以很好的满足本研究需求。

3.2 模拟标准输入测试

为验证本文相位差Δφ及零位的测试方法，首先采用上述数据采集系统进行模拟标准输入测试。在系统输入端通过两个信号发生器输入两路等幅同频的标准正弦信号，借助信号发生器相位调节功能，手动调整其中一路信号的相位φ，使输入的两路正弦信号之间存在变化的相位差，以此来验证测量系统对相位差及初始零位的测量功能，如图6、图7所示。

由模拟实验测试结果表明，这种测试方法可以测试不同频率或不同变化方式下信号的初始相位及其相位差变化，可以满足实际应用的要求。

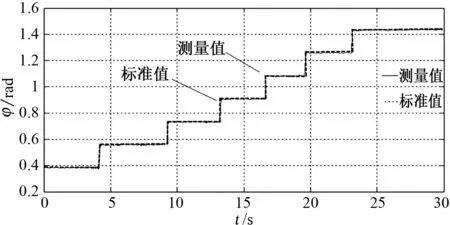
(a) 相位差阶梯变化

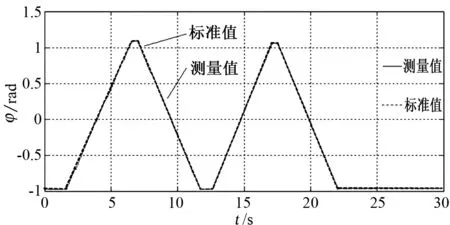
(a) f=20Hz

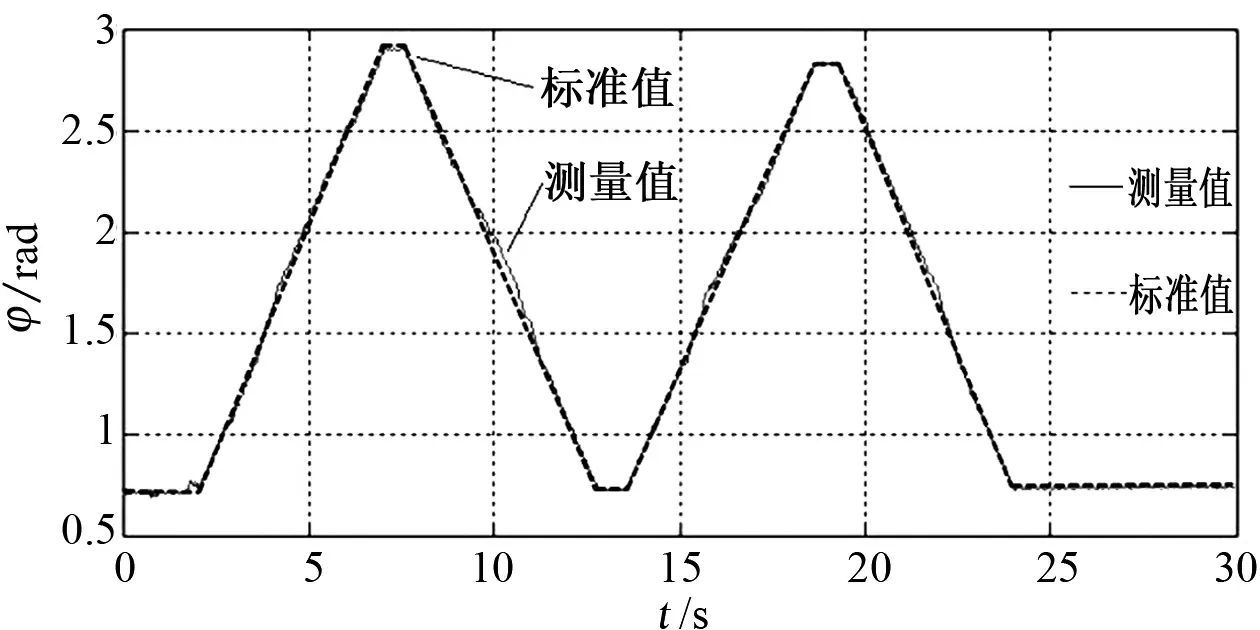
(b) f=40Hz

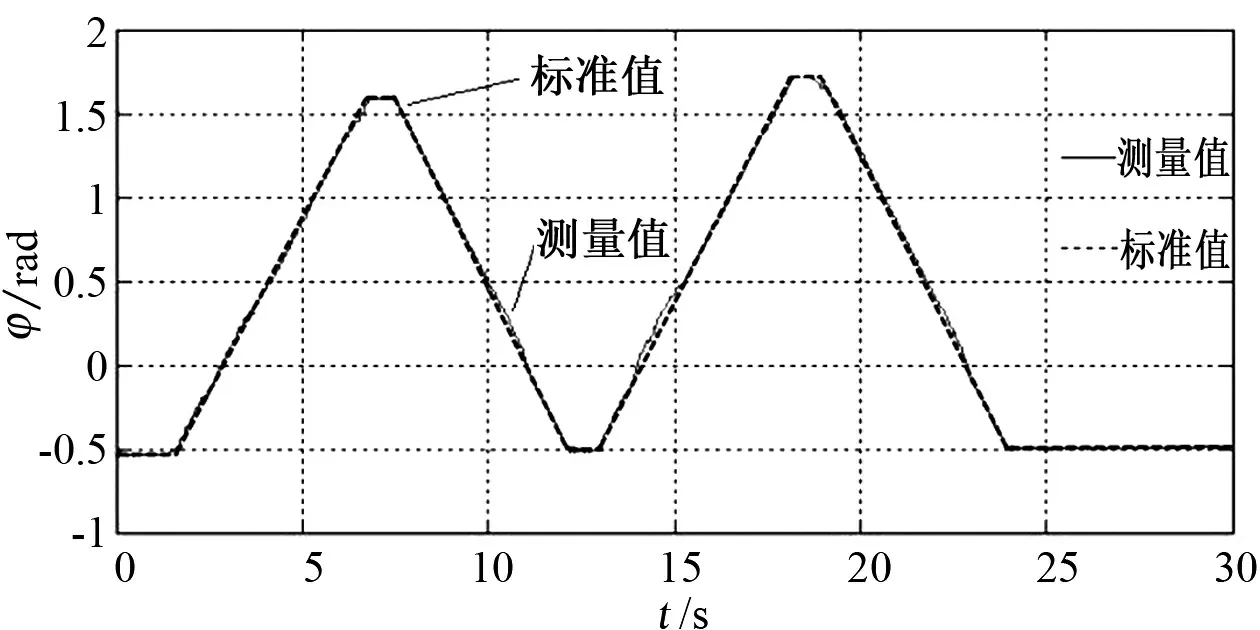
(c) f=60Hz图7 输入不同频率模拟信号相位差按线性递进和递减变化Fig.7 Phase difference of different frequency signals changing linearly

4 转轴扭转变形实际测量实验

为验证上述扭转变形测量的方法，在国防大扭矩一级计量站标准扭矩实验台上进行了实际的验证实验测试。如图8所示，被测转轴轴径D为100mm，剪切弹性模量G约为26GPa，考虑到灵敏度因素以及测量的可靠性，反射式激光测头所在的AB两点的轴向距离L取为800mm。在转轴上AB两端粘贴黑白交错的色标带，每条色标带上设置40组黑白色标条，黑色与白色标带宽度相等。基于检测距离、输出特性等因素，系统选用基恩士公司的激光测头KV-NH11。激光测头所发射的光斑直径需调节至略大于色标条宽度，输出为连续的模拟电压，电压峰值和激光测头与色标带之间距离有关，本文中峰值设置为3V。在进行相位差分析计算之前，需要对输出波形进行预处理，进行滤波及正弦拟合，得到相对平滑的正弦信号曲线。图9显示所输出波形曲线初始阶段。

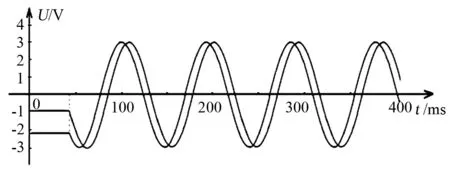
图9 输出波形Fig.9 Output waveforms

受所采用标准扭矩试验台的功率制约，为了达到2000N·m的扭矩载荷，实验中扭矩加载平台的稳定转速控制在27r/min。表2所示为加载不同扭矩时的测量值的平均结果。

实验中重复进行了多次加载、卸载实验，将测量数据平均得到进程及回程曲线如图10所示。

从表2和图10可以看出，在2000N·m量程范围内，根据本文的扭矩测量系统和方法，扭矩测量的精度优于0.5%FS，可以满足工程应用的需要。

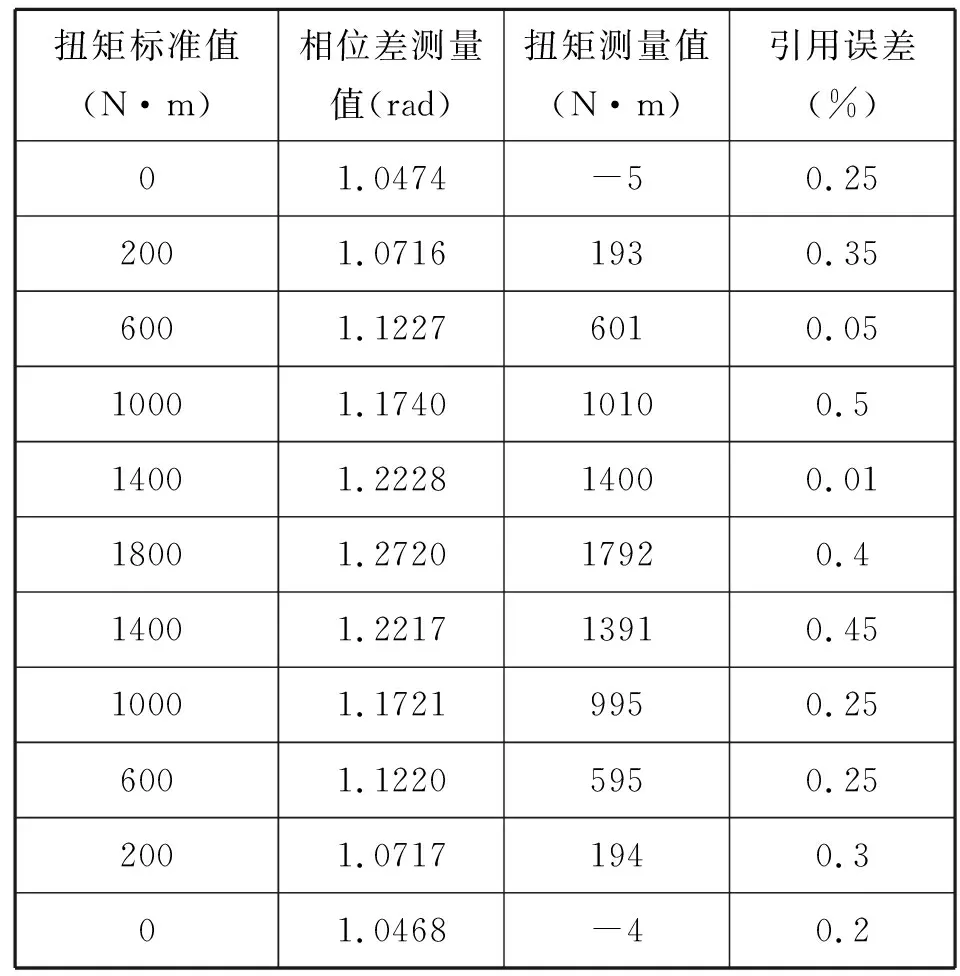
表2 扭矩测量值与引用误差

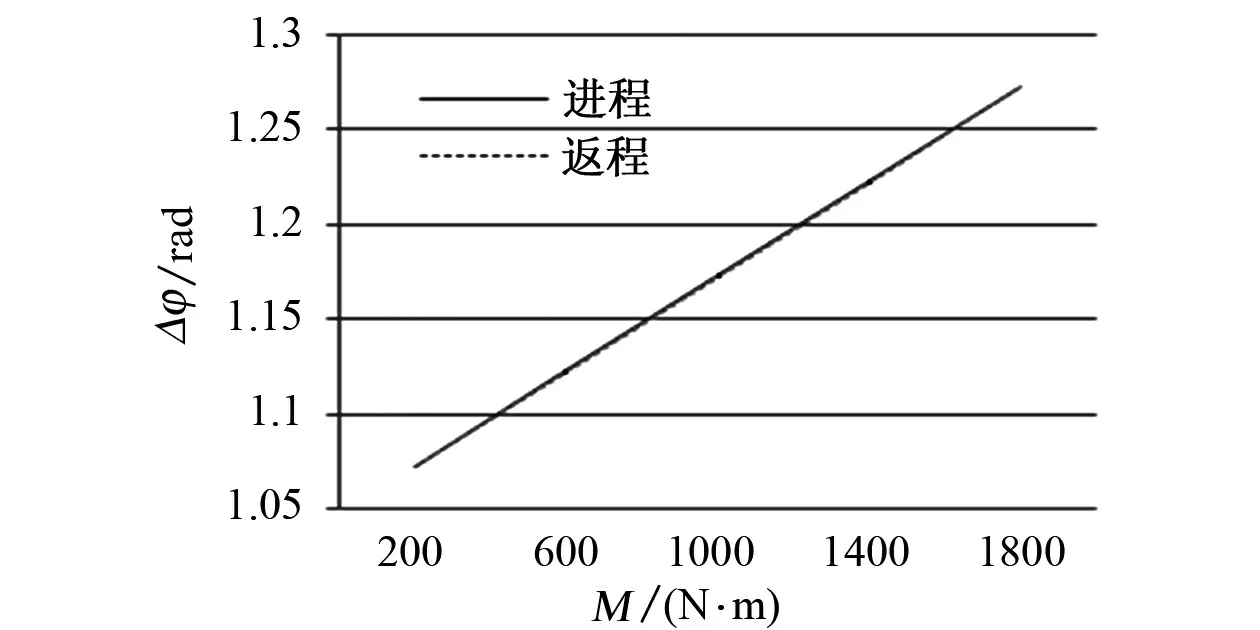
图10 扭矩重复性测试Fig.10 Repeatability tests of torque

5 结束语

本文详细介绍了基于光电相位偏差的转轴扭矩测量中的零位识别与处理方法，设计了整个测量系统和信号调理电路，并使用该测量方法及测量系统进行了相关实验，验证了本系统可以实现一些特殊场合下相位差零位信号的测量，提高基于相位差测量原理的转轴扭矩测量的便利性和测量精度，拓宽其应用场合。