风电机组串联系统维修方法的研究

谢鲁冰， 芮晓明， 林瑜茜， 霍明庆

(华北电力大学 能源动力与机械工程学院，北京 102206)

工业技术的发展在带来经济繁荣的同时，也引发了能源革命，清洁新能源的开发和利用迫在眉睫。风能作为一种可再生、绿色清洁能源越来越受到全世界的关注[1]。随着风电机组单机容量的不断增大，维修费用率的占比呈现逐渐上涨趋势[2]。风力发电机组变得越来越复杂，故障率随之提高，所以在追求风力发电的同时，必须考虑其可靠性和可维护性[3]。基于风力发电机可靠性分析的维护决策研究不仅在安全性方面至关重要，而且从经济效益的角度看也很重要。

多部件预防维修的原理大致可以分为3类：基于时间的计划型维修、基于状态的视情型维修和随机状态下的机会型维修[4]。

对于陆上风电机组，由于起步较早，运维已经趋于成熟化。Mathew等[5]针对风力机寿命监测系统的优化，通过基于状态维修与基于机会维修的优化策略相结合的方式，论证了优化策略的选择对于寿命监测系统准确性的有效作用；Baidya等[6]基于模糊层次分析法，构建了风电机组状态监测模型；Serrano-Gonzlez等[7]在研究风电机组市场化发展方式的过程中，也同样提出针对关键部件的预防性机会维修策略对于降低运维成本以及后续大型风电场的建设和融资可行性分析均具有借鉴意义。

对于海上风电机组，由于海上风能资源丰富，不受陆上风电弃风限电的影响，海上风电开发已经成为全球新能源开发的热点与前沿[8]。但海上风电开发难度大、建设成本高和技术不成熟等因素已成为限制海上风电发展的主要因素，同时海上恶劣多变的风浪条件、备品备件的管理优化和技术人员的资质水平等诸多因素均加剧了海上风电维修的困难性和复杂性。Sarker等[9]建立了基于海上风机组件的多层次机会维修费用率模型，采用机会更换、机会维修以及故障维修同时进行机会维修的方式来降低维护费用率；刘璐洁等[10]考虑到海上风电机组所处的特殊运行环境，针对其运行维护时的等待问题，提出了基于可靠性和维护优先级的预防性维护策略；Shafiee等[11]考虑海上备品备件的后勤管理，并结合海上风浪条件，提出了基于运行状态与预防性机会维修策略；Ambuehl等[12]以降低海上风电机组风险度和提高可利用度为目标，引入海上风电天气因素的灵敏度分析，提出了基于状态维修的优化策略。

上述研究提出了诸多关于风电机组预防维修的方法，但是在对风电机组进行实地考察后，发现具体实施过程中，存在一些不够完善的方面：(1)在选择维修方式时出现偏差，导致错过最佳维修时机；(2)维修过程中存在 “维修欠缺”和“维修过度”的现象；(3)维修过程系统将出现可用度偏小而维修费用率偏大的情况[13]。

针对以上问题，笔者以风电机组串联系统为研究对象，分别以维修费用率最小、可用度最大及综合考虑两方面因素建模，对风电机组的计划型和机会型预防维修方法进行对比研究。

1 模型建立

将双馈异步式风电机中齿轮箱和高速轴简化为一个串联系统。假设预防维修周期间隔变化，利用可靠度表征随机故障，同时保证串联系统存在可靠度下界，分以下3个部分来建模[14]：(1) 以风电机组串联系统维修费用率最小为目标进行建模；(2) 以风电机组串联系统可用度最大为目标进行建模；(3)综合考虑维修费用率最小、可用度最大进行建模。

2 计划型预防维修模型

计划型预防维修是指无论系统是否正常工作，基于系统的运行特性直接进行维修的行为。早期的计划型预防维修以周期性维修[15]为主，近年来随着维修理论的发展与完善，不完全维修[16-18]开始被引入实践。

以下分别建立基于维修费用率最小的计划型预防维修模型(C模型)、基于可用度最大的计划型预防维修模型(A模型)和综合考虑维修费用率最小、可用度最大的多目标预防维修模型(U模型)并进行计算分析。

2.1 C模型

2.1.1 模型建立

齿轮箱F1在进行第i次预防维修时出现故障问题的平均次数为初始故障率函数对预防维修周期长度的积分：

(1)

高速轴F2在进行第i次预防维修时出现故障问题的平均次数为故障率对预防维修周期长度的积分：

(2)

一个周期内维修费用率为：

(3)

齿轮箱F1在第i次预防维修周期结束时的可靠度为：

(4)

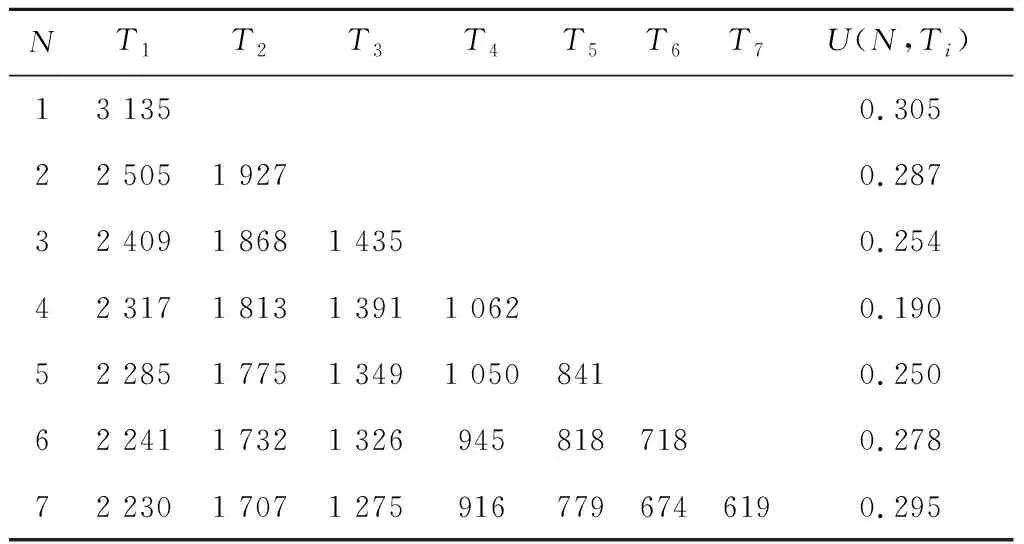
其中：0

串联系统维修费用率最小的计划型预防维修模型为：

(5)

(6)

式中：c1为对F1进行一次故障小修所需费用；c2为对F2进行一次故障维修所需费用；c3为对F2进行一次故障维修时，给F1带来的额外费用；c4为对F1进行一次计划预防维修所需费用；c5为对F1进行维修的同时对F2检修一次所需费用；t1为对F1进行一次故障小修时机组的停机时间；t2为对F2进行一次故障维修时系统停机时间；t3为对F2进行一次故障维修时，拆装F1花费的停机时间；t4为对F1进行一次计划预防维修时机组的停机时间；r(t)为F1的初始故障率函数；ω为F2的故障率；x为组件的役龄回退因子[19]，01；N为组件整个使用周期内参与维修的周期数；Ti为第i个预防维修周期的长度；Tk表示第k(1≤k≤i-1)个预防维修周期的长度；RL为F1正常工作时的可靠度下界。

2.1.2 分析求解

风电机组选型参考江苏中广核某风场[21]。齿轮箱F1的寿命为威布尔分布，其形状参数τ和尺度参数ζ分别为2.3和310，因此平均设计寿命为15a。高速轴F2的寿命为指数分布，因此故障率ω=4。其余参数可假设为：c1=3，c2=5，c3=3，c4=12，c5=7；t1=48，t2=72，t3=96，t4=192；x=0.35，y=1.1，RL=0.9。

计算结果如表1所示。由表1和图1可知，串联系统的维修次数N随维修方式的改变而变化。当N<5时，串联系统的维修费用率C随维修次数的增大而减小；当N=5时方程达到最小值，维修费用率为48.63元，此时串联系统最满意的计划型预防维修周期间隔为T1=2 146 h、T2=1 776 h、T3=1 387 h、T4=1 103 h、T5=895 h；当N>5时，维修费用率随维修次数的增大而增大。因此，当N=5时，可对风电机组相关部件进行预防性更换。当N=8、T8=543 h时，计划型预防维修周期间隔接近风场常规的计划检修周期，如果再继续增大N，系统停机过于频繁，会增大维修成本，因此为了不增加额外成本开销，不再增大N。

表1 C模型计算结果

图1 C模型优化结果

2.2 A模型

2.2.1 模型建立

建立系统可用度最大的计划型预防维修模型如下：

(7)

(8)

该模型适用于同时考虑可用度最大化和确保串联系统工作时可靠度下界正常的情况。

2.2.2 分析求解

利用Matlab进行数值模拟，得到表2结果。由表2和图2可知，当N<4时，系统可用度A随N的增大而增大；当N=4时，A达到最大值0.869，此时串联系统最满意的计划型预防维修周期为T1=2 499 h、T2=1 857 h、T3=1 399 h、T4=1 033 h。即当N=4后便可对系统进行相应部件的更换，这样可确保串联系统的可用度最大。相比C模型，A模型的N减小，但对部件的更换频率增加，因此采用A模型虽然可以保证系统处于较高的可用度，但是多次更换部件将增加维修成本。

表2 A模型计算结果

图2 A模型优化结果

2.3 U模型

为协调维修费用率和可用度之间的矛盾，建立一个以维修费用率最小、可用度最大为目标的可调节模型。

2.3.1 模型建立

综合考虑维修费用率最小、可用度最大的多目标方程为：

U(N,Ti)=C(N,Ti)-A(N,Ti)

(9)

统一量纲并引入权重系数ρ1和ρ2：

(10)

通过调节ρ1和ρ2的大小可以反映出不同可靠性指标的权重，ρ1+ρ2=1。

可调节的多目标预防维修模型为：

(11)

该模型同时考虑了计划型预防维修中的维修费用率和可用度，称之为U模型。

2.3.2 分析求解

当ρ1=0.5、ρ2=0.5时，Matlab计算结果如表3所示。由表3可知，当N<4时，模型计算结果随维修周期的增大而减小;当N=4时，达到最小值0.190，此时对应的风电机组齿轮箱的最满意预防维修周期为T1=2 317 h、T2=1 813 h、T3=1 391 h、T4=1 062 h，继续增加N，计算结果增大。

表3 U模型计算结果

ρ1=0.6、ρ2=0.4，ρ1=0.5、ρ2=0.5和ρ1=0.4、ρ2=0.6这3种情况下U随N的变化情况如图3所示。由图3可知，即使模型选取不同的权重系数，当N=4时，U(N,Ti)的计算结果都取得最小值。即在第4次计划型预防维修周期结束后对串联系统中的相应部件进行更换，不仅维修费用率小，同时还能保证系统可用度较高。

图3 不同权重下U模型的优化结果

将不同模型的最优解进行对比，结果见表4。

表4 不同模型计算结果的对比

由图4不同模型的优化结果可知：

(12)

图4 不同模型的优化结果

3 机会型预防维修模型

机会型维修是指维修系统中的某一部件时，同时维修或更换短时间内需要维修的其他部件。该方式将减少系统的预防维修总次数，从而缩短系统停机时间，达到降低机组维修成本的目的[22-23]。

以维修费用率最小为目标函数，建立机会型预防维修模型(OC模型)；以可用度最大为目标函数，建立可用度最大的模型(OA模型)；以维修费用率最小、可用度最大为双目标，建立可调节模型(OU模型)。将上述3种模型的计算结果与风电机组计划型预防维修模型的计算结果进行对比。

3.1 OC模型

3.1.1 模型建立

齿轮箱寿命l的分布函数为F(X)，密度函数为f(X)，高速轴寿命分布函数为G(X)，密度函数为g(X)。M时刻高速轴的寿命分布函数表示为：

(13)

密度函数为：

(14)

平均维修费用率为：

(15)

式中：c0为对齿轮箱进行一次机会维修消耗的费用；L1为串联系统在第1个预防维修周期内进行机会型维修的阈值；M为当齿轮箱的寿命超过L时，高速轴第一次出现故障的时刻。

对平均维修费用率的期望函数进行求导，分析其在(0,T1)区间内是否存在最小值点，该最小值点即最优机会维修阈值L*。

(16)

已知单周期平均维修费用的期望E[C(L)]在区间上是连续函数，因此当-c0+c2+c3+c4>0时，期望函数的导数可取得最小值。将导数方程的根代入进行比较，可以得到最优机会维修阈值L*，即为OC模型。

3.1.2 分析求解

由前文计算结果可知，风电机组齿轮箱最满意的计划型预防维修周期间隔为T1=2 146 h、T2=1 776 h、T3=1 387 h、T4=1 103 h、T5=895 h。

各计划型预防维修周期内的最优机会维修阈值见表5。

表5 OC模型各计划型预防维修周期内的最优机会维修阈值

第一个计划型预防维修周期T1内其他参数计算结果见表6。

表6 OC模型计算结果

由表6可知，风电机组齿轮箱在T1=2 146 h内的L*是1 155 h，换言之，对齿轮箱进行机会维修的最佳时间是运行1 155～2 146 h，此时维修时间虽然相较于原计划提前了，但是系统的维修费用率减少了22.74%。这与Sulabh的模拟结果一致。

3.2 OA模型

3.2.1 模型建立

系统可用度为：

(17)

平均维修费用率在区间(0,T1)2个端点处的导数为：

(18)

3.2.2 分析求解

基于可用度最大时的最满意计划型预防维修周期来确定最优机会预防维修策略。

由第2.2节的计算结果可知，风电机组齿轮箱最满意的预防维修周期间隔为T1=2 499 h、T2=1 857 h、T3=1 399 h、T4=1 033 h。通过计算可获得各计划型预防维修周期内的L*,如表7所示。

表7 OA模型各计划型预防维修周期内的最优机会维修阈值

第一个计划型预防维修周期T1内其他参数计算结果见表8。

表8 OA模型计算结果

由表8可知，风电机组齿轮箱在T1=2 499 h内的L*是1 388 h，即对齿轮箱进行机会维修的最佳时间是运行1 387～ 2 498 h之间，此时维修虽然在时间上相较于原计划提前了，但是系统的维修费用率减小了6.09%，符合Sulabh的模拟结果。

3.3 OU模型

3.3.1 模型建立

基于前文计算构造一个新的混合目标函数：

U(LU)=E[C(LU)]-E[A(LU)]

(19)

统一量纲并引入权重系数ρ1、ρ2：

(20)

该模型即为OU模型。

3.3.2 模型求解

由上文计算结果可知，风电机组齿轮箱在ρ1=0.5、ρ2=0.5，ρ1=0.6、ρ2=0.4和ρ1=0.4、ρ2=0.6这3种情况下最满意的T1分别是2 317 h、2 288 h和2 393 h。通过计算可得L*，如表9所示。

表9 OU模型最优机会维修阈值

选取不同权重系数ρ1、ρ2，得到不同权重系数下U模型的计算结果，如表10所示。

表10 OU模型计算结果

由表10可知，通过调整ρ1、ρ2的大小，风电机组齿轮箱在第1个计划型预防维修周期内，在表10所示的机会维修阈值时，对齿轮箱进行机会维修，均可使目标函数维修费用率减小，可用度增大。可见，风电机组在维修过程中可多考虑OU模型的机会型预防维修。

无论ρ1、ρ2的数值如何变动，始终满足如下关系式：

(21)

这表明风电机组串联系统的计划维修中，如果着重于减小维修费用率，综合模型更接近OC模型；如果追求系统可用度大时，综合模型更接近OA模型。

4 结 论

(1)在风电机组串联系统的计划型预防维修模型的研究中，以串联系统的维修费用率最小为目标函数，得出最满意的计划型预防维修周期间隔为T1=2 146 h、T2=1 776 h、T3=1 387 h、T4=1 103 h、T5=895 h；以系统的可用度最大为目标函数，得出系统最满意的计划型预防维修周期为T1=2 499 h、T2=1 857 h、T3=1 399 h、T4=1 033 h；综合考虑两方面因素构建了多目标的计划型预防维修模型，如果维修费用率方面分配的权重更大，则综合模型更接近基于维修费用率最小模型，如果可用度方面分配权重更大，则综合模型更接近基于可用度最大模型。

(2)与计划型预防维修模型的计算结果进行比较，发现采用机会型维修决策后，系统在单周期内的维修费用率节省了22.74%，可用度提高了6.10%。因此，机会型维修决策可以进一步减小单周期内系统的维修费用率，并提高系统可用度。