调谐质量阻尼器对漂浮式风力机稳定性的影响

2018-08-29 02:21黄致谦郝文星

动力工程学报 2018年8期

黄致谦，郝文星，李春，2，叶舟

(1.上海理工大学能源与动力工程学院，上海 200093； 2.上海市动力工程多相流动与传热重点实验室，上海 200093)

随着陆上风电场可开发资源的减少，海上风能因能量密度高、湍流度低等优势逐渐被世界各国重视，“由陆地向海洋”也已成为未来风电场发展的必然趋势[1-2]。目前，海上风电场主要集中在浅水区域，对于风资源更丰富、风况更优的深水区域，使用漂浮式风力机更加经济。与陆上风力机不同，海上风力机在运行过程中始终承受波浪载荷作用，因此其载荷特性更加复杂。与固定式风力机相比，漂浮式风力机底部基础不固定，其始终处于不平衡受力、非定常运动状态，此非线性载荷不仅会影响机舱内传动系统的正常工作，也会降低风力机的发电效率，甚至可能发生塔架屈曲、倾覆等事故[3-5]。与传统海工平台相比，漂浮式风力机平台重心位置更高、水线面更小，波浪载荷加剧了平台的运动，剧烈的运动甚至会导致平台倾覆。因此，探究如何保障漂浮式风力机在复杂多变的海洋环境中安全稳定地运行具有重要意义。

目前，国内外学者针对漂浮式风力机的稳定性展开了诸多研究。文献[6]中提出将螺旋侧板应用于漂浮式风力机Spar平台的结构设计中，并采用势-黏结合的方法研究螺旋侧板对Spar平台动态响应的影响。针对漂浮式风力机对风载荷和波浪载荷响应过大的问题，文献[7]中提出共用系泊的大型漂浮式风电场概念，并基于水动力软件Aqwa研究其运动响应特性，发现共用系泊可明显提高平台稳定性。以上研究的不足之处在于将叶片、塔架和平台等结构简化为刚体，风载荷简化为轴向推力，这种简化无法精确描述非定常气动载荷，更无法揭示在风、波浪载荷下塔架、叶片等结构的变形、屈曲等非线性动态响应过程。部分学者通过控制叶片变桨和电机变扭矩来降低叶片气动载荷，进而提高漂浮式风力机的稳定性。Namik等[8]研究了独立变桨对平台运动的控制效果。Fischer等[9]提出一种基于加速度反馈的非线性控制方法，在理论上分析漂浮式风力机的稳定性。以上研究虽然在一定程度上提高了漂浮式风力机的稳定性，但会加剧叶片根部的疲劳载荷。

调谐减振装置作为结构控制技术被广泛应用于高耸柔性结构设计中，实验和数值计算表明其对于高楼、电视塔等高耸柔性结构具有明显的减振效果[10]。调谐减振阻尼器主要包括调谐质量阻尼器(TMD)和调谐液体阻尼器(TLD)。文献[11]中将TMD应用于海上风力机塔架中，并采用有限元方法研究其对风力机塔架振动的减振效果。Stewart等[12]、Lackner等[13]和Sethuraman等[14]研究了TMD对漂浮式风力机稳定性的影响，但未考虑外载荷作用，仅为自由振动分析。关于提高漂浮式风力机稳定性的研究虽在TMD结构控制方面取得了诸多成果，但均做了适当简化。

因此，笔者采用在机舱配置TMD的控制方法，研究其对海上漂浮式风力机塔顶位移和平台摇荡特性稳定性的控制效果，以期为海上漂浮式风力机的稳定性控制提供一定的理论参考。

1 研究对象

研究对象为基于ITI Barge平台的NREL 5 MW风力机，其参数如表1所示[15]，平台参数如表2所示[16]。漂浮式风力机模型如图1所示。

表1 NREL 5 MW风力机参数

表2 ITI Barge平台参数

图1 漂浮式风力机和Barge平台示意图

Fig.1 Schematic diagram of the floating wind turbine and Barge platform

2 研究方法

利用基于NREL开发的气动弹性结构动力学仿真软件FAST研究TMD对漂浮式风力机结构动力学响应的影响。FAST软件中考虑气动-水动-结构-控制耦合并基于时间推进方法实现对非线性运动方程的求解[17-18]。在气动模块中，考虑轴向及切向风诱导影响的情况下基于Pitt-Peters动态入流理论求解风轮平台诱导速度;基于叶素-动量理论，在考虑叶尖损失及轮毂损失的情况下求解风轮气动力，并采用Beddoes-Leishman动态失速模型进行修正。利用水动模块计算漂浮式风力机平台的水动力载荷，包括水线面的面积惯性矩和浮力；漂浮式风力机平台属于大尺度结构物，可采用辐射/绕射理论求解波浪力；系泊系统采用悬链线模型。在弹性模块中，结合Kane方法和模态法，在考虑子结构刚柔特性的条件下建立风力机多体动力学模型，其中叶片、塔架和低速传动轴为具有分布质量、刚度和模态等属性的柔性体模型，将轮毂、高速传动轴和机舱等视为刚性体模型。以气动模块求解所得气动力和水动模块求解所得水动力作为输入载荷，得到该时间步长下的结构动力学响应，并反馈至控制模块、水动模块和气动模块，控制模块会根据结构模块的反馈信息进行相应的控制，如变桨控制、偏航控制和TMD控制等。仿真流程如图2所示。

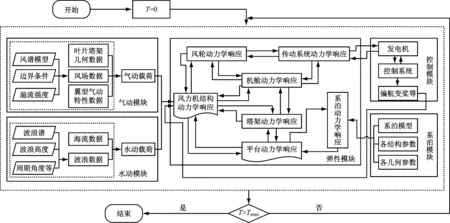
图2 仿真流程

3 TMD及其动力控制方程

TMD由质量系统、弹簧系统、阻尼系统和支撑系统组成，TMD通过改变自身质量或刚度来达到调整自振频率的目的，使其接近被减振结构的固有频率或外部载荷频率。当被减振结构在外部载荷下产生振动时，会带动TMD振动，TMD产生的调谐惯性力反作用于被减振结构，并通过阻尼系统将能量耗散，以达到结构稳定性控制的目的。将TMD布置在机舱内部，如图3所示。

图3 机舱布置TMD示意图

4 湍流风场及不规则波浪建模

4.1 风场模型建立

为模拟时历高风速湍流风作用下漂浮式风力机的结构动力学响应特性，需建立随时间和空间变化的湍流风模型。常见的风场建模方法分别为基于测风塔的实测数据，即通过模糊逻辑预测、神经网络预测等方法得到一定空间范围内的风速分布，适用于小空间风场建模；基于大涡模拟方法(LES)，即在考虑大气边界层效应等条件下实现风场建模，所需计算资源极大；基于风电场实测数据，即通过气象分析方法获得风场风速数据，适用于小尺度空间风场建模。鉴于此，笔者基于Kaimal风谱并考虑空间相干性建立了三维时历风场模型。

根据风力机的几何参数，设定风场覆盖区域尺寸(水平和垂直方向)为195 m×195 m。由于漂浮式平台有6个自由度，导致叶片存在垂荡和横荡运动，为保障三维风场始终完全覆盖叶片，故风场布置较大，风场区域远超过风轮的扫略区域。设定网格节点为15×15，如图4所示。考虑空间相干性，通过Kaimal风谱获得每一节点的风速分布，通过空间相干模型获得整个风场的风速分布。空间相干模型如下:

(1)

式中：Si,j(f)为节点i、j的互功率谱；C(Δr,f)为空间相干大小；Δr为节点间距离；Si,i(f)和Sj,j(f)分别为节点i、j的功率谱。

图4 风场计算区域及网格

以轮毂中心为参考点，以时历平均风速11.4 m/s为参考风速，仿真时间为600 s，建立三维时历湍流风风场，轮毂高度处三维风速分布如图5所示。轮毂点时历风速分布如图6所示。由图6可知，湍流风在u方向的风速波动范围为10.52～12.55 m/s，v方向的风速波动范围为-1.052 0～0.993 2 m/s，w方向的风速波动范围为-0.637 8～0.664 8 m/s。

图5 轮毂高度处的风速分布

4.2 波浪谱及不规则波浪建模

波浪谱以风和波浪为参量，通过定义有义波高、波浪周期和有限风区等参数，即可得到波浪的大致形式。波浪谱是随机波浪的重要统计信息，可直接给出波能相对频率和方向的分布。国内外学者研究海洋结构时对波浪载荷几乎均采用波浪谱方法[19-23]。目前，常见的波浪谱有P-M谱、Jonswap

(a) u方向风速分布

(b) v方向风速分布

谱和布氏谱等[24]。其中，可由大西洋波浪统计数据分析得出P-M谱，其适合描述充分发展的波浪[25]，可表示为

(2)

式中：Sζ(ω)为功率谱；U为某参考高度处的平均风速；g为重力加速度；ω为波浪圆频率。

选取P-M波浪谱生成的有义波高为5 m，波浪谱峰周期为12.4 s，基于设定参数建立不规则波浪场，如图7所示。

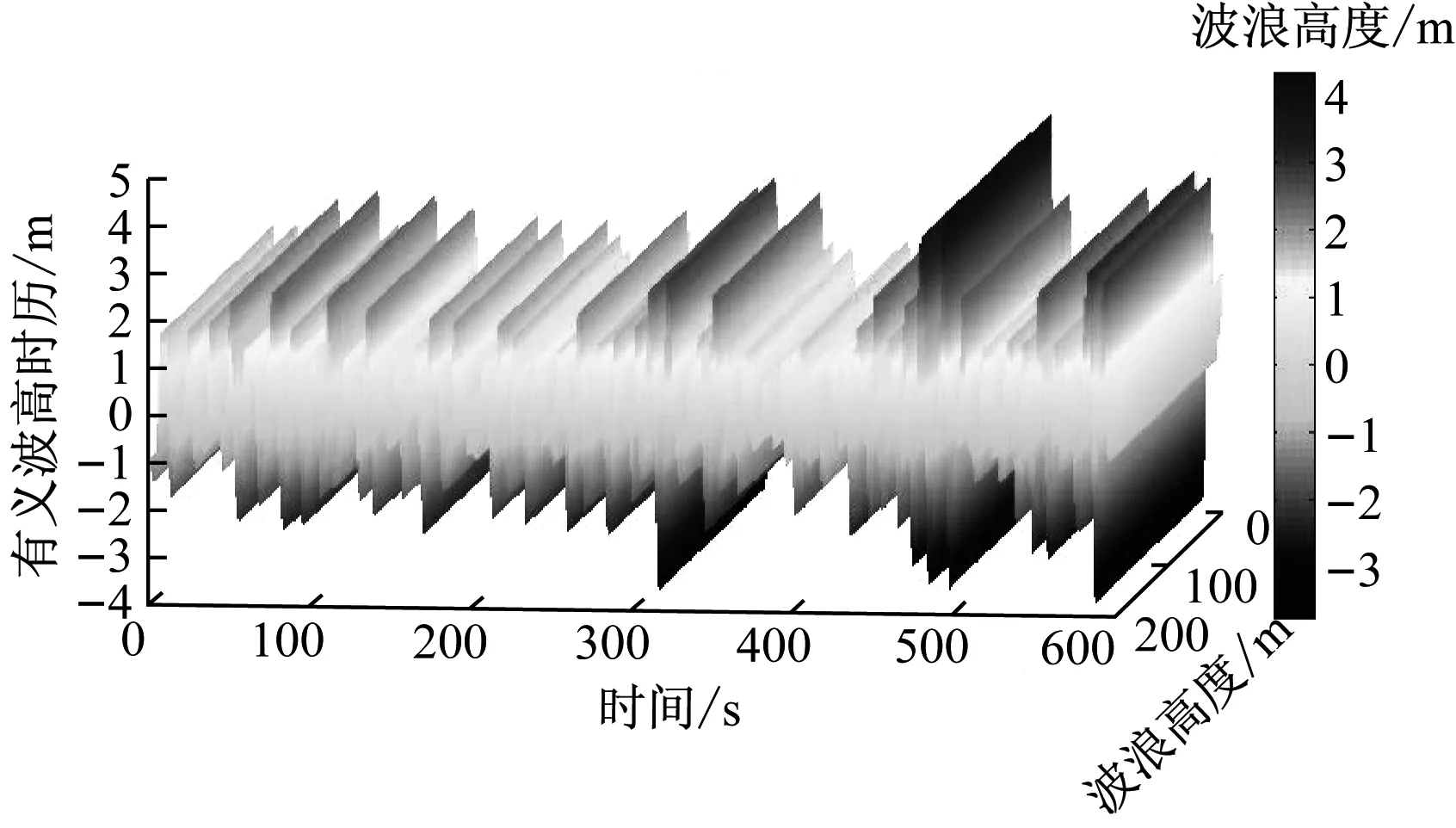
图7 不规则波浪模型

5 TMD对漂浮式风力机稳定性的影响

在风载荷和波浪载荷作用下,漂浮式风力机的稳定性主要表现为塔顶位移特性和平台的摇荡特性。塔顶位移过大会引起风轮叶片在旋转过程中不稳定，诱发塔架大幅振动并导致失稳，而平台摇荡特性与漂浮式风力机整机结构的强度及疲劳载荷有关，对风力机的安全性有很大影响。故笔者主要研究在风、波浪载荷作用下TMD对漂浮式风力机塔架塔顶位移和平台摇荡特性的影响。

5.1 TMD对平台摇荡特性的影响

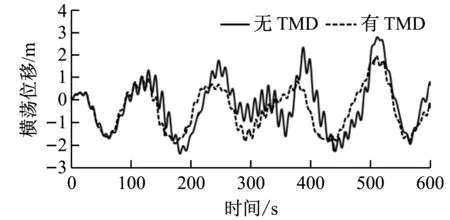
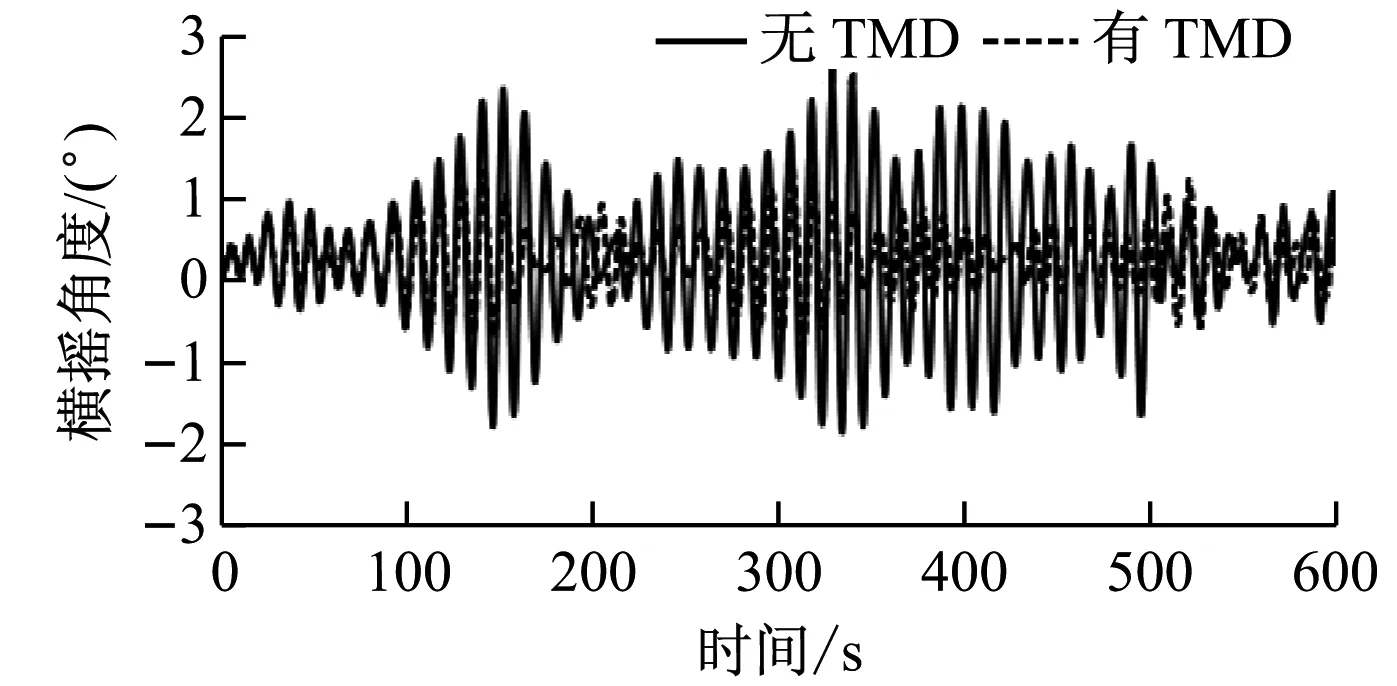
漂浮式风力机在TMD控制下平台摇荡特性的时历曲线如图8所示，横坐标为时间，纵坐标为平台各自由度的运动响应。

(a) 纵荡

(b) 横荡

(d) 横摇

(e) 纵摇

(f) 首摇

由图8可知，加入TMD控制后，平台的纵荡位移、垂荡位移和纵摇角度变化较小，而横荡位移、横摇角度和首摇角度变化较为明显。在TMD控制下，平台的最大横荡位移由2.78 m减小至1.96 m，降低了29%，横荡位移波动范围由-2.35～2.78 m减小至-1.92～1.96 m；横摇最大角度由2.38°减小至1.32°，降低了45%，横摇角度波动范围由-2°～2.38°减小至-1°～1.32°，减幅明显；首摇角度的变化规律不明显。有、无TMD控制时平台横荡位移标准差分别为0.851和1.034，在TMD控制下稳定性提高了18%；有、无TMD控制时平台横摇角度标准差分别为0.541和0.917，在TMD控制下稳定性提高了41%。由于平台纵荡、垂荡和纵摇的变化不明显，且首摇变化规律不明显，故仅给出横荡与横摇的幅值谱，如图9所示。

由图9可知，平台横荡和横摇的频谱峰值对应的频率分别为0.01 Hz和0.09 Hz;加入TMD控制后平台的横荡幅值从0.23减小至0.14，降低了39%；加入TMD控制后横摇幅值从0.19减小至0.12，降低了36%，减幅均较明显，说明TMD控制对平台横荡和横摇的控制效果显著。

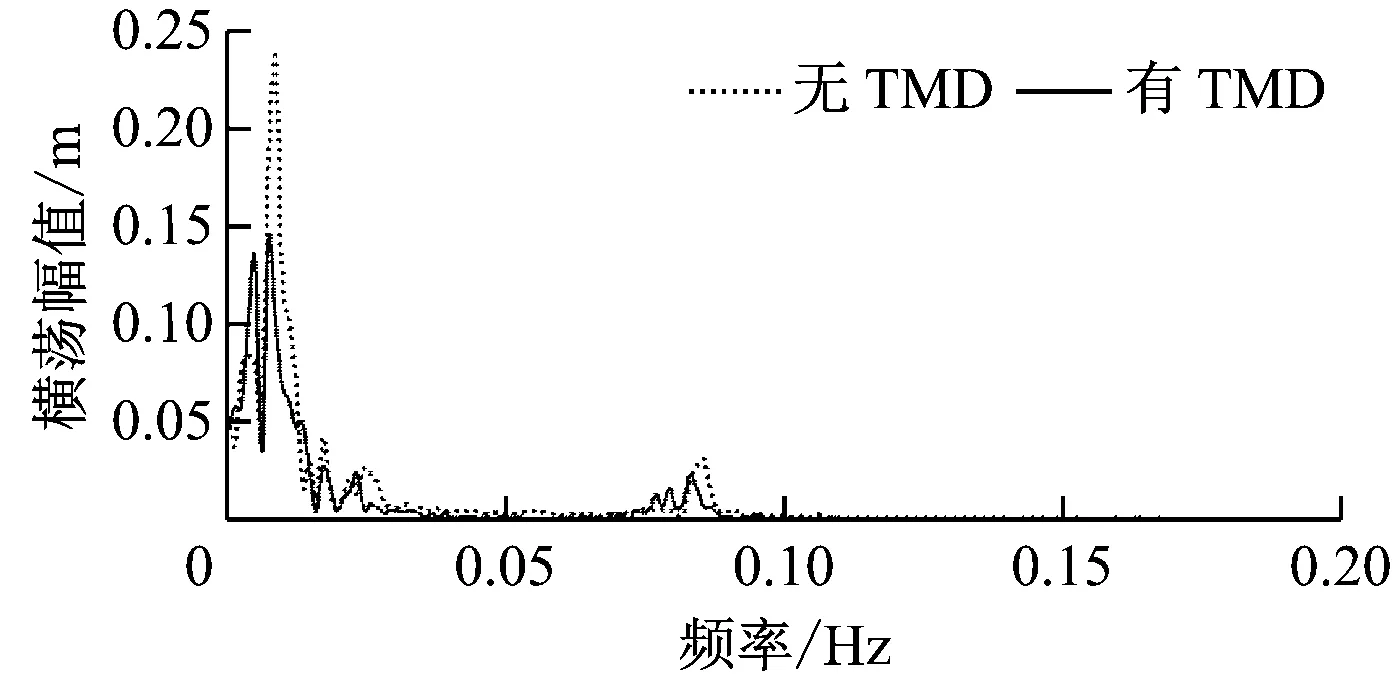
(a) 横荡

(b) 横摇

5.2 TMD对塔顶位移的影响

漂浮式风力机在TMD控制下的塔顶位移时历曲线如图10所示。由图10可知，漂浮式风力机在无TMD控制情况下，开机前塔顶前后位移在-1～1 m内较为规律地波动；在开机(大约70 s)后，塔顶侧向位移以约150 s的周期运动。在TMD控制下，塔顶前后位移基本不变。在无TMD控制下，塔顶侧向位移在-0.09～0.06 m之间波动，在TMD控制下仅在-0.06～0.02 m之间波动，侧向位移明显减小，其最大值降低了66%。在有、无TMD控制下塔顶侧向位移的标准差分别为0.030和0.048，即有TMD控制后塔顶侧向位移标准差降低了38%。塔顶位移幅频特性曲线如图11所示。塔顶前后及侧向位移的频谱峰值分别在0.06 Hz和0.08 Hz附近。无TMD控制时塔顶前后及侧向位移幅值均大于有TMD控制时的幅值，但塔顶前后位移幅值变化较小，而侧向位移幅值减小明显。