基于Mann-Kendall的汾河水库年径流量 变化研究*
(山西省水利水电科学研究院,山西 太原 030002)
山西省是一个水资源严重短缺的省份,全省人均水资源占有量仅有381m3,位居全国排名倒数第二,更远远低于国际公认的严重缺水界限,水资源的短缺严重制约着山西省国民经济发展和人民生活水平提高。另外,受气候影响,降水分布极不均匀,是山洪灾害频发的省份之一,旱情经常发生。本文选用非参数Mann-Kendall[1-3]检验方法,分析了汾河水库1960—2016年共57年的年径流量变化,研究了汾河水库年径流量的分布特征及其变化趋势,对于深入了解该地区水资源的特征和未来水资源的演变趋势具有一定的现实意义。
1 研究区概况
汾河水库是山西省内的一座大(2)型水利枢纽工程,水库的主要任务是防洪、灌溉、城市与工业供水,兼顾发电、旅游、养殖等综合效益。汾河水库防洪标准为:设计洪水为100年一遇,校核洪水为2000年一遇。汾河水库还担负着下游太原、晋中、临汾、运城四个城市所辖的18个工农业县市区以及沿途铁路干线、省际高速和太原附近的煤矿、化工、钢铁、电力等大型厂矿企业的防洪任务;承担着太原市生态供水,太原一电厂、太钢、古交等工业供水,汾河灌区149.55万亩农田灌溉用水。
汾河水库1960—2016年的年径流量见表1。
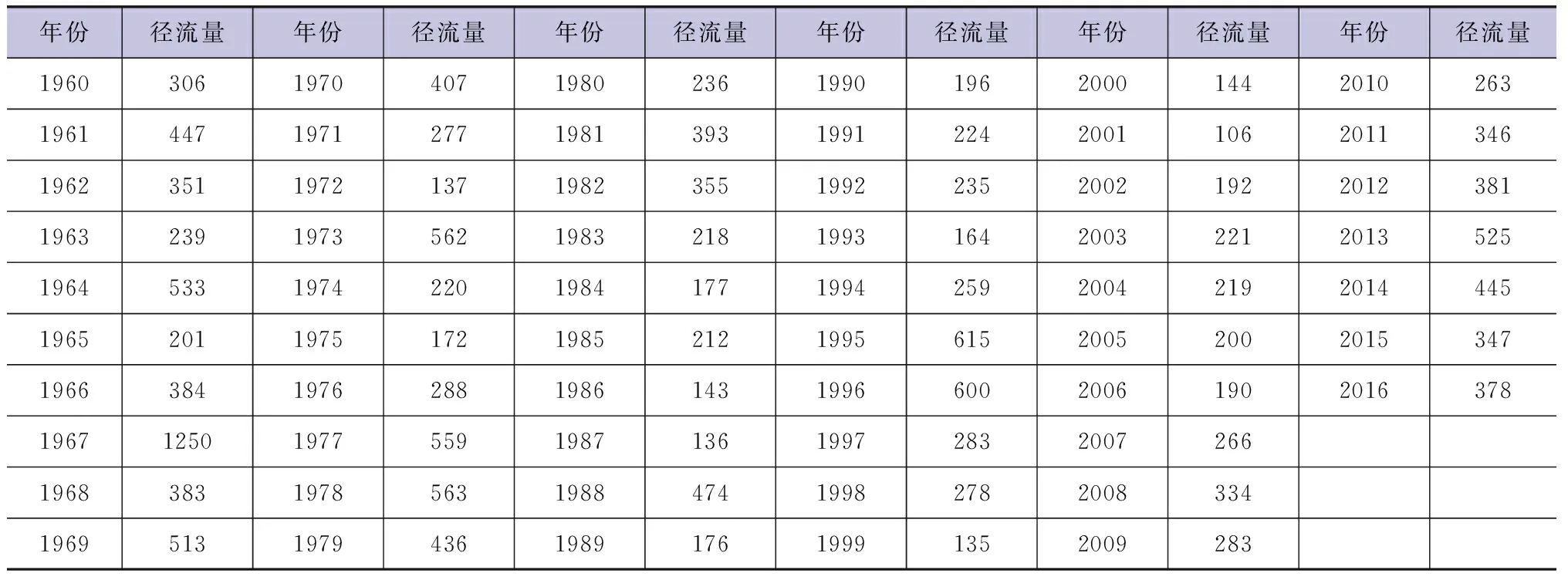
表1 汾河水库1960—2016年年径流量 单位:100万m3
2 研究方法
选用非参数Mann-Kendall[1,4]统计趋势检验法来检验山西省汾河水库年径流量的长期变化趋势。Mann-Kendall趋势检验广泛应用于连续时间序列的趋势分析,实际中常用于判定某一时间序列趋势的显著性,也可进行时间序列突变点检验。M-K检验法(非参数秩次相关检验)中,统计量的计算是其核心,可用来判定序列趋势是否显著。M-K检验法属于非参数检验方法(亦称无分布检验),与传统的参数检验方法比较,其优点是不需要时间序列样本服从特定的分布,也不受序列中少数异常值的干扰,计算比较简便,因此在实际中被广泛应用。
假设水文时间序列为Xt(t=1,2,…),其对偶数S的计算公式为
(1)
其中:
S——序列所有对偶观测值Xi,Xj(i 再根据S值确定以下参数: M=τ/στ (2) (3) (4) 式中N——序列长度; M——kendal秩相关检验系数; τ、σ——计算M的因子。 取α=0.05的显著水平,则统计量UF和UB的临界值为±1.96。如果M>Mα/2则时间序列有明显的趋势;若计算所得M值为正,则表明时间序列具有上升或递增的趋势,反之则表示序列具有下降或递减的趋势。 本研究中,N=57,由公式(1)~(4),可得:στ2=0.0083,σ=0.09,S=724,τ= -0.09,M= -1,|M|<1.96. 结果表明:1960—2016年山西省汾河水库年径流量总体呈下降趋势。 为更好地分析汾河水库年径流量的下降趋势,假定时间序列随机独立,定义统计量: (5) 式中,UF1=0,E(SN)和var(SN)是累计数SN的均值和方差: (6) (7) 计算所得的UFN组成一条曲线UF,用相同的方法应用到反序列中,通过计算得到UBN,组成另一条曲线UB。若UF和UB曲线在临界线内变动,表明时间序列变化趋势和突变不明显,若UF或UB值<0,则时间序列呈下降趋势;UF或UB值>0,则序列呈上升趋势;超过临界线,则上升或下降显著,若UF和UB线在临界线出现交点,则交点对应的时刻便是时间序列突变开始的时间,若交点在临界线外,则可结合其他检验方法来明确判定该点是否为突变发生时刻。 具体UFN、UBN计算结果见表2及右图。 表2 E(SN)、var(SN)、UFN、UBN计算结果 1960—2016年汾河水库年径流量M-K突变检验曲线 从上图中的M-K突变检验曲线可以看出,UF曲线和UB曲线有三处交点,说明汾河水库年径流量的突变点发生在1964年、1967年和1970年;从右图中还可看出,从1980年开始,UF值<0,说明汾河水库年径流量从1980年开始呈现总体下降的趋势。 本文运用Mann-Kendall 非参数检验方法对山西省汾河水库年径流量进行趋势和突变检验分析,得到以下结论:近57年来,汾河水库年径流量总体上呈减少趋势,并在1964年、1967年、1970年有突变现象。根据本文研究所得汾河水库年径流量的变化特征,可为汾河水库流域的水资源管理、水库防洪调度等提供一定的科学参考。3 结果分析

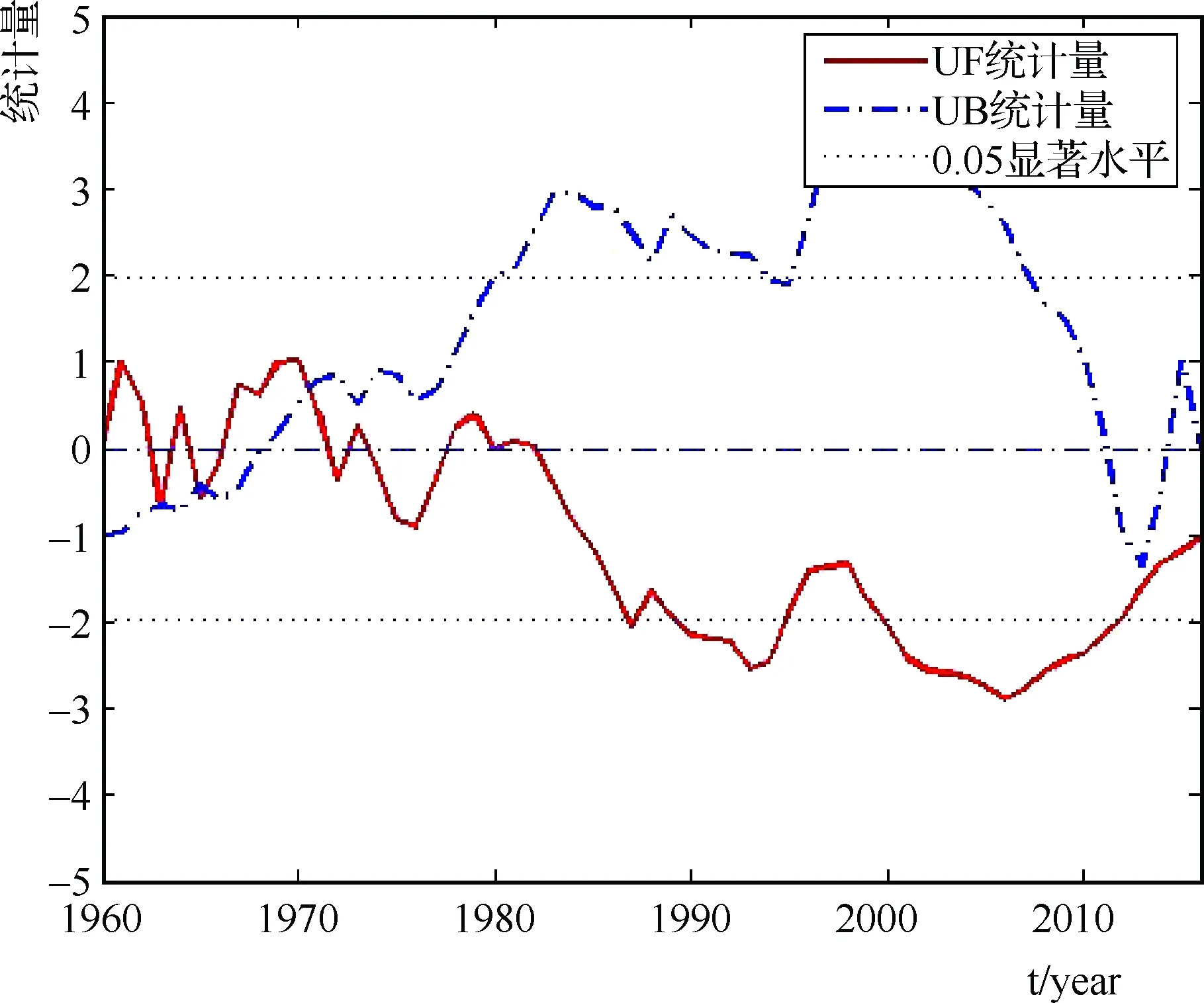
4 结 语

