高邮灌区“集水期灌”稻田水平衡模型 及期灌制度改进

李坤霖，孙 勇，卫 琦,2，季婧钰，徐俊增,2

(1.河海大学水利水电学院，江苏 南京 210098; 2.河海大学水文水资源与水利工程科学国家重点实验室，江苏 南京 210098; 3.江苏省高邮市水利局，江苏 高邮 225600)

0 引 言

灌溉制度是编制和执行灌区用水计划的重要依据，而借助水量平衡模型模拟土壤水分动态是制定合理灌溉方案的主要手段。目前国内外相关学者关于稻田水量平衡模型的构建、灌溉模型的优化以及灌溉制度制定已开展了大量的工作[1-3]。孙景生等[4, 5]运用水量平衡方程确定了旱作物的灌溉制度。Hatfield[6-8]等人为获得高额稳定的单位面积产量,并控制土壤湿度，配合相应的农业管理技术,使作物产量达到最高，以此制定灌溉制度；李青[9-15]等通过对比分析多种灌溉制度在不同水文年的应用，提出了不同作物的节水、增产灌溉制度。Kuo[16-21]等国内外专家学者通过CROPWAT、ISAREG、Aquacrop 等模型，在保证作物正常生长的条件下，模拟了不同的灌水方案，并对灌区灌溉制度提出优化建议。而关于通过调整作物不同阶段的灌水延续时间以达到节水灌溉效果的研究还比较少。

“集水期灌”制度是指在灌溉用水管理过程中, 采取“集约调水、生理配水、定时供水、制度节水”的灌溉制度和用水管理模式[22]。高邮灌区自2001年起开始实行“集水期灌”制度以来，灌水周期采取泡田栽插期4 d左右、分蘖期5 d、晒田以后6 d左右，简称“456”灌溉制度。多年来，该灌溉制度仍存在着灌水次数多、灌溉定额大、灌溉水利用系数不高等问题，在灌水资源越发严峻的背景下，优化灌溉制度、提高灌溉水利用效率对于解决农业用水危机具有重要的理论意义。因此，针对传统“456”灌溉制度存在的不足，本研究拟对灌水间隔进行调整，提出“467”灌溉制度(灌水周期采取泡田栽插期4 d左右、分蘖期6 d、晒田以后7 d左右)，并借助率定后的水量平衡模型对两种灌溉制度的效果进行分析比较，其研究结果对于高邮灌区“集水期灌”灌溉制度的改进调整具有重要的指导意义和应用价值。

1 数据与方法

1.1 试验区概况

试验区位于江苏省高邮市卸甲镇周庄村(119°11′E，32°35′N)境内，属北亚热带季风气候区，年平均气温14.6 ℃，常年降雨量1 037 mm，多年平均蒸发量1 060 mm。无霜期242 d，最高气温38.5 ℃，最低气温-18.5 ℃，相对湿度75%左右，寒暑显著，易旱易涝。受海洋季风的影响，6-9月份降雨偏多，多年平均汛期降雨量占多年平均雨量的59.5%。浅层地下水位埋深0.5～1.2 m，土壤耕层质地为黏壤土，适宜水稻、小麦、棉花、油菜等多种粮经作物生长。

根据高邮市1955-2014年的降水资料，将所有年份的降雨量按从大到小进行排序，依次得到n=1、2、3、4、5.....的降雨量，将上述排列的各数值换算为对应频率的降雨量，计算公式为：p=n/(i+1)，i为总共的统计年份，在频率纸上将上述各值回归，连成平顺曲线，用内插法在曲线上查出对应25%、50%、75%及95%频率时的降雨量值，确定了1974、1986、1999和1978年分别为丰水年、平水年、枯水年和特枯年。

1.2 稻田水平衡模型

稻田水平衡方程为：

hi=hi-1+Pi+Ii-Di-Si-ETi

(1)

式中:hi为第i天的田间水层深度，mm；hi-1为第i-1天的田间水层深度，mm；Pi为第i天的降雨量，mm；Ii为第i天的灌溉量，mm；Di为第i天的排水量，mm；Si为第i天的渗漏量，mm；ETi为第i天的腾发量，mm。

1.2.1 水稻需水量计算

水稻采用常规灌溉，其蒸发蒸腾量计算公式为：

ETi=KsiKciET0i

(2)

式中：ETi为第i天的耗水量，mm；Ksi为第i天的土壤水分胁迫修正系数；Kci为第i天的作物系数。其中参考作物蒸发蒸腾量根据FAO-56推荐的Penman-Monteith公式来计算。式中所需的气象资料来源于中国气象科学数据共享服务网。Kci采用单作物系数法确定，其中水稻生育阶段按照初始期、发展期、中期和末期4个阶段划分，生育天数分别为20、25、45、30 d。Ksi应用以下的数学模型，在逐日作物需水量预测中计算土壤水分胁迫修正系数：

(3)

式中：θi-1为第i-1日实际土壤含水率, 对于水稻, 以占饱和含水率百分数计;θc为土壤水分胁迫临界含水率百分数，水稻为80%；ε为经验系数，取0.95。

1.2.2 渗漏量

根据稻田有无水层2种情况，分别计算其渗漏量：

(1)若田间有水层，渗漏量可按照与水层深度之间的线性关系进行计算，其公式为：

Si=ahi+b

(4)

式中：Si为第i天的渗漏量，mm；hi为稻田水层深度，mm；a、b为拟合参数。

(2)若田间出现无水层，在稻田土壤含水率高于田间持水率时仍会有少量的渗漏，此时稻田渗漏可按下式计[23]：

(5)

式中：Si为第i天自由排水通量，mm；K0为饱和水力传导度，主要与土壤质地有关，土壤愈黏重，其值愈小，一般取0.1～1.0 m/d；α为经验常数，一般为50～250，土壤愈黏重，其值愈大；ti为土壤含水率从饱和状态达到第i天水平所经历的天数；H为水稻主根层深度，m。

1.2.3 降雨容蓄

当一次降雨不超过田面允许水深上限时，其降雨量均为有效降雨量；当降雨量超过大于田面允许的最大水深时，其超过部分为排水量，其公式为：

(6)

式中：Re为一次降雨的有效降雨量，mm；R为一次降雨量，mm；H0为一次降雨开始时田面水层深度，mm；Hmax为田面允许最大蓄水深度，mm。

1.3 参数率定

基于2010年田间A和B田块的实测土壤水分与水层数据为率定样本，借助水量平衡模型对作物系数Kci、饱和水力传导度K0、拟合参数a和b以及经验常数α等变量进行率定，以实测水层深度和模拟水层深度之间的误差平方和最小为目标，利用最小二乘法进行求解。以田块C为验证样本对参数率定结果进行验证。模型效率主要取决于Nash-Sutucliffe模型有效系数R2，R2越接近于1表明模型效率越高，同时ME也是衡量模型效率的重要指标，其值越接近于0表明模型模拟效果越好。为使模型效率较高，即需要目标函数最小。

1.4 改进与比较

在现行“集水期灌”456灌溉制度的基础上对灌水间隔进行调整，提出“467”灌溉制度。并通过率定的模型推求“456”和“467”灌溉制度，分析和对比两种灌溉制度的差异及灌水后的水分特征和降雨利用率等效果，其中降雨的有效利用率采用下式计算：

ρ=∑R0/∑R

(7)

式中：ρ为降雨利用率；其余符号意义同上。

2 结果与讨论

2.1 田间水量平衡模型的率定与验证

由最小二乘法计算得到的水稻作物系数Kc值取Kc1=1.006，Kc2=1.400，Kc3=0.910；渗漏量模型参数分别取a=0.15，b=1.00，K0=0.35，α=175.03。

通过对田块水层深度的模拟数学统计，率定样本误差平均值分别为4.23和2.28；绝对值误差平均值同样相对较低，分别为9.08和5.50。比较其相关系数发现，各田块实际观测值与模拟值的相关系数较高，均达到0.85以上。由图1(a)可见各典型田块水层深度模拟值与实测水层深度值吻合较好，模型参数设置合理，模型可靠。

在水量平衡原理的基础上，利用率定参数计算验证样本的田间水位，通过研究可以发现，率定模型模拟的验证样本的田间水位也能较好的反应田间实际水位情况[如图1(b)所示]。

2.2 基于水平衡模型的集水期灌灌溉制度改进

采用率定模型推求了高邮灌区不同典型降水年的“456”和“467”两种灌溉制度，其灌水次数、灌水量和灌溉定额如图2和表1所示。

图1 基于模型模拟的田间水层与实测值对比情况Fig.1 Comparison of field water layer and measured value based on model simulation

图2 不同降水年下两种灌溉制度的灌水量比Fig.2 Comparison of irrigation volume under two irrigation systems among annual rainfall levels

由图2可以看出，不同典型降水年型下“456”灌溉制度的灌水次数和灌水定额分别为11～14次和4 000～5 000 m3/hm2，而“467”灌溉制度的灌水次数和灌水定额范围则分别为9～12次和3 300～4 305 m3/hm2。其中，1978年(特枯年)灌水次数减少了2次，灌溉定额相比较减少14.1%；1999年(枯水年)灌水次数减少了2次，灌溉定额相比较减少10.7%；1986年(平水年)灌水次数减少了2次，灌溉定额相比较减少15.7%；1974年(丰水年)灌水次数减少了2次，灌溉定额相比较减少17.6%。总体上，与传统“456”灌溉制度相比，不同典型降水年下的“467”灌溉制度均能有效减少灌水次数及灌溉定额，在节约灌溉用水的同时，节省了时间和经济成本。

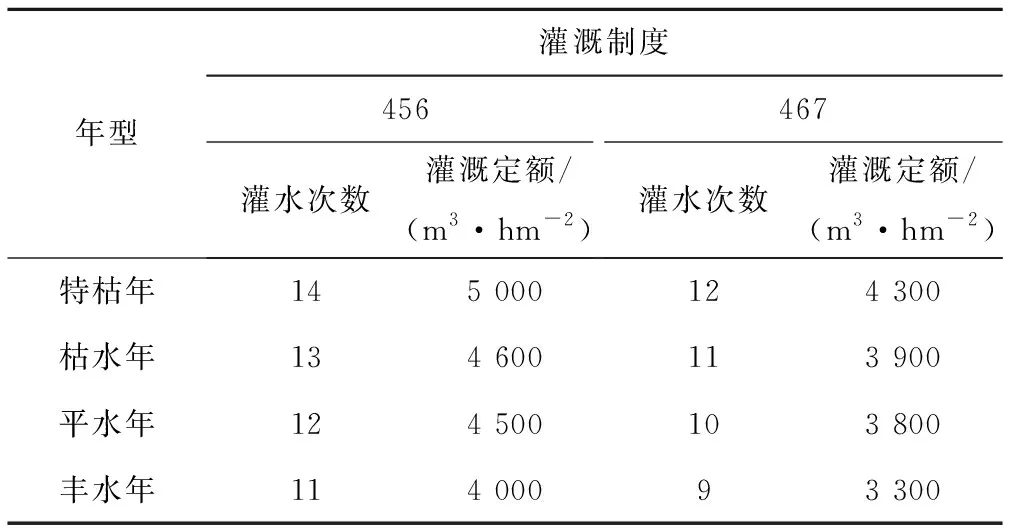
表1 不同降水年型下两种灌溉制度灌水次数、灌溉定额比较Tab.1 Comparison of irrigation times and quota of two irrigation systems among annual rainfall levels

注：“456”灌溉制度是指灌水周期采取泡田栽插期4 d、分蘖期5 d、晒田以后6 d，“467”灌溉制度是指泡田栽插期4 d、分蘖期6 d、晒田以后7 d。

2.3 不同灌溉制度下田间水分动态

不同降水年型下两种灌溉制度的土壤水层和含水率变化如图3所示。可以看出，与“456”灌溉制度相比，“467”灌溉制度下的土壤水层和含水率均较为相似。其中在土壤水层方面，“456”灌溉制度在1978(特枯年)、1999(枯水年)、1986(平水年)和1974(丰水年)年的平均水层深度分别为2.27、3.49、3.04 和3.77 cm，而“467”灌溉制度的平均水层深度为1.96、3.30、2.91和3.32 cm。而在土壤含水率方面，“456”灌溉制度在各降水年型黄熟期前的土壤相对含水率范围分别为68.9%～100%、76.9%～100%、92.6%～100%和94.2%～100%；“467”灌溉制度的含水率范围则分别为67.7～100%、68.1%～100%、85.7%～100%和94.2%～100%。1978(特枯年)采用“456”的灌溉制度，在分蘖期的土壤含水率最低达到86.7%，高于规范的灌水下限60%，在拔节孕穗-乳熟期，田间长期保持有水层，土壤含水率最低为72.7%，均高于各时期的灌水下限；1978年采用“467”的灌溉制度，在分蘖末期的土壤含水率最低达到85.3%，高于规范的灌水下限60%，在拔节孕穗期-黄熟期，田间呈现干湿交替的状态，土壤含水率最低为67.7%，各生育阶段含水率均高于灌水下限。1999(枯水年)采用“456”的灌溉制度，在分蘖期的土壤含水率最低达到86.8%，高于规范的灌水下限60%，在拔节孕穗-乳熟期，田间长期保持有水层，土壤含水率最低为78.9%，均高于各时期的灌水下限；1999年采用“467”的灌溉制度，在分蘖末期的土壤含水率最低达到82.0%，高于规范的灌水下限60%，在拔节孕穗期-黄熟期，田间长期保持有水层，土壤含水率最低为75.4%，均高于各时期的灌水下限。1986(平水年)采用“456”的灌溉制度，在分蘖期田间基本保持有水层，其余时期的土壤含水率最低为92.6%，高于各时间段的灌水下限；1986年采用“467”的灌溉制度，在拔节孕穗期以前田面均保持有水层，拔节孕穗期最小土壤含水率为85.7%，抽穗开花期最小土壤含水率为86.5%，乳熟期的最小土壤含水率为91.8%，均高于各阶段的灌水下限。1974(丰水年)采用“456”的灌溉制度，在分蘖-抽穗开花期田间长期保持有水层，乳熟期最小土壤含水率为98.1%，高于灌水下限；1974年采用“467”的灌溉制度，在分蘖-抽穗开花期田间长期保持有水层，乳熟期最小土壤含水率为94.3%，高于灌水下限。两种灌溉制度下的土壤水分差异并不显著 (p>0.1)。由此可以看出，与“456”灌溉制度相比，“467”灌溉制度较好地保证了灌溉后的土壤水分特征，使土壤水层和含水率范围均维持在水稻适宜生长的范围内。

2.4 不同灌溉制度下降雨利用率的比较

不同灌溉制度下的降雨利用率如表2所示，可以看出，不同水平年下“456”灌溉制度的降雨利用率范围为86.2%～100%，而“467”灌溉制度下的降雨利用率则增加了1.2%～6.5%。这主要是由于在不同年型降雨量均确定的前提下，“467”灌溉制度下的排水量较“456”灌溉制度的值减小了7.2～23.8 mm，因此，其降雨利用率有所增加。可见，“467”灌溉制度的降雨利用率总体上高于“456”灌溉制度下的值，且其在特枯年的降雨利用率最高，达到100%，其余降水年型降雨利用率较为接近。

表2 不同降水年型下不同灌溉制度的降雨利用率比较Tab.2 Comparison of rainfall utilization rate of different irrigation systems among annual rainfall levels

注：“456”是指灌水周期采取泡田栽插期4 d、分蘖期5 d、晒田以后6 d，“467”是指泡田栽插期4 d、分蘖期6 d、晒田以后7 d。

3 结 论

基于田间实测土壤水分与水层数据，借助水量平衡模型对作物系数进行了率定，并利用率定模型推求了不同典型降水年下“集水期灌”稻田的“456”和“467”灌溉制度。通过对比分析两种灌溉制度的效果，可以得出：与传统“456”灌溉制度相比，不同降水年下的“467”灌溉制度均有效减少了灌水次数和灌溉定额，提高了降雨利用率，在实现节水的同时，保证了土壤水层和含水率均维持在作物适宜生长的范围内。

图3 不同降水年型下不同灌溉制度土壤水分变化规律Fig.3 Variations of soil moisture of different irrigation regimes among annual rainfall levels

□