Matlab在数字信号处理中的应用

陈 赫，吕丽君

（长治学院 电子信息与物理系，山西 长治 046011）

1 引言

文章研究的Matlab在数字信号处理中的应用建立在数字滤波器的基础上，因为数字滤波器是信号处理中一种常见的设备。准确来说，数字滤波器搭载了能够过滤时间离散信号的数字系统，这样技术人员可以通过应用数学理论处理取样数据的方式，来实现对处理范围内数字信号的处理。

2 Matlab和数字信号处理概述

数字信号处理指的是通过计算机或者是专门的数字信号处理设备，应用专门的数字数值计算理论和方法，对数字信号进行转换、过滤、识别、评估、更改、运算等操作，以此令抽象的数值具备实际应用价值，为数字及数字信号的应用奠定基础。数字信号处理也开始成为通信专业、电子专业、计算机专业的主修课程之一。由于数字信号处理具有较强的专业性，学习内容涉及到了大量的学术理论、计算过程、演算分析方式等，这需要学习者和研究者具备一定的逻辑思维能力和运算能力，并且要适当掌握计算机编程[1]。

Matlab是美国的Mathworks公司新推出的一款计算型软件，该软件具备了数据分析、数值计算等多种功能。除了主体系统外，Matlab还包括了搭载了多种功能的工具箱，这些工具箱能够解决使用者在数字信号处理过程中遇到的各种问题，此外，工具箱中还包含了大量由数学专家编制的函数公式，这些函数公式都可以被直接应用在数字信号处理中，进而简化了数字信号处理的编程。

3 Matlab在数字信号处理中的应用方式

3.1 双线性法设计IIR数字滤波器

从理论上来讲，数字滤波器实际上是一个离散的运算系统，可用于对数字滤波器的进一步分析。以双线性法设计形式展示出来的数字滤波器所对应的单位脉冲样值有无限个，这种能够保持无限单位脉冲样值的数字滤波器便被称为无限脉冲响应数字滤波器，简称IIR数字滤波器，这便是本节要探讨的数字滤波器[2]。

IIR数字滤波器的设计流程较为简单，可以概括为探索滤波器各个系数，并使其无限接近设计目标和设计要求。Matlab引导下的IIR数字滤波器的设计方式有两种：一种是直接设计方式，也可以称为最优化设计方式的选择，先由设计人员确定一种最优化设计方案，并在其中明确指出误差最小确定准则和误差最大确定准则，随后再在此设计方案的基础上计算滤波器系数；一种是间接设计方式，先由设计人员设计一个符合数值信号处理要求的模拟数字滤波器，然后再将具体的数字信号处理要求和技术条件应用到模拟数字滤波器中，最终设计出符合数字信号处理要求的数字滤波器。

现以参照butter函数设计的butterworth数字滤波器为例，分析应用Matlab间接设计IIR数字滤波器的方式。

首先，应用butter函数设计butterworth数字滤波器，需要调用以下格式：[b,a]（其中a和b分别代表数字滤波器的变量）=butter（N,Wn），此格式被应用在低通型数字滤波器和常通型数字滤波器设计中；[b,a]=butter（N,Wn^,high^）,此格式被应用在高通型数字滤波器设计中；[b,a]=butter（N,Wn^,stop^）,此格式被应用在阻挠型数字滤波器设计中；[b,a]=butter（N,Wn^,S^）,此格式被应用在模拟数字滤波器设计中[3]。

其次，参照阶数N到截止频率Wn的计算公式，可以计算出butterworth数字滤波器中的分子和分母的多项式系数，并以Wn为计算标量，将计算范围控制在0-1之间，且使其逐一对应抽样计算频率的一半。

最后，以IIR数字滤波器的设计指标为参考依据，将数字滤波器的阻带截止频率控制在0.3 pi，并确保其最小衰减不超过15 dB。

双线性法设计IIR数字滤波器的特性曲线如图1所示。

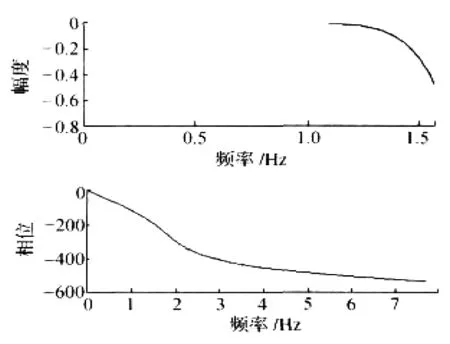
3.2 窗函数设计FIR数字滤波器

3.2.1 窗函数设计FIR数字滤波器的方式

FIR数字滤波器的脉冲响应时间是有限制的，基于此原理，应用窗函数来设计FIR数字滤波器。设计人员需要先计算出符合设计要求的数字滤波器的频率响应机制，以此来逼近最优的FIR数字滤波器设计方式，但是此时的设计工作需要在规定的时域内完成，此时通过傅里叶反变导数可以推导出窗函数设计公式。

但由于FIR数字滤波器应用的是无限长序列，并且这些设计序列之间不存在显著的因果关系，因此，设计人员需要在设计过程中应用有限长序列来逼近无限长序列，并且用窗函数序列来截取无限长序列，最后再通过Matlab软件来检测设计结果和精确程度，并检测模拟数字滤波器的性能是否符合FIR数字滤波器的设计要求[4]。

窗函数设计FIR数字滤波器的基本思想是根据给定的滤波器技术指标，选择滤波器长度N和窗函数w（n）,使其具有最窄的主瓣和最小的旁瓣。其核心是由给定的频率特性通过加窗确定有限长单位脉冲响应h（n）。考虑到数字滤波器的频率响应是以2π为周期的周期函数,若指标所要求的频响为Hd（ejw），则与它相应的序列Hd（n），根据DTFT变换对的关系有：

3.2.2 应用Matlab工具箱设计FIR数字滤波器的方式

现以Matlab工具箱为例，分析FIR数字滤波器的设计方式，并应用窗函数来检验FIR数字滤波器设计的标准程度。

第一，建立矩形窗，调用格式W=boxcar（n）,此时根据长度（n）可以产生一个矩形窗W；第二，建立三角窗，调用格式W=triang（n）,此时根据长度（n）可以产生一个三角窗W；第三，建立汉宁窗，调用格式W=hanning（n）,此时根据长度（n）可以产生一个汉宁窗W。

4 结束语

相对于其他类型的数字信号处理软件来说，Matlab能够更加精确的确定线性相位系统，进而节约了大量的编程时间，并且大幅度的提高了编程效率和速度，并且设计人员修改编程也较为方便，随着该软件版本的不断更新，其运行系统和数据运算功能也在逐渐完善。