应对枢纽失效的轴辐式网络枢纽备份

胡晶晶，黄有方

(上海海事大学经济管理学院，上海201306)

(*通信作者电子邮箱yhuang@shmtu.edu.cn)

0 引言

轴辐式网络物流系统中，轴辐式网络枢纽点存在失效风险，失效后的恢复策略包括枢纽设施和通道的重新修复和备份。维护轴辐式网络的正常运转需要考虑投入成本及一些不确定因素，如:翁克瑞［1］研究带固定轴线成本的轴辐式网络，强调合并运输的固定轴线成本，用拉格朗日算法求解;Yang等［2］考虑金融和服务的不确定性，提出了一种模糊双目标轴辐式网络设计问题，用两阶段法求解;Yang等［3］针对交通成本和时间的混合不确定性，提出了综合的轴辐式网络规划和优化问题。有学者考虑轴辐式网络中枢纽失效的风险进行网络结构可靠性研究，如:Zhalechian等［4］在运营和破坏风险的基础上设计一个具有弹性的轴辐式枢纽网络，考虑了三个主要的弹性维度，包括主动能力、反应能力和设计质量;An等［5］针对枢纽和反应中断管理的失败可能会给轴辐式网络带来恢复成本的问题，提出了可靠的轴辐式网络设计模型，在此模型中考虑了备用中心和备选路线的选择，以主动地处理枢纽中断问题。

轴辐式网络中的失效和恢复主要研究枢纽功能的变化失效和备份策略。Mohammadi等［6］建立混合随机规划模型研究不确定情况下轴辐式网络中持续的枢纽点位置的确定，并使用蚁群算法对大规模的实际数据进行计算验证;杨珺等［7］提出了考虑延迟惩罚并面向整个轴辐式网络的节点完全中断问题，建立节点中断的上、下界模型;刘舒佶［8］提出轴辐式网络枢纽功能性中断问题和模型，并通过数据测试比较遗传算法和禁忌搜索算法的优劣;Mohammadi等［9］考虑了枢纽的全部或者部分失效，设计基于枢纽位置问题的可靠轴辐式物流网络。以上文献的作者研究整个轴辐式网络的可靠性，但没有重点突出枢纽失效的应对方式。

进行精确计算的数学求解器和遗传算法在求解轴辐式网络问题方面都有所应用。Azizi等［10］研究轴辐式网络枢纽失效的影响，分别采用数学求解器CPLEX和遗传算法求解，比较分析了单个备份枢纽和多个备份枢纽策略。Kratica等［11］使用两段编码法和适当的目标函数，运用两种遗传算法进化方法研究美国货运航空轴辐式网络。王雅琪等［12］利用遗传算法研究非线性规模经济效应下轴辐式网络枢纽选址问题。轴辐式网络研究用到的方法还有博弈论，Sasaki等［13］竞争环境下的斯塔伯格模型轴辐式网络枢纽选址，设计了大型多枢纽轴辐式交通网络。将轴辐式网络的研究和车辆调度相结合，吕婷等［14］建立了轴辐式网络下的车辆调度模型，设计了基于启发式调度规则的节约算法进行求解。魏素豪等［15］构建了基于单分配、多枢纽、混合式网络结构特征的轴辐式公共交通网络优化模型，用模拟退火算法求解。

本文从提高轴辐式物流网络的安全稳定性角度，针对轴辐辐式网络中枢纽失效可能阻断正常的货流，预先为每个枢纽选择备份枢纽点，研究经过备份枢纽后流量的流经路线和流量大小的变化，求解不同成本权重下，初始轴辐式网络成本和备份枢纽构建成本的变化及对轴辐式网络结构的影响。

1 问题描述

初始轴辐式网络中纽点若失效转化为节点，其余枢纽点负荷增大，需要新的枢纽点来替代原枢纽点。并非枢纽失效之后才进行备份枢纽点的选择，而是给正常的枢纽点选择备份枢纽点。问题研究每个枢纽点的备份枢纽点的选择，分析影响备份枢纽的因素，不同备份枢纽的选择对总成本的影响，由备份枢纽和辐节点构成新的轴辐式网络的合理性。目标函数包括失效前的网络构建成本和应对失效的备份成本，并赋予权重α。分析目标函数中两部分投入成本的重要性占比权重α设置对轴辐式网络结构的影响。

2 数学模型

由于整个数学规划的约束较多，将应对枢纽失效的枢纽备份模型分成两部分阐述，分别是初始轴辐式网络基本模型和枢纽备份扩展模型。

2.1 初始轴辐式网络基本模型

初始轴辐式网络构建基本模型设计有两个决策变量，决定枢纽选址的0/1变量xij和表示经过枢纽点的货物OD(Origin to Destination)流的yikl，变量和参数设置如表1所示。当货流的起始点与目的点同属于一个枢纽点时，不考虑枢纽点之间的规模运输。

目标函数f1权重为α，如式(1)所示，总成本包括有四个部分，分别为:枢纽点的建设成本(式(2));货物由起始点运到枢纽点过程中的收集成本(式(3));由枢纽点运至目的节点的配送成本(式(4));干线运输成本(式(5));式(6)为节点分配关系约束，表示每一个节点只能作为枢纽节点或是枢纽点的辐节点，不能独立存在;式(7)表示只有当xkk为1时，即选择节点k作为枢纽节点，才能够将其他节点分配至节点k，否则节点k不能拥有辐节点;式(8)为节点i的货物流量平衡约束;式(9)为辅助约束，用以确保模型在节点距离不严格符合三角行不等式时仍然可以使用;式(10)、(11)为约束变量属性。

表1 初始轴辐式网络变量和参数Tab.1 Variables and parameters of initial hub and spoke network

2.2 枢纽备份扩展模型

枢纽备份扩展模型引入了新的变量和约束，用以表达枢纽备份思想，在原有的枢纽之间选择合适的备份枢纽，目标函数求枢纽备份成本。这部分模型是非线性的。

1)目标函数。当轴辐式网络由备份枢纽点重新构成时，新的成本产生且区别于正常情况下的成本，这部分成本的权重为1－α。式(12)目标函数f2由三部分构成。式(13)表示节点i经过原枢纽点k的货物由备份枢纽b替代，距离参数也从节点i到k变为节点i到b，计算在选择了备份枢纽b后的收集成本。式(14)表示经过备份枢纽b的分配成本。式(15)表示干线之间的流量运输由枢纽k的备份枢纽l进行，这一部分计算的是选择一个备份枢纽后的干线运输成本。因为在f1中已经计算了枢纽选址时产生的枢纽建设成本，备份枢纽是在已有的枢纽中选择的，因此不重复计算枢纽建设成本。这一部分的成本f2主要计算备份枢纽构建的新的轴辐式网络的物流成本，是资源投入用于防范枢纽失效后轴辐式网络失效的备份成本。

2)变量和约束。表2为扩展模型的新增变量的设置。式(16)、(17)表示当一个点是枢纽点时才可以被选为备份枢纽，研究的备份枢纽选择策略是从已有的枢纽中选择备份枢纽，当然，备份枢纽也可以从节点中选择，可以使原来的节点升级为枢纽点再选为备份枢纽，这里只从枢纽点中选择备份枢纽。式(18)表示每个枢纽点都有一个备份枢纽点，单个枢纽失效单个枢纽备份。式(19)表示当枢纽点k选为枢纽点a的备份枢纽点时，原来经过枢纽a和枢纽l之间的流量重新经过枢纽k和枢纽l。

表2 扩展模型变量Tab.2 Variables of extended model

3)非线性部分的线性化。模型中的计算涉及到原枢纽点和备份枢纽点，具有一定的复杂性，数学规划是非线性的，用变量替代的方法进行线性化。在式(20)、(21)中，把xik·zkb原来的枢纽选址决策变量xik和备份枢纽选择变量zkb的乘积用变量 hikb表示，hikb=xik·zkb，hikb≥ xik+zkb－ 1，其中 hikb=1表示节点i分配给枢纽点k，且枢纽点b选为枢纽点k的备用枢纽点。在式(22)至(24)中，zak·yial用变量viakl表示，并给出了线性化的变量代换过程。整数viakl=zak·yakl，viakl≥yial+(zak－1)M，viakl表示由节点i到枢纽点a的流量重新经过枢纽点k和备份枢纽l。用变量代换的方法增加了模型中的变量，将目标函数中的非线性乘积关系转化成有实际意义的具体变量，使非线性规划转化为线性规划。

扩展模型如下:

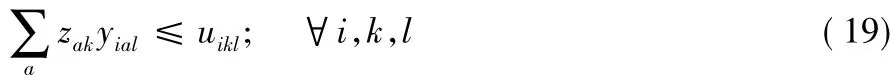
线性化如下:

总成本F式(25)由f1和f2构成，并分别赋予权重:

备份是为了预防枢纽失效或中断风险导致的轴辐式网络的失效。备份枢纽也会产生一定成本，合理的备份枢纽的设置可以和正常情况下的轴辐式网络成本进行平衡使总成本最低。

3 实验算例与分析

模型分别使用数学求解器CPLEX和遗传算法求解:

1)将扩展模型非线性部分线性化，线性化后和轴辐式网络初始模型一起构成了该问题的混合整数线性规划;Matlab调用CPLEX求解这个混合整数线性规划模型。

2)原模型遗传算法求解。

3.1 模型线性化之后的 CPLEX求解

1)轴辐式网络基本参数和权重敏感性分析。

CPLEX计算规模为16个设施点，目标函数F中成本f1赋予的权重为α，备份枢纽选择成本f2的权重为1－α。设置基本参数Cc、Cd、Ct，α为A、B、C、D四组不同的值依次如表3，对于每一组基本参数，设置权重 α 的变化取值为(0.1，0.3，0.5，0.7，0.9)。由于轴辐式网络结构还受到流量影响，在算例中固定流量矩阵wij。如表3，每一组枢纽点都会得到相同数量的备用枢纽点，备用枢纽点从原枢纽点中选择。有些枢纽点是重复选为备用枢纽点的。权重α的值依次递增，初始成本f1、枢纽备份下的成本f2和总成本F都在改变。随着权重的增加，枢纽点的数量在减少。因为权重的增加使f1所占的总成本的比例增加，f1的值是不断升高的，枢纽的选址在初始轴辐式网络中计算得到，因此当原轴辐式网络的成本f1增大时，枢纽的数量会不断减少以使总成本得到优化。

如图1选取B、C参数绘制纵坐标成本f1、f2，F随横坐标权重α的变化趋势。由图1可知，原枢纽成本f1增加，备份成本f2减少，总成本F先增加，后有小幅降低但仍高于起始点;α决定了f1、f2在成本投入所占的比重。备份成本主要由备份枢纽点构成的轴辐式网络成本。不同的轴辐式网络结构下选择备份枢纽后网络结构变化的复杂程度也是不一样的。图2中分别给出了不同参数设置下8个枢纽点、6个枢纽点、4个枢纽点的备份策略和轴辐式网络结构的改变。备份枢纽点一旦选定，它和辐节点的关系也重新得到了调整。设置的枢纽点较多时，有较少的辐节点需要被重新分配到备用枢纽点;当设置的枢纽点个数较少时，备份枢纽点更易于选取。

在图2(a) 中，第1、2、7、8、14 这五个枢纽点相距较近，第10、11、12这三个枢纽距离较近，它们选择备份枢纽也是在各自的聚集区域内选择。如1的备份枢纽是14，2的备份枢纽是8，7的备份枢纽是1，8的备份枢纽是2。

2)枢纽点容量敏感性分析。

考虑枢纽容量对备份枢纽影响时的目标函数和枢纽容量设置如下:

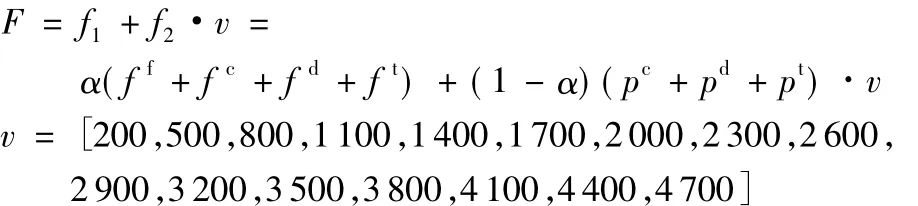
1)中基本参数和权重敏感性分析中分析了不同的收集成本、分配成本和转运成本系数以及权重对枢纽分配和备用枢纽选择的影响，保持1)中基本参数不变，进一步观察枢纽容量是否影响备份枢纽的选择，在目标函数中加入参数枢纽容量v，算例结果显示枢纽容量也会影响到轴辐式网络结构，改变枢纽容量的大小对轴辐式网络结构和备份枢纽点的选择也有一定的影响。为了降低节点间距离对枢纽选址的影响，体现枢纽容量参数的敏感性，改变坐标系，使各个节点的分布更加均匀。

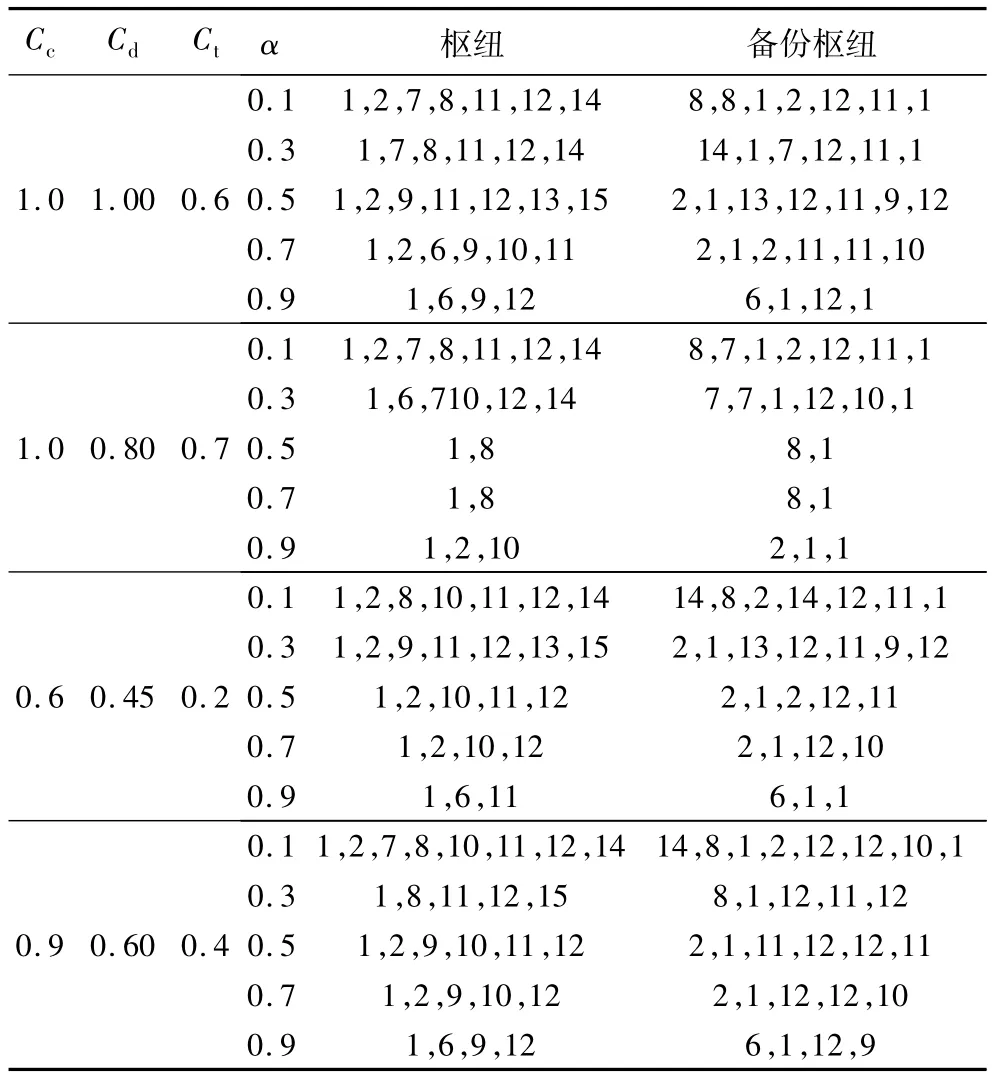
表3 不同参数下备份枢纽的选择Tab.3 Selection of backup hubs under different parameters

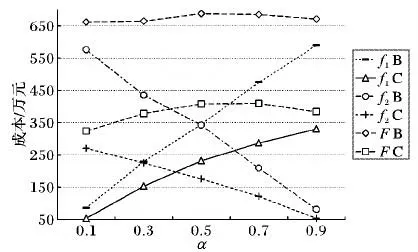
图1 B、C两组参数下成本f1、f2、F随权重α的变化Fig.1 Change of cost f1，f2and F with the weight of α under two groups of parameters of B and C

如表4所示，保持权重 α 为 0.1不变，Cc=0.1、Cd=0.7、Ct=0.6分别比较无容量限制和枢纽容量为v时的枢纽选址和备用枢纽选择策略，加入枢纽容量限制后，枢纽个数明显减少，同时备份枢纽也发生了变化。

在应急情况下，若是枢纽的容量足够大，枢纽间的转运相似于枢纽之间的备份选择策略，网络结构也不需要作较大的调整。

图2 不同参数设置下的备份枢纽选择Fig.2 Backup hub selection under different parameter settings

表4 枢纽容量对备份枢纽的影响Tab.4 Influence of hub capacity on backup hubs

3.2 枢纽备份遗传算法求解

1)算法设计。

轴辐式网络枢纽备份为非线性问题，利用遗传算法计算大规模轴辐式网络的枢纽选址和备份，体现了遗传算法全局优化、计算效率高的优势。使用枢纽选址数据集(http://people.brunel.ac.uk/～ mastjjb/jeb/info.html)用 Matlab 遗传算法工具箱求解。遗传算法基本设置:种群规模20;染色体基因数200;交叉概率0.7;变异概率0.4;执行代数200。有两个主要决策变量:轴辐式网络的枢纽点和相应的备份枢纽点。编码为0、1，给出一组染色体为枢纽选址的初始解。解码为1的点为枢纽点，在对备份枢纽的操作中，重新分配所有的原枢纽节点给备份枢纽点。

适应度函数根据目标函数α(ff+fc+fd+ft)+(1－α)(pc+pd+pt)进行评估，计算中令不变的固定成本ff为零。目标函数求解最小总成本，在设计适应度函数时综合考虑枢纽选址和备份枢纽选址对总成本的影响，调整α值观察变化。

在遗传操作中，选择操作采用轮盘赌法，选择距离最近的节点。交叉方法为单点交叉如图3。变异方法为单点变异，交换枢纽点基因位置。

图3 单点交叉Fig.3 Single point cross

2)遗传算法结果。

Matlab绘制遗传算法进化过程如图4所示，α为0.5，枢纽点个数为16，停止迭代时最大适应度值和平均适应度值变化不大、趋于稳定，适应度值中最优值收敛于1.26609E+08，平均值收敛于1.28755E+08。由图4(d)得到初始枢纽选址图形，初始枢纽对应的备份枢纽也计算得出，如表5所示。

图4 遗传算法进化过程Fig.4 Evolutionary process of genetic algorithm

遗传算法得到的轴辐式网络枢纽点和对应的备份枢纽点及成本变化情况如表5所示。

遗传算法计算规模为200个点，实验中6、9、16个枢纽选址和枢纽备份求解时间均低于CPLEX的计算时间。随着α值增加，虽然f2在总成本的比例变小，f1比例增大，由于f1中的固定成本ff设置为零，f1增加的速率小于f2减小的速率，所以当f2减少时，总成本减少。同时，选址的枢纽位置之间也越来越远。综上，适应度函数中枢纽备份成本f2对总成本F和枢纽点位置的影响是敏感的。

4 结语

本文建立混合整数非线性规划模型，探讨轴辐式网络枢纽备份策略，分别用遗传算法求解原模型，用CPLEX求解线性化的模型，得出了轴辐式网络枢纽备份问题的优化解，并分析影响轴辐式网络枢纽选址和枢纽备份的影响因素，以优化轴辐式网络构建成本和备份成本。

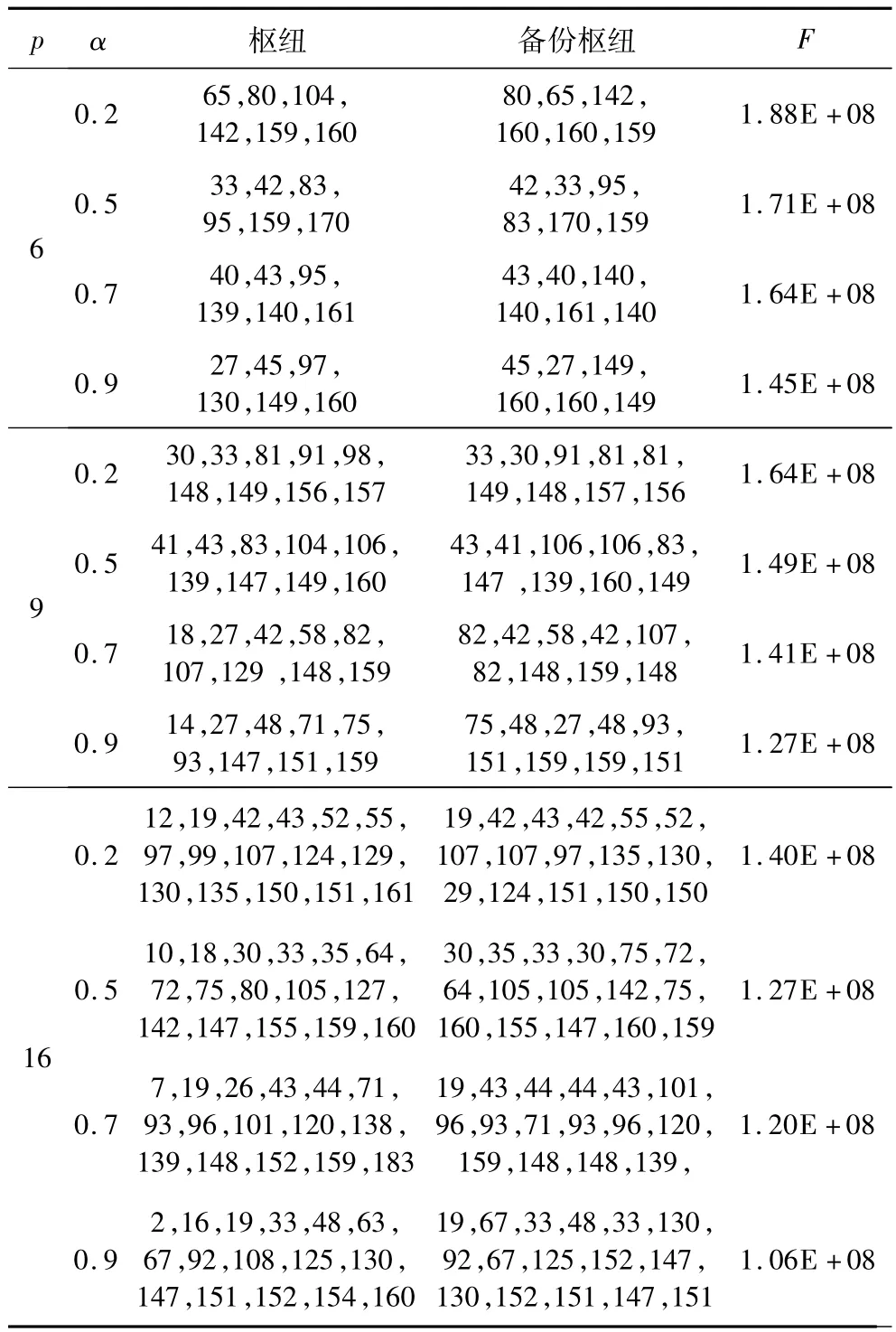
表5 遗传算法求解结果Tab.5 Solution result of genetic algorithm

提高物流系统的可靠性，需要有效的网络系统管理策略，如枢纽点备份。备份枢纽的研究在应急物流中的灾民疏散区选址、帐篷募集地设置、零担物流中的备用仓库选址都有实际的应用意义。接下来的研究可以从多个枢纽失效、多个备份枢纽方面进行，其中枢纽失效对枢纽通道的影响和恢复也值得进一步探讨。