基于BELLHOP模型的水下信道仿真方法研究∗
李 孟 周荣艳,2
(1.南阳理工学院 南阳 473000)(2.西北工业大学航海学院 西安 710072)
1 引言
随着水声信道建模技术的发展,衍生出很多建模技术,例如,抛物线方程法、波数积分算法等都是基于声传播的射线理论[1~2]。声场射线理论因其计算简洁,尤为适合求解和距离相关的声场环境的特点受到科研人员的追捧[3]。射线模型以声场中的声源和接收点为出发点,两点间的连线即为本征声线[4~5]。计算接收点上的声场就因此被简化了很多,只需知声源和环境文件即可通过两点之间形成的本征声线进行计算,这使得仿真的过程变得更加简单,并且只需要一个很小的基阵进行采样便可以达到观察大规模海洋声学特征的目的[6]。
基于声场射线模型的诸多特点,结合实际科研需要,本文采取基于BELLHOP射线模型的方法对水声信道进行仿真研究。本文在Matlab开发仿真平台上,对海洋水声环境中的声速剖面、几何结构、海底地形及声波在海洋界面中的反射和折射损失等各种相关参数进行输入和设置[7],通过基于Bell⁃hop模型程序的处理,得出海洋水声环境中水声声波的幅度、入射角和通信时延等信息。提取与传感器节点接收信号相关的传递函数参与运算,同时对声线数目的多少与传感器节点的最优节点放置之间的关系进行研究。
2 水下声场建模
2.1 BELLOP模型概述
BELLHOP模型是依据射线跟踪从而在海洋环境之中预测声压的模型,是由 Porter和 Bueker[3]在1987年编写的。这种射线跟踪结构使得其算法十分的简单,它是基于几何和物理的传播规律,可以实现包括高斯波束和帽形波束等多种类型的射线。BELLHOP能产生各种有用的输出信息,包括传输损耗,本征声线,到达和接收的时间序列等。BELLHOP模型在600Hz-30kHz的频率范围内的实验数据与理论模型比较相符,所以被指定为美国海军海洋预报10-100kHz频带声传播的标准模型[7]。使用BELLHOP模型对水声信道仿真能够有效地预测信道的数据以及工作性能。
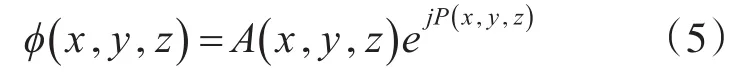
式(5)中P为程函,将这个解代入到Helmholtz方程中,并将实部与虚部分开,即可得到下面两个关系式:的乘积,即为
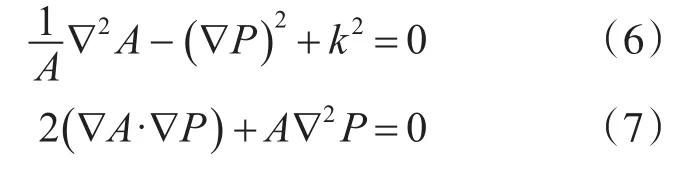
方程(5)为实部,确定声线的几何形状。方程(6)为虚部,确定声波的振幅,这种函数分离是在假设几何声学近似条件成立的情况下才成立。射线理论模型不仅考虑了本征声线,还考虑了折射-海面反射(RSR)、折射-海底反射(RBR)以及折射-海面反射-海底反射(RSRBR),为了考虑边界作用以及体积效应通常将海洋环境参数等物理模型并入到射线模型中[8]。
2.2 传递函数h(t)
在Bellhop模型中可对海洋水声环境中的声速剖面、几何结构、海底地形及声波在海洋界面中的反射和折射损失等各种相关参数进行输入及设置,得出海洋水声环境中声波传播的幅度和时延,由此得到从目标声源发射的信号到达传感器节点处的传递函数h()
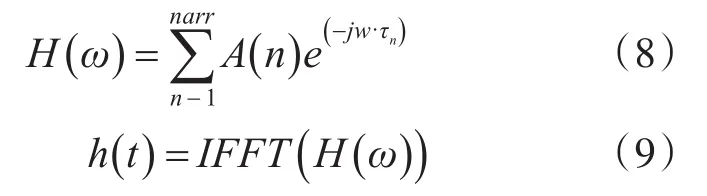
其中,narr表示到达的声线个数。
将传递函数h(t)与目标声源的发射信号做卷积,即可得到各个节点处的接收信号。若是对在Bellhop模型中提取的所有声线到达时延信息与幅度信息进行研究非常复杂且不现实[9],本文只考虑目标声源对应于传感器节点的所有路接收信号中的最大幅值,代表到达此传感器节点处的接收信号,对应于传递函数的最大值hmax。同时对于TOA之类的定位算法[10~11],只考虑节点处接收信号的最大幅度,也具有一定的现实意义。因此,本文中之后所用到传递函数h(t)均为hmax。
由上可知得到传递函数后,用传递函数与声源发射信号做卷积,可得到阵列输出信号,对阵列输出信号进行波束形成处理,得到波束形成图,通过波束形成的结果分析判断信号是否存在。在上述水声信道参数和传播参数条件下,得到的传递函数如图1所示。

图1 传递函数图
3 实验仿真
3.1 仿真参数设置
本节主要对基于BELLHOP的海洋声场进行仿真和分析。目标声源的信号参数如下:fc=1000Hz,Ts=0.005s,B=700Hz,信号1m处的信噪比SNR=70;
海洋环境参数和信号传播参数如下表1、2所示。
根据上述参数设置,由Bellhop模型仿真得到水下声线Munk图,如下图2所示。
由水下声线Munk图可知,声线的疏密表征声能的强度,声线会聚的地方声强大,声线发散的地方声强小[12],当声源在500m深度时,画出的传递函数h(t)等高线图与水下Munk图对比可发现,传递函数h(t)变化与水下声强的变化一致,即可用h(t)值来近似代表节点处于不同位置时接收信号的强弱。

表1 海洋环境参数表

表2 信号传播参数
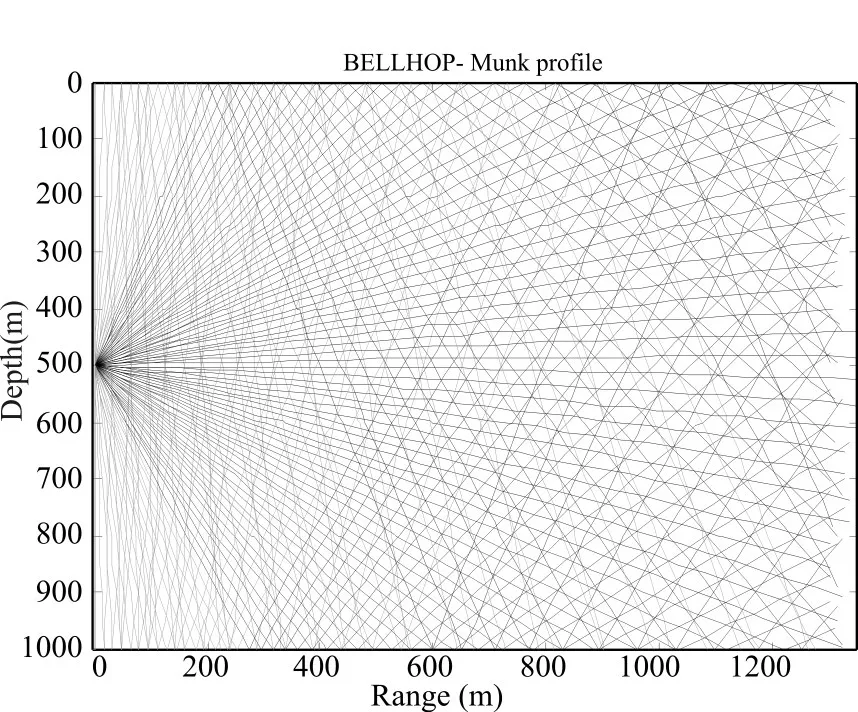
图2 Bellhop模型仿真得到水下声线Munk图
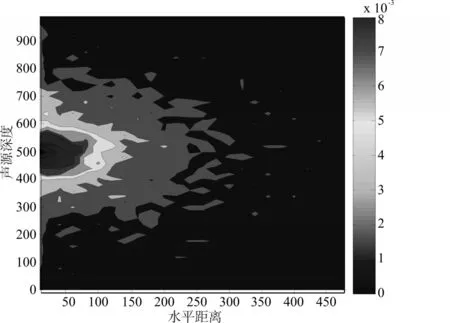
图3 声源深度为500m时传递函数h(t)等高线图
设声源深度范围为0~1000m,传感器节点的深度范围为0~1000m,声源与传感器之间的水平距离范围为0~1200m,设置间隔为10m,即以10m为间隔将声源深度、传感器节点深度和水平距离划分为101*101*121的矩阵,分别求出矩阵中的h(t)值,这样能够保证声源与传感器节点在不同深度和水平距离处,都可以通过临近的h(t)计算得到传感器节点的接收信号。
3.2 水下传感器节点的最优布局与声线数目的关系
在本文中主要考虑单个目标声源在Bellhop模型下的最优布局时与声线数目的关系,假定声源在[500,500]坐标处,选取5个节点采用遗传算法[]来进行布局。为了证明声线设置的多少对布局结果的影响,分别在Bellhop的*.env文件中设置声线个数为31条和161条来进行仿真。
声线数为31时优化布局结果如图4(a)所示。之后,将节点放置于声线图中,由于此时的声源为全向型点源,所以在*.env文件中设置发射角度为-180°~180°,此时声源位于500m的深度,在声线图中点源的位置坐标为[0 500],将节点的X轴坐标-500,Y轴坐标不变,将其表示在声线图中,如图4(b)所示。由图4(b)可知,最优布局时的五个节点坐标都位于声线上。
声线数为31时优化布局和与声线的关系如图4中(a)和(b)所示。
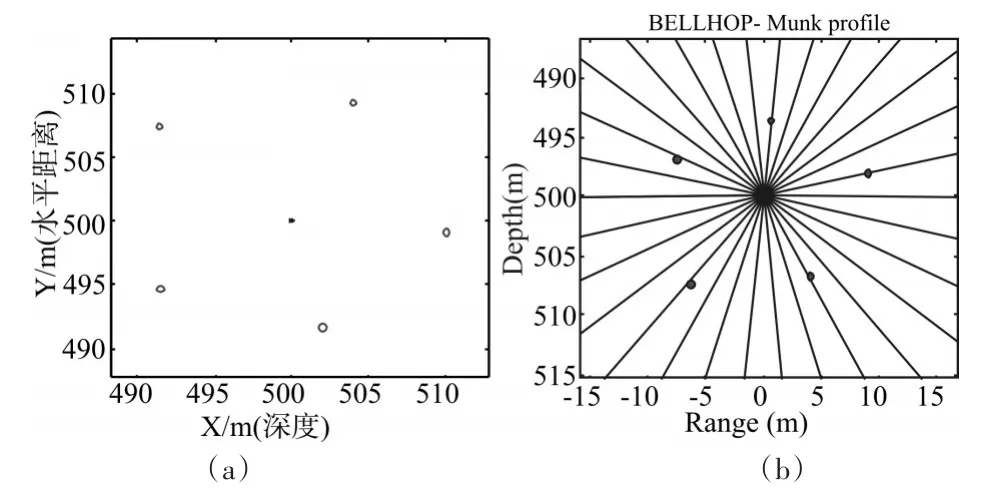
图4 声线条数为31时候的5个节点布局图和节点与声线关系图
设置同样的数据和条件,只是将声线数目变为161,节点布局图与声线图如图5中(a)和(b)所示。
由图4和图5可知,无论声线数目多少,优化布局的节点位置始终置于声线上。除此之外,针对于单个目标声源,选取5个节点采用自适应遗传算法对其进行最优布局,可从图中看出五个节点都布放于声源周围较近的位置,这一布局也符合文献[10]的结论。

图5 声线条数为31时候的5个节点布局图和节点与声线关系图
4 结语
本文主要基于BELLHOP模型对水下信道进行仿真,并研究分析目标声源探测的方法和阵列最佳布放方法与声线的关系。首先对水下声场建模基本原理进行介绍,利用BELLHOP模型对水下信道进行仿真并得到所需要相关输出参数,之后求得水声信道中声源到各个阵元的传递函数,通过改变声源位置参数,得到各组相应的传递函数。最后研究采用遗传算法的最优布局中节点的放置位置与声线之间的关系。仿真实验结果表明,采用传递函数能够很好地对水声信道中信号的传播途径模拟,此外,无论声线数目的多少,最优节点始终放置在声线上。

