基于粗糙集的航材保障效能评估指标体系优化

任佳成，徐常凯，张 昱

(1.空军勤务学院，江苏 徐州 221000；2.国防大学，北京 100858)

基金项目：空军航材库存清查及保障效能评估系统研究项目，项目编号：KJ2016A2163

0 引 言

从最近的几次局部战争可以看出，空军在当今信息化条件下的高技术战争中发挥着越来越重要的作用。其中，航材保障作为航空装备保障的重要组成部分，直接影响着空军的战斗力，其质量的优劣直接影响着飞机战训的完好性、持续性和效益性，也关乎着空军装备保障能力形成的快慢、保障效率的高低、综合战斗力的生成。

航材保障工作的评估一直是一项很紧迫的任务。但当前建立的航材保障效能评估指标体系较为繁琐，指标过多，存在一些等价的指标，造成评估过程繁琐，评估模型难以求解。因此，需要对当前构建的指标体系进行优化。通过采用粗糙集理论中的属性约简，应用基于该理论的航材保障效能评估指标体系优化方法，对保障效能评估指标体系各指标进行优化。

1 航材保障效能评估指标体系

空军航材保障效能评估指标体系的构建是开展评估工作的基础，指标体系能将一线实际问题与保障经验要求结合起来，满足部队保障评估的需求，并为制定航材保障质量评估规划文件提供蓝本。空军主战机型航材保障质量评估指标体系可以分为如图1所示的几个层次。

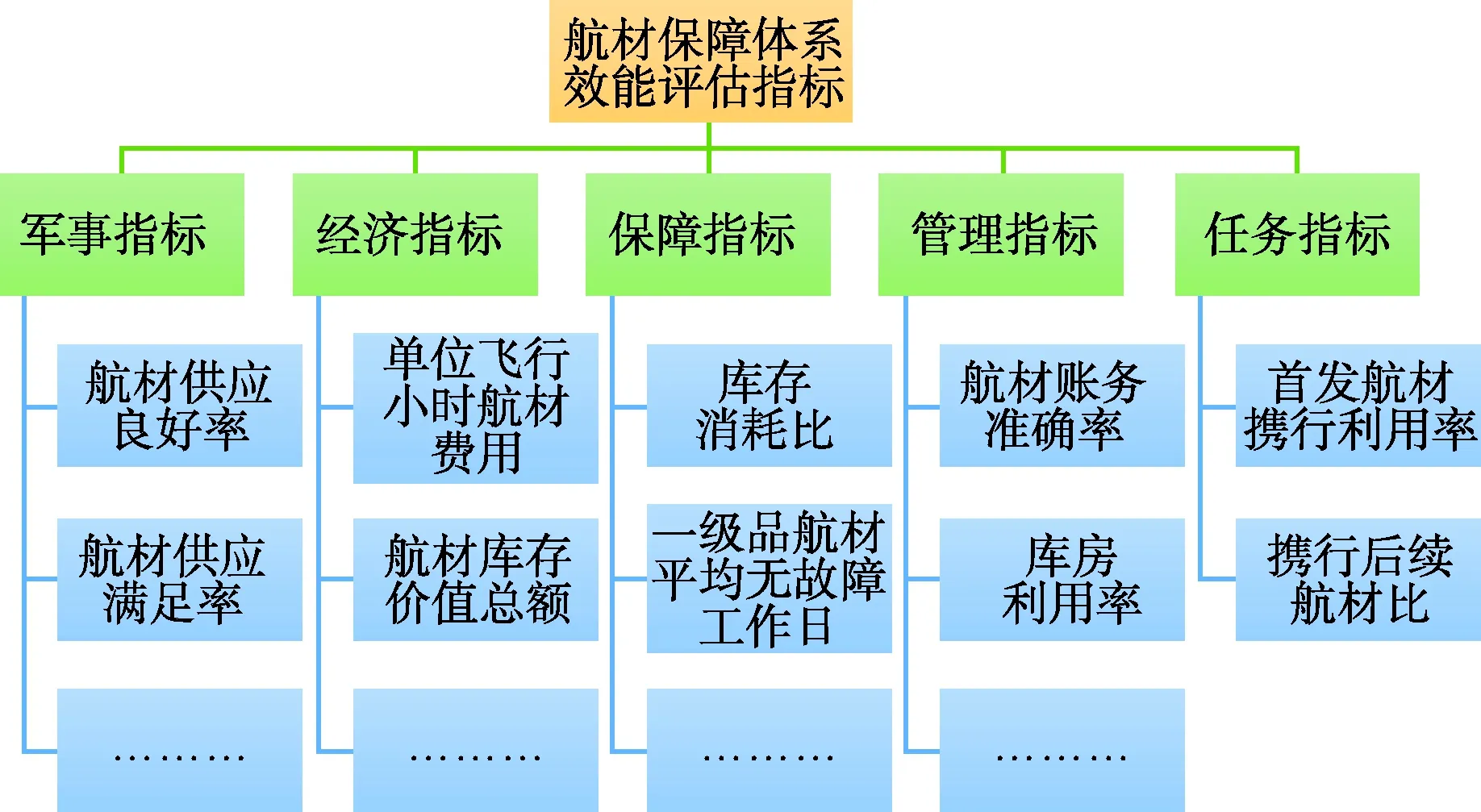
图1 空军主战机型航材保障效能指标体系

现行的航材保障质量评估指标体系还不够合理科学，评估机制还存在诸多的局限和弊端，在一定程度上阻碍了航材保障难题的解决，影响了空军装备保障工作的深入发展，突出表现在以下几方面：

(1) 评估的范围较为单一

当前主战机型航材保障中的问题是由多个部门、多个环节以及多方因素造成的，但现行的质量评估过于倚重航材部门的保障水平，而对与航材保障相关的非航材部门的工作质量评估得不够，致使保障质量评估的范围不够全面，影响了评估结果的客观性。

(2) 评估指标的可操作性不强

保障质量评估指标在设定时，不仅仅要考虑指标自身的科学性，更要兼顾能否有稳定的数据来源去支撑，否则就会严重影响指标的利用价值。但现行的评估指标中，数据收集的过程较为繁琐，且与航材管理信息系统中的数据信息对接不够，致使指标应用性不足。

(3) 评估指标的现实需求度不高

评估指标能否满足现实需求，是指标设置和存在的根本基础，同时指标还应能够根据形势变化情况，相应地进行补充或优化，以始终保证指标的前沿性。2006年确定的现行评估指标已沿用多年，如今部队状况、机关关注、战训需求均发生了极大变化，使得该指标体系与当前航材保障效能密切相关的指标设置得较少，在体系构成上与实际需求有所脱节，已不能适应当前实战化训练装备保障质量评估的需求[1]。

(4) 评估指标的分析角度较为单一

在分析航材保障质量问题时，应当坚持多角度、全方位、成体系的原则，从不同方面去看待、剖析和评估，这样得到的结论才能更加公正。但现行的评估指标中，对于航材保障中的某一项工作或某一环节工作的评估，角度过于单一，反映出的问题过于片面，造成了评估结果不够客观。

(5) 评估指标的计算模型不够具体

模型与方法是指标定量化的重要渠道，也是实现指标理论内涵与实际应用相互衔接的桥梁。但现行的评估指标中，部分指标的内涵表述不够准确，计算模型不够完整，统计方法与实际结合不够紧密或者操作性不强，造成了部分指标利用存在一定的障碍。

从这些问题可以看出：现有的航材保障质量评估指标体系已不能完全适应当前装备的管理要求。为了解决这个不适应，很有必要开展空军主战机型航材保障质量评估指标体系优化研究，以满足现阶段评价航材保障质量、发现航材保障问题、指导改进航材保障工作方法的需要[2-3]。

因而，确立航材保障效能评估指标体系的原则如下：

一是全面性。应针对所有的航材保障要素，综合考量，有针对性地提出评估指标，通过指标体系全面反映航材保障水平。

二是可操作性。空军航材保障效能评估指标体系，力求简明扼要，便于操作和测量，以利于评估计算。

三是独立性。组成保障能力指标体系的各指标，其定义应科学地反映航材保障某一方面的能力，防止因理解上的二义性而出现偏差。

研究分析目前空军各级航材保障单位的总体情况和实际需求，建立涵盖军事、经济、保障、管理、任务等5个大类的效能评估指标体系。

2 粗糙集(RS)约简算法

波兰数学家Z.Pawlak于1982年提出了粗糙集理论，它在处理不精确、不确定与不完全数据方面的问题，具有一定优势[4]。

在信息系统S=(U,A,V,f)中，|U|=n。属性集P⊆A的差别矩阵M(P)是一个n×n矩阵，其任一个元素为：

δ(x,y)={a∈P|f(x,a)≠f(y,a)}x,y∈U

(1)

因此，δ(x,y)是区别对象x和y的所有属性的集合。显然差别矩阵是一个对称阵。如果属性集A=C∪D,则可定义(C,D)差别矩阵，记为M(C,D)[10-11]。

(2)

在对差别矩阵进行的约简时，需要构建一个差别函数[5-6]，并用符号Δ来表示。设有∀a∈A，当存在δ(x，y)={a1，a2，…，ak}≠φ时，则构建一个布尔函数a1∨a2∨…∨ak，并用∑δ(x,y)来表示；当δ(x,y)≠0时，取布尔函数为1[7-8]。因此差别函数Δ可表示为：

(3)

应用布尔代数中的分配定律和吸收定律进行化简，得到差别函数Δ的析取范式。函数Δ的极小值析取范式中的所有合取式即为属性集A的所有约简[9]。

3 基于粗糙集的指标体系的约简

属性约简主要是将不可分辨关系进行比较，进而删去不必要的知识。

3.1 一级指标的约简

一级指标(军事、经济、保障、管理、任务)体系如表1所示。

表2是相关领域的6位专家分别对某航材保障中的5个一级指标的评分。评分采用5分制，其中，1分为不重要，2分为不太重要，3分为重要，4分为比较重要，5分为非常重要。

表1 指标体系表

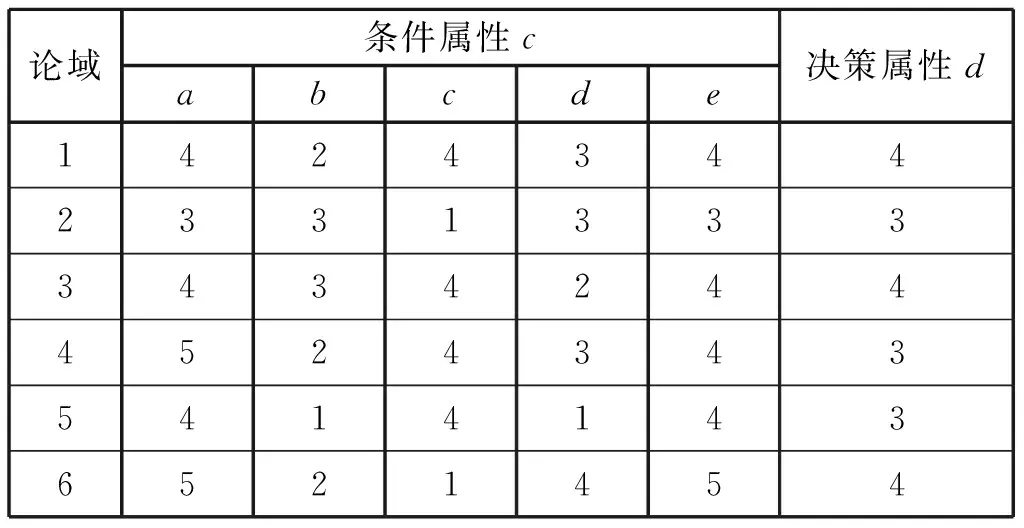
表2 属性信息表

对于表2给定的信息，首先进行属性的约简。为构造差别函数，先求取所有(x,y)的差别属性集合构成的差别矩阵。为了书写方便，条件属性分别用a,b,c,d,e表示，得到的对称差别矩阵见表3。

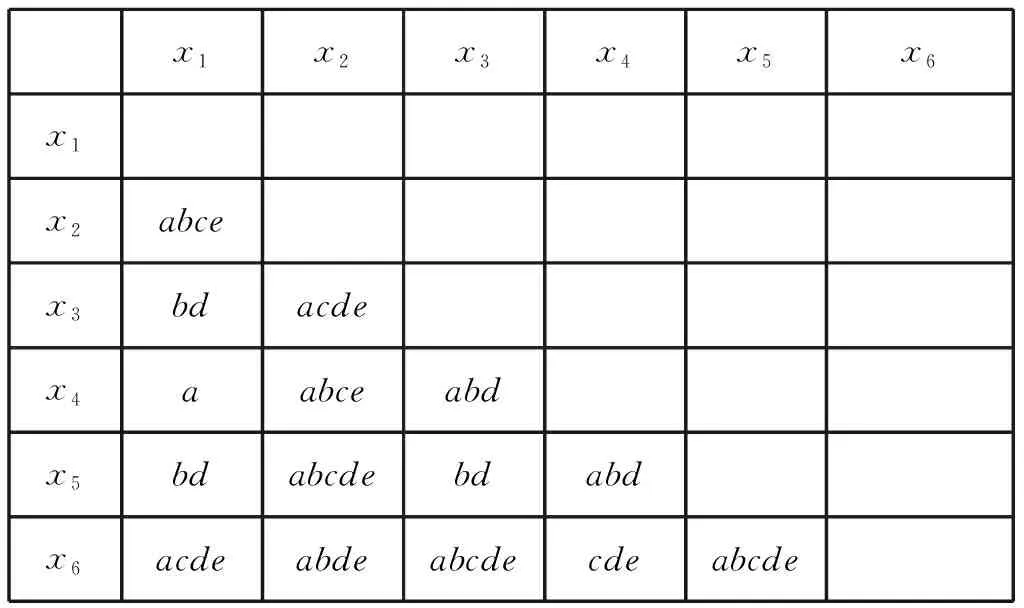
表3 差别矩阵表

对应的差别函数为：

Δ=(abcd)∨(bd)∨(a)∨(acde)∨(abcde)∨(abde)∨(abd)∨(cde)=a∨bd∨cde

(4)

综上所述，该系统的核为a，2个约简分别为{abcde}和{acde}。因此，评估指标为军事、经济、保障、任务，这样就实现了指标的选取与指标体系的优化。

3.2 二级指标的约简

由于航材保障效能评估指标体系指标众多，这里仅以使用航材保障军事指标(见表3)为例进行约简，现随机抽取10个航材保障单位(分别用xi表示)，对其航材供应保障数据进行统计分析，得到其军事性评价指标结果如表4所示(Ⅰ、Ⅱ、Ⅲ分别表示由高到低的3个等级)。

表4 军事指标

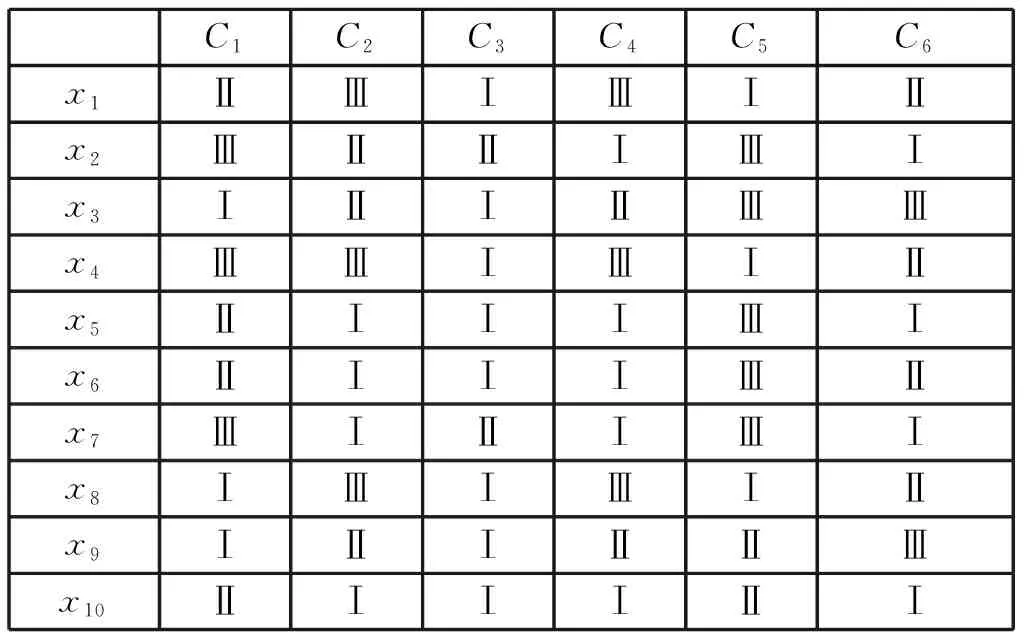
表5 初始信息系统

对于表5给定的信息系统，首先进行属性的约简。为构造差别函数，先求取所有(x,y)的差别属性集合构成的差别矩阵。为了书写方便，条件属性C1,C2,C3,C4,C5,C6分别用a、b、c、d、e、f表示，得到的对称差别矩阵见表6。

则信息系统的差别函数为：

fS=(a∨b∨c∨d∨e∨f)(a∨b∨c∨d∨e∨f)(a∨b∨c∨d∨f)a(b∨c∨d∨f)…=(abef)

(5)

由fS可知，系统有唯一约简{a,b,e,f}，即飞机完好率指标和缺材停飞率指标被约简了。但这并不意味着这2个指标不重要，可能这2个指标与前面几个指标具有一定的重合性，故舍去。

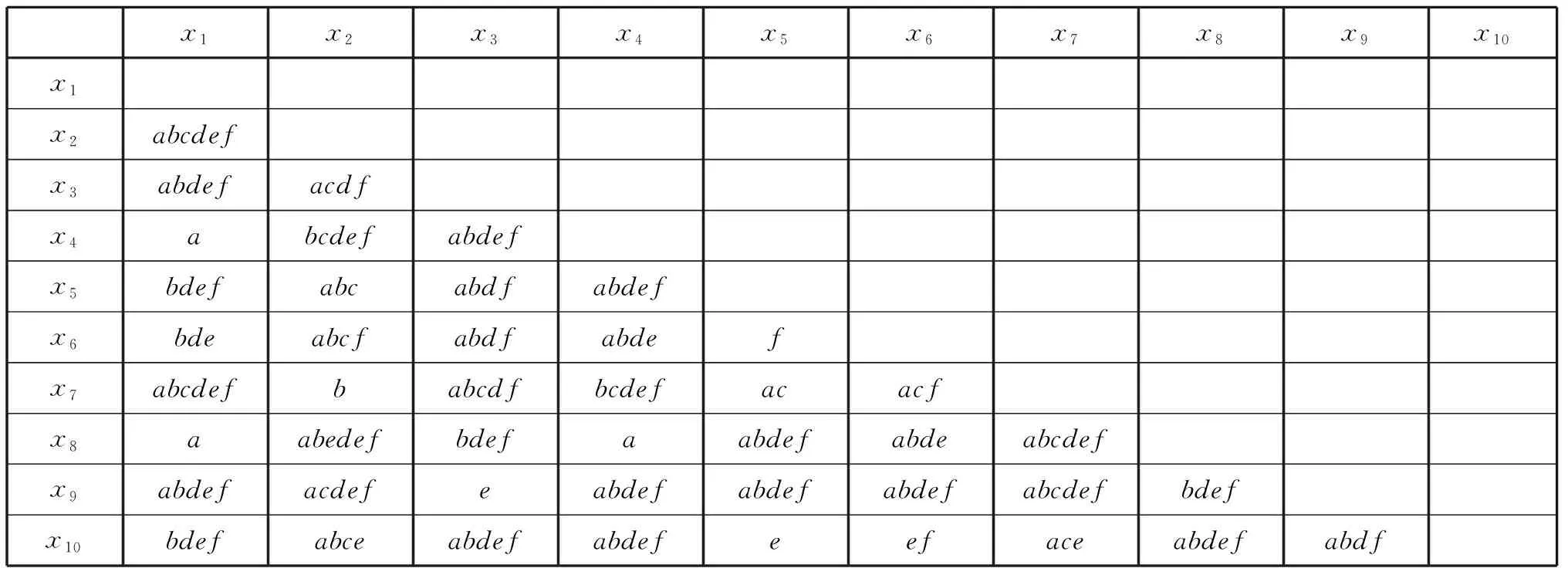
表6 差别矩阵

依次按照该步骤，对初始指标体系进行约简。

4 结束语

本文对粗糙集理论中属性约简算法在航材保障效能评估指标体系优化方面的应用进行了积极探讨。综合分析影响航材保障质量的核心问题，全面考量航材保障中筹、储、供、管、修等各环节，在国军标中挑选合适指标，并通过RS理论中属性约简的方法，优化了空军航材保障效能评估指标体系。新指标体系涵盖了军事、经济、保障和任务等各个方面。优化后的新指标体系已经在2017年空军航材新法规中得到应用。