自适应非相干矢量跟踪环路设计

刘红光 ，傅金琳，金 天，吴雨航，纪元法

（1. 天津航海仪器研究所，天津 300131；2. 北京航空航天大学电子信息工程学院，北京 100191；3. 广西精密导航技术与应用重点实验室，桂林 541004）

随着卫星导航在军民导航领域的普及，卫星导航弱信号、易被干扰的缺点受到国内外学者的高度关注，并展开了相关研究。

矢量频率/延迟锁定环路（VFDLL）是近些年来提出的一种接收机跟踪环路架构，相比于传统接收机环路，矢量跟踪环路不仅具有抗干扰性强、动态性能好、重捕速度快等优势[1]，甚至还可能在某几颗卫星信号突然消失时暂时保持跟踪状态。矢量跟踪环路的这些优点来源于矢量接收机处理信号的机制与传统接收机不同。在传统的接收机中，各通道信号完全独立处理，分别计算得到各自的伪距、伪距率，最后再进行导航滤波给出最终导航解算结果。而矢量跟踪环路融合了所有通道的信息，将信号跟踪环路和导航滤波器融合在一起，同时完成信号跟踪与导航信息解算。

国外针对矢量跟踪的研究起步较早，文献[2]提出了同时跟踪所有通道的矢量接收机的一种实现方法并给出了相应的理论分析。文献[3]在上述基础上给出了一种改进的矢量跟踪算法的实现方法。国内相关研究主要集中在矢量跟踪算法的优化以及实现上，文献[4]提出了基于快速相关的矢量跟踪算法，该算法可以使跟踪性能得到提升。文献[5]在矢量跟踪的基础上进一步进行了 SINS深组合，而文献[6]给出了类似技术的硬件实现方法，文献[7]则给出了文献[3]所述方法的性能分析。但上述研究几乎都基于传统矢量跟踪环路，仅单独在矢量频率锁定环或矢量延迟锁定环引入非相干计算，并没有给出非相干 VFDLL环路的实现方法。

本文在典型的矢量跟踪环路的基础上，引入了非相干频率/码鉴别器设计，并分析了采用非相干积分的矢量跟踪环路在灵敏度和动态性能上的提升，给出了不同环境下建议的非相干积分次数。

1 非相干频率/码鉴别器矢量跟踪环路

典型的矢量频率延迟锁定环路（VFDLL）的结构框图如图1所示。各个通道的中频信号I、Q支路分别与本地复现的载波、码进行相关运算后，进一步进行相干积分。再对k-1次和k次积分结果利用式(1)(2)进行频率和码鉴别[8]，最终得到的结果转化为伪距率误差S(f)和伪距误差后，作为观测量传递给矢量跟踪的卡尔曼滤波器（KF）

在上述结构中，利用相干积分的结果进行鉴相存在一定的局限性。

首先，接收机要通过相干积分过程获得载噪比提升，那么就要求在相干积分时间内不能够发生数据比特跳变，否则相干积分的结果很可能会正负抵消，从而减弱相干积分结果。这一特点限制了接收机相干积分的时间最长为一个数据比特时间。例如GPS L1CA信号的相干积分时间最长为20 ms，并且必须在实现位同步之后才能进行如此长时间的相干积分，而为保证在相干积分过程中不受比特跳变影响，在接收机实现位同步之前通常采用诸如 1 ms或2 ms等较短的积分时间。因此使用相干积分结果进行鉴别使得码跟踪和载波跟踪之间有相当大的相互影响[1]，令跟踪环路变得很脆弱。

第二，即便采用10 ms相干积分时间也要求环路中的卡尔曼滤波器（KF）要达到100Hz更新频率，这给整个环路带来了相当大的计算负荷，也给硬件实现带来了很大难度。

另外，由于我国北斗导航B1I信号同时播发50 bps和500 bps两种速率的信号[7]，仅仅使用相干积分来处理信号就会造成相干积分时间难以确定的问题。

因此，针对上述问题设计一种新的矢量跟踪处理算法是有必要的。

针对上述问题，本文提出了一种非相干结构的频率/码鉴别器（NC-VFDLL）结构，如图2所示。该结构对相干积分的结果再进行非相干运算，所得结果再进一步进行频率/码鉴别。由于非相干运算结果不再受到数据比特跳变的影响，可以进行长时间的积分运算以提高信号载噪比，使得环路灵敏度得到提高。另外，进行非相干预算后环路更新速率会得到下降，在一定程度上可以减小矢量跟踪环路计算负荷，降低矢量接收机的硬件实现难度。

图1 典型VFDLL环路结构Fig.1 Typical VFDLL loop structure

图2 NC-VFDLL环路结构Fig.2 NC-VFDLL loop structure

对于非相干频率鉴别器，可以利用k次I/Q支路相关结果的联合概率密度，通过极大似然估计得到次非相干的鉴相和鉴频结果，分别为[1]：

对于非相干码鉴别器，如式(5)所示[10]：

上述非相干处理算法将相干积分的结果进行平方处理，使其能够克服数据比特跳变带来的影响，可以实现较长的积分时间。

2 NC-VFDLL灵敏度和动态性能分析

2.1 非相干积分增益

非相干积分过程在一定条件下能够提高信号信噪比，是接收机实现捕获跟踪弱信号的重要技术之一。与相干积分类似，非相干次数为时相干积分的增益

其中，Ls代表信号进行平方处理带来的平方损耗（squaring loss）[9]，a为信号信噪比，I0、I1分别为零阶和一阶修正贝塞尔函数。

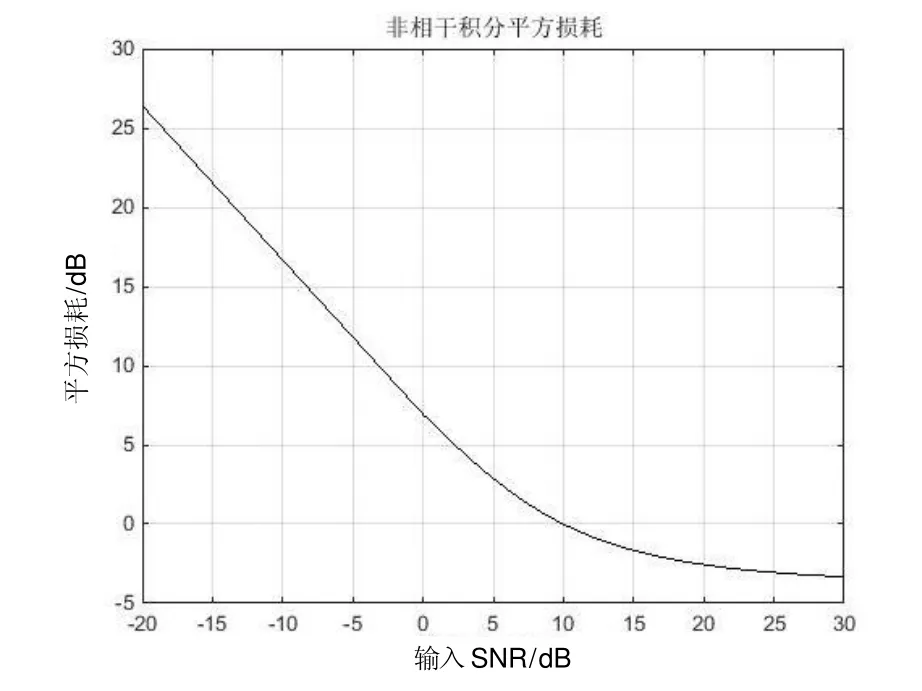
图3 非相干积分平方损耗Fig.3 Non-coherent integrated squared loss

平方损耗大小关于非相干积分输入信号信噪比之间的关系图如图3所示。可以看出，在输入信噪比较大时非相干积分带来的信号损耗较小，在输入信噪比较小时非相干积分带来的信号损耗较大。

2.2 NC-VFDLL环路建模

NC-VFDLL环路离散状态方程由式(8)给出：

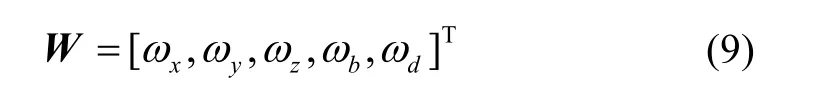
NC-VFDLL环路离散观测方程由式(12)给出：

其中：H矩阵取决于当前时刻载体与卫星之间的相对位置；为观测误差矩阵，均值为零，方差为鉴别器输出噪声方差。

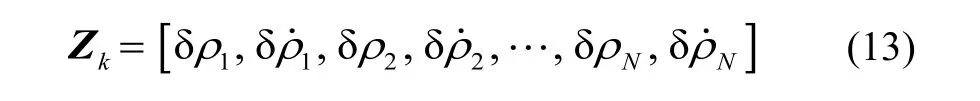
根据离散卡尔曼滤波方程，其估计均方误差为：

根据上述模型，在给定环路各项参数时可以计算得到环路误差。

2.3 NC-VFDLL性能分析

2.3.1 NC-VFDLL环路灵敏度分析

在研究 NC-VFDLL环路灵敏度与相干积分次数之间的关系时，假定卫星的几何分布确定，所有卫星信号同时到达接收机且估计误差的均方误差最小。为了排除载体动态对系统的影响，仅考虑静态场景下环路的跟踪误差。

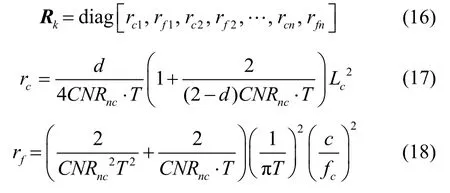
此时的环路误差跟踪误差为：

在相干积分时间为1 ms，VFDLL环路跟踪5颗星和10颗星时，进行不同次数非相干积分，环路稳定时多普勒误差与信号载噪比之间的关系曲线，如图4和图5所示。在相同相干积分时间下，随着非相干积分次数的增加，环路跟踪灵敏度有很大提升。

图4 跟踪5颗星时非相干积分次数对环路灵敏度的影响Fig.4 Influences that non-coherent integral times exert on loop sensitivity when tracking five satellites

图5 跟踪10颗星时非相干积分次数对环路灵敏度的影响Fig.5 Influences that non-coherent integral times exert on loop sensitivity when tracking ten satellites

2.3.2 NC-VFDLL环路动态性能分析

为了分析非相干矢量环路的动态性能，在载体动态模型中系统状态方程增加一个控制矢量：

图6和图7分别给出了在10颗卫星，相干积分时间1ms条件下，不同非相干积分次数时环路所能承受的加速度和加加速度与信号载噪比的关系曲线。图6 中环路驱动噪声方差10 m2/s4，图7中环路驱动噪声方差10 m3/s6。从图中可知，在相干积分时间一定时，环路能够承受的最大载体加速度、加加速度随着非相干积分次数的增加而增大，采用长达50次或100次非相干积分的环路动态性能要明显优于采用短积分时间的环路。在相干积分时间一定的前提下，随着环路非相干积分次数的增加，环路动态性能得到了一定的提高。

图6 不同非相干积分次数对环路加速度承受力的影响Fig.6 Influences that different non-coherent integral times exert on loop’s acceleration tolerance

图7 不同非相干积分次数对环路加加速度承受力的影响Fig.7 Influences that different non-coherent integral times exert on loop’s acceleration jerk tolerance

2.3.3 非相干积分与相干积分环路性能对比

在相同环路更新时间下，对非相干积分环路与相干积分环路之间的性能差异进行分析。图8和图9所示分别为静态和动态条件下，环路更新时间相同时采用相干或非相干积分得到的稳态误差分析结果对比。

当信号载噪比较低的时候，由于平方损耗较高，非相干积分环路的稳态误差显著高于相干积分环路；而当载噪比增大时，两者性能逐渐接近。在环路更新时间相同的情况下，使用非相干积分的环路灵敏度、动态应力误差均不如仅使用相干积分的环路，且载噪比越低二者差异越明显。

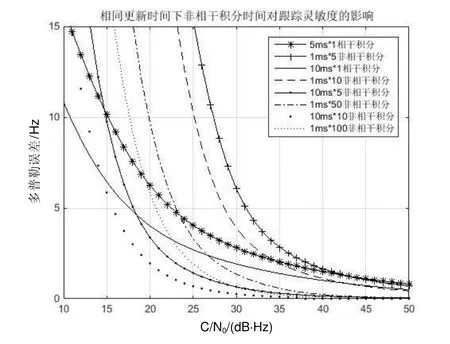
图8 更新时间相同时相干/非相干积分环路灵敏度Fig.8 Coherent/non-coherent integrated loop sensitivity with same updated time

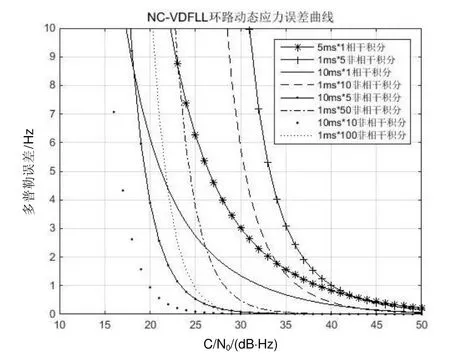
图9 更新时间相同时相干/非相干积分环路动态应力误差Fig.9 Coherent/non-coherent integral loop dynamic stress error with same updated time

图10和图11所示为相同环路更新时间下，使用相干积分和非相干积分的环路所能承受的最大加速度、最大加加速度曲线图，其参数设置与图6和图7对应。此时，环路能够承受的最大加速度和最大加加速度是使环路稳态误差满足式(24)时的最大加速度和加加速度：

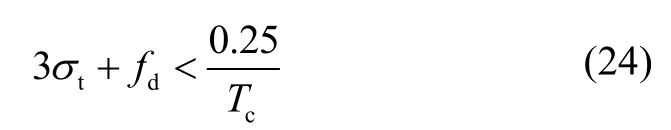
当信号载噪比较低时，曲线之间的差异更多的体现在非相干次数上，而在信号载噪比较高的时候，曲线之间的差异体现在环路更新时间上。图12中，当信号载噪比低于25 dB×Hz时，采用5 ms´1次、10 ms´1次、10 ms´5次、10 ms´10次仿真得到的四条曲线之间较为接近，而1 ms´5次、1 ms´10次、1 ms´50次、1 ms100次四条曲线可被划分为另一组。而在信号载噪比较高时，曲线按照走向应分为四组，也即按照环路更新时间5 ms、10 ms、50 ms、100 ms分为四组。

图10 更新时间相同时相干/非相干积分环路加速度承受力曲线Fig.10 Curves of coherent/non-coherent integral loop acceleration tolerance with same updated time

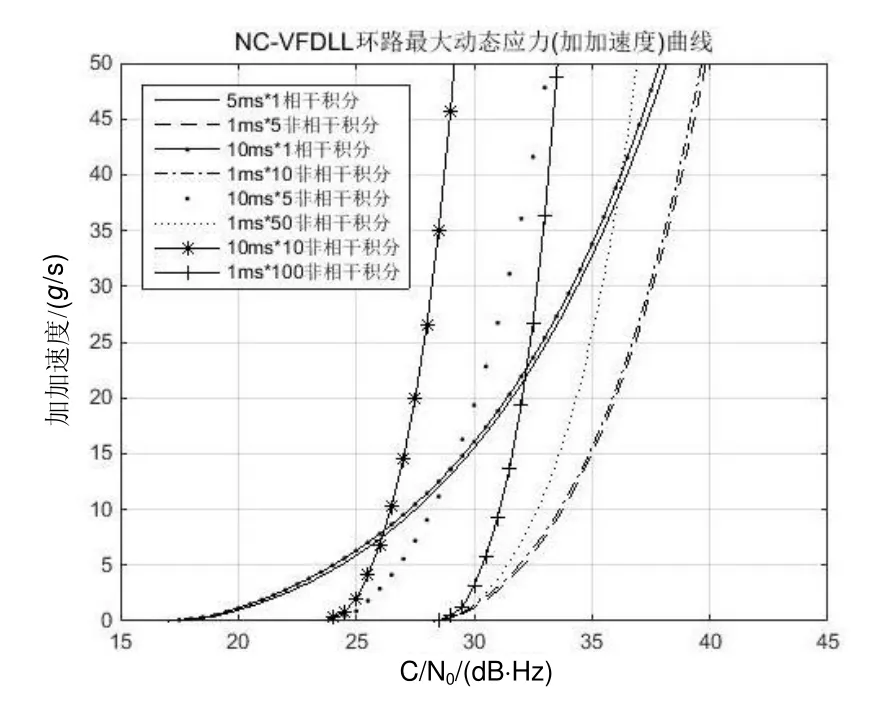
图11 更新时间相同时相干/非相干积分环路加加速度承受力曲线Fig.11 Curves of coherent/non-coherent integral loop acceleration jerk tolerance with same updated time

图10和图11的结果说明在给定环路更新时间的条件下，应该尽可能使用相干积分来实现性能的提升，而非相干积分的作用是进一步增加存在导航电文条件下的环路积分时间。例如在给定环路更新时间 10 ms时，10 ms´1次的环路性能要优于1 ms´10次的环路性能；在给定环路更新时间 100 ms时，采用 10 ms´10次的环路性能要优于1 ms´100次的环路性能。

3 矢量跟踪非相干次数优化

在一定条件下采用非相干积分增加环路更新时间确实能够提高环路灵敏度和动态性能，但是由于平方损耗的存在，在信号载噪比较低的时候采用非相干积分所得到的环路灵敏度和动态性能均有较大下降。另一方面，在NC-VFDLL环路中，环路更新必须要保持较快的速率以保障环路能够适应高动态效果。在实际设计中，只增加环路非相干积分次数并不能取得最好的效果。本节讨论对于不同动态性能要求时环路积分时间的选取，给出环路积分时间的自适应优化值。

根据图10的结果采取以下非相干次数优化原则：1）环路相干、非相干积分时间的选择必须使环路能够满足既定的动态性能要求；2）若有多种选择的情况下，尽量使环路更新速率更高。

根据上述原则，可以得到当信号载噪比在17 dB×Hz至 42 dB×Hz时，满足条件的环路非相干积分建议值（ms´次）如表1所示。

表1 不同条件下非相干积分建议值（ms´次）Tab.3.1 Proposed non-coherent integral values in different conditions

从表中可知，当信号载噪比较低时，若载体动态较低时，采用5 ms´1次的相干积分方案即可满足要求。但如果载体有一定的动态，那么由图10可知短的积分时间又无法保证跟踪误差要求，此时则应该采取非相干积分来延长环路积分时间使环路能够稳定跟踪，这时非相干矢量跟踪环路设计的意义尤为明显，如在50g加速度的高动态场景中，采用10 ms´5次的非相干积分相比10 ms´1次相干积分可获得约6 dB灵敏度提升。

4 结 论

本文在传统卫星导航矢量跟踪环路中引入了非相干频率/码鉴别器，通过非相干计算环路积分时间能够得到延长，使环路的灵敏度和动态性能有所提高。在相干积分时间一定的前提下，随着非相干积分次数的增加，环路跟踪灵敏度和动态性能均有提高。但在环路积分时间一定的前提下，由于非相干积分引入了平方损耗，导致采用非相干积分的环路灵敏度和动态性能有所下降，尤其是在信号载噪比较低的时候，环路性能下降十分明显。仿真结果表明，在实际设计中，对于高载噪比或低动态信号环境下，可以采取如5 ms´1次的传统相干矢量跟踪方法，而对于低载噪比、高动态信号环境则可以采取如 10 ms´5次或10 ms´10次的非相干矢量跟踪方法来提高跟踪效果。上述非相干方法（NC-VFDLL）对于进一步提高矢量跟踪环路性能，降低计算复杂度，具有广阔前景。