基于RDF图结构切分的高效子图匹配方法

关皓元，朱 斌，李冠宇，赵 玲

(大连海事大学 信息科学技术学院，辽宁 大连 116026)(*通信作者电子邮箱rabitlee@163.com)

0 引言

资源描述框架(Resource Description Framework, RDF)是经W3C认证的用来描述语义Web中机器信息的标准数据模型，SPARQL是面向RDF图的标准图查询语言[1-2]。模式匹配是SPARQL查询处理中的核心问题，其目的是在复杂的RDF图数据中快速地搜索符合查询请求的结果。也就是说，面向RDF图的模式匹配是在RDF数据图中搜索到同构于查询图的数据子图的遍历过程(图1)，因此，该问题也可以称为子图匹配问题[3]。随着RDF数据量不断地增加，RDF数据模型对语义数据的表示也更加复杂，由于查询图的复杂性以及RDF数据的海量性，在查询处理的过程中时间效率很难得到保证，因此，本文提出一种基于RDF图结构切分的高效子图匹配方法。

在关系模型中，一条RDF数据被定义为三元组〈s,p,o〉,其中，s(subject)是主题，p(predicate)是谓词，o(object)是宾语，谓词表示主题与宾语之间的语义关系。一个RDF数据集以图的形式表示，图中的顶点表示主题与宾语，而谓词被映射到连接两个顶点的有向边(主题指向宾语)上作为顶点之间语义关系的表示(图1数据图G)。

在SPARQL查询中，查询语句以三元组模式表示，一个三元组模式就是一个限制条件，与三元组类似，但顶点标签可以是变量(谓词为变量的情况极其罕见，因此在本文的讨论中被忽略)，而一组包含多个限制条件的SPARQL查询则以查询图的形式表示(图1查询图Q)。在简单的SPARQL查询中，可以将RDF图分为3种基本结构[4]，如图2所示，分别为链形结构、环形结构与星形结构，然而随着RDF数据大量被发布，SPARQL查询也随之变得越来越复杂，一个复杂的RDF图往往是由以上3种结构交互连接而成的。

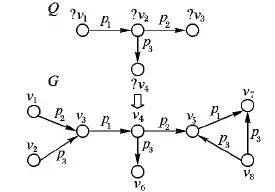
图1 面向RDF图的模式匹配

图2 RDF图的基本结构

RDF图结构的复杂趋势也导致了在查询中节点的选择性随之变差，在图结构足够复杂时，也使得子图匹配问题成为了NP-Complete问题[3]，以上两点使得面向图的查询处理成为了一项艰难的挑战。RDF- 3X[5]对此作出的对策是将RDF数据按照主题、谓词及宾语的选择性进行区分存储，分别设计了6个三元组表(spo,pos,ops,sop,pso,osp)，但是当数据量巨大的时候，表与表之间的跨表连接将产生很高的连接代价。而R3F[6]是将图形结构分解为以谓词为基准的路径，通过RDF数据之间的语义关系进行查询，但是采用将数据降维的方法在面向环路及星形图结构时，容易导致数据信息丢失从而降低了查准率。与上述两种方法不同的是，GraSS[3]则是从RDF图结构特征的方面入手，由于星形结构的组成往往是决定RDF图结构复杂程度的重要因素之一，GraSS将数据图中两两相邻的星形结构的公共节点作为特征项以建立基于hash编码的模式索引，但却忽略了链形结构与环形结构对查询过程中节点连接的影响。

基于此，本文通过发掘查询图与RDF数据图的结构与语义信息，建立一种高效地处理模式匹配的方法——RSM(RDF Subgraph Matching)。为了保证数据信息不丢失，在该方法中提出了基于分类学思想方法的RDF图结构切分规则并按照该规则将复杂查询图切分为多个简单查询子图，以便于降低整个执行过程的计算复杂度，其中，查询子图的匹配结果之间互相影响，从而提升了RDF数据的选择性。通过对RDF数据图的语义信息的分析，建立了相邻谓词结构倒排索引，用来定义查询子图的节点搜索空间，搜索空间中的节点称为查询节点的绑定节点。对比以往的单向谓词路径索引，本文同时考虑了数据图中的节点作为主题与宾语的不同谓词结构，该索引加快了节点的过滤且因为倒排索引的方便性与高效性，不会导致因为数据图结构复杂而产生巨大搭建代价的后果。在定义了节点初始搜索空间后，通过相邻的查询子图结构来缩小搜索空间的范围，在最终确定的搜索空间中寻找到节点所在的子图结构并作为查询子图的绑定子图。最后，将几个绑定子图进行连接并作为最终结果图输出。

本文的主要工作如下：

1)提出了相邻谓词结构索引。将数据图中的节点按照相邻谓词结构进行分类存储，以便于子图匹配中节点的过滤。

2)提出了基于中心覆盖节点的图结构切分规则。通过整数线性规划建模解决最小中心覆盖集合的选择问题以确定一个查询图中的中心覆盖节点集合，按照集合中的中心覆盖节点将查询图切分为若干查询子图。

3)提出了最佳连接顺序建模方法，并据此生成查询计划。在中心覆盖集合确定之后，需要计算查询子图与子图中节点的处理顺序，提出用于计算处理顺序的建模方法，并根据最佳处理顺序生成相应的查询计划。

4)方法与算法有效性实证的实验对比分析。采用真实世界数据集与合成数据集来进行广泛的实验来评估RSM方法的适用性与高效性，综合实验结果表明RSM的查询处理性能要高于RDF- 3X、R3F与GraSS[3]。

1 相关工作

子图匹配也称为子图同构问题，对该问题的研究已经成为了热点[7-8]。文献[9-10]提出了基于启发式规则的三元组模式重排序算法来解决此问题，但是在RDF图结构十分复杂的情况下，这种将图转化为RDF三元组的解决方案的效果并不理想。目前一些主流的方法是通过建立索引结构来解决子图同构问题。本文按照处理模型将其分为基于三元组的索引与基于图形结构的索引，详解如下。

1)基于三元组的索引。RDF- 3X是一种基于关系表的SPARQL查询引擎。它使用B+树作为基本索引结构，以三元组〈s,p,o〉中的元素分别作为索引基准与列表排序Key而设计了6种属性表来分类存储RDF数据，查询优化器将属性表的统计信息转换为连接树，连接树决定了查询性能，但是表中的元素自连接与表间的跨表连接会产生较高的查询代价，随着数据量变大，RDF- 3X的查询代价成指数增长。Jena[11]和Sesame[12]通过建立一张大型三元组属性表来存储RDF数据，在表中同时访问几个属性并将其进行聚类可以加快节点过滤并减少连接的次数，最后将结果存储在单个表中，但是它需要用户提供聚类决策并保留先前的查询日志，由于这种大型表的建立并不规范化，很容易导致连接过程中的控制与属性重复，从而产生较高的查询时间与中间结果冗余的情况。

2)基于图特征的索引。基于图结构的索引是在三元组的基础上添加了对于结构的考虑。GRIN(Graph based RDF INdex)[13]使用图分割技术并参考节点距离的信息来建立基于图查询的索引，索引结构是一个平衡二叉树，树中每个节点代表一个三元组；但是GRIN将索引保存在内存中，当数据量较大时，这种存储方式会产生高昂的代价。在Graph indexing[14]中，作者提出了“辨别比率”来计算子图的“辨别力”，当该子图的辨别力“很强”时，便以该子图作为特征索引。g-index具有较好的过滤性能，但是这种方法具有很高的局限性，它要求子图具有特点鲜明的结构，当子图选择性较差时，处理效果并不明显。GraSS重点在于处理星形结构的RDF图，将数据图中星形结构的子图的公共顶点作为特征项来建立基于hash编码的模式索引，通过在含有星形结构的查询图中搜索符合特征项的顶点来进行子图过滤，GraSS对于星形结构较多的图查询处理是十分高效的，但是当面对数据图或查询图为大量的链形结构与环形结构时，则没有具体应对的方法。RP-filter(RDF Predicate-filter)[15]和R3F采用了将图形结构分解为路径信息的索引方案，通过建立谓词路径索引将节点分类存储，索引是树形结构，树中的边代表路径，节点代表谓词。RDF图中的节点通过连接其的不同谓词分类存储在节点列表中；但是，这种方法将图结构分解为路径，容易导致原本的信息丢失，并且如果图结构十分复杂(存在环路或星形连接)，仅仅依靠谓词路径并不能完全过滤掉无用的中间结果。

基于对上述的问题分析，本文提出了基于查询图结构切分的子图匹配方法(RSM)以解决因RDF图结构复杂而导致RDF查询图与数据图中节点的选择性变弱从而产生大量中间结果冗余的问题。通过将查询图分解为结构相对简单的查询子图来增强子图与节点的选择性，并通过相邻谓词结构索引与查询子图的相邻结构加快节点的过滤过程。在RSM处理过程中所涉及到的相关定义与相邻谓词结构索引的建立将在第2章详细阐述。

2 基本定义与谓词索引

2.1 数据图与查询图

RDF作为一种概念建模的方式，其想法是将关于语义信息的陈述表示为形如主题-谓词-宾语的三元组(Subject,Predicate,Object)。在关系数据库中，由于谓词是具有指向性的语义关系词，RDF数据集被抽象为有向图，称为数据图，本文对数据图的定义如下。

定义1 数据图。数据图(图3)是一个RDF图G=(V,E,L,ψ)。其中：V是查询图中的顶点集合，E⊆V×V代表连接图中任意两个顶点的有向边的集合，L是顶点与边的标签的集合，映射函数ψ:V∪E→L。

图3 RDF数据图示例

SPARQL的基本访问模式称为元组模式，与RDF三元组相同的是，在关系数据库中，元组模式同样被抽象为有向图，而不同之处在于主题及宾语可能是变量，本文对于查询图的定义如下。

定义2 查询图。查询图(图4)可定义为五元组Q=(VQ,EQ,L,ψQ,vars)。其中：VQ表示查询图中的顶点集合，EQ⊆VQ×VQ代表连接两个顶点的有向边的集合，L是查询图中顶点与边的标签集合，映射函数ψQ:V∪E→L，vars表示图中变量的集合。

图4表示的是与图3中数据图所对应的查询图。其中，顶点是变量，〈?v1,p2,?v2〉是一个三元组模式。从图4中可以看出，数据图中的三元组〈v4,p2,v7〉是三元组模式〈?v1,p2,?v2〉的一个匹配答案，本文将匹配答案称为绑定，与查询图结构匹配的数据子图称为绑定子图。

定义3 绑定子图。查询图Q的一个绑定子图(图5)B=(VB,EB,L,ψB,S)。其中：满足Q的单映射函数f:VB→VQ,且VB⊂V；映射函数ψB:VB∪EB→L，L是绑定子图中顶点与边上标签映射的集合；S是查询子图中各节点的搜索空间，VB∈S。

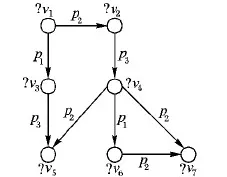
图4 查询图示例

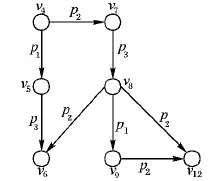
图5 绑定子图

2.2 相邻谓词结构索引

本文根据查询图与数据图中节点相邻谓词结构来定义查询图中节点的初步搜索空间，并将搜索空间中的节点称为绑定节点。数据图与查询图中的节点相匹配的节点相邻谓词结构必须是相同的。

定义4 绑定节点。与SPARQL查询所对应的RDF图节点绑定为Ans(Q)={θ|θ(GQ)}，其中GQ是G的子图同构；对于v∈VQ,Ans(Q,v)是v在Q上的映射，Ans(Q,?v)={θ(v|θ∈Ans(Q)},θ(v)将θ映射到v上;相邻谓词结构P(p|v)表示节点及其传入(节点为o)或传出(节点为s)谓词结构。

这里需要注意，因为谓词具有指向性，数据图中会存在入度或出度为0的节点，因此本文同时考虑了顶点作为主题与宾语的两种情况而分别提出了基于传出和传入谓词结构的顶点倒排列表，如表1所示。

表1 基于传入、传出谓词结构的顶点列表

根据表1中的数据可进行查询图中节点的过滤，图4中节点?v2的传入谓词结构为p2，因此可在表1中找到?v2的搜索空间S1(p2|v3,v6,v7,v12,v15,v18)，而?v2具有传出谓词结构p3，在表1中找到?v2的搜索空间S2(p3|v1,v7,v11,v13)，综合S1和S2将搜索空间压缩，最后找到符合子图同构的?v2绑定节点为v7；同理可得到查询图Q中其余顶点的搜索空间为:S(?v1)={v4,v8,v11},S(?v3)={v5,v11},S(?v4)={v8},S(?v5)={v6,v12},S(?v6)={v2,v11,v14,v17},S(?v7)={v3,v6,v7,v12,v15,v18}。

当查询图中节点较多且结构复杂时，一个查询子图中的节点可能存在多个绑定，将查询图作为整体进行谓词结构匹配的方式较为繁琐，在第3章本文将会介绍基于查询图切分的子图匹配方法，通过查询子图的相邻子图可以进一步缩小搜索空间。

3 RSM-查询图切分方法

3.1 查询图结构切分

RSM的核心在于将查询图分解为若干个结构简单的查询子图，本文给出的分解规则如下：选取中心覆盖节点，将该节点及其相邻节点划分为一个查询子图，若两个相邻节点与中心节点构成封闭图形，则子图中包括该图形。对于中心覆盖节点的选择，要求按照其划分的查询子图能够覆盖全部查询图以确保RDF数据不被破坏。

定义5 查询子图。查询图Q的一个查询子图q=(M,N,T)。其中，M是中心覆盖节点集合且M⊂VQ；N是中心覆盖节点的邻居节点集合且N={?v|?v∈VQ∩(?va,?vb)∈EQ};T是连接中心覆盖节点的两个邻居节点的边界集合，T={tn|tn=(?va,?vb),T⊂Q且tn∈EQ}。

如图6所示，图4查询图被分解为3个查询子图q1、q2、q3。左侧查询图中RDF节点?v2、?v3以及?v4为中心覆盖节点，即中心覆盖集合M={?v2,?v3,?v4}。在查询子图中，中心覆盖节点是图形中心点，且要保证RDF信息不被破坏，要求查询图中的所有节点至少被一个查询子图所覆盖，限制条件如下：

∀{?va,?vb}∈EQ⟹ ?va∈M∪?vb∈M

(1)

∃{?va,?vb},{?vc,?vb}∈EQ⟹ ?vb∈M

(2)

其中：式(1)确保查询图中任意一条边至少被一个查询子图所覆盖；式(2)确保了中心覆盖节点是查询子图的中心节点。查询图结构分解之后的查询子图可对进一步缩小节点的搜索空间提供帮助，3.2节将对此进行详细阐述。

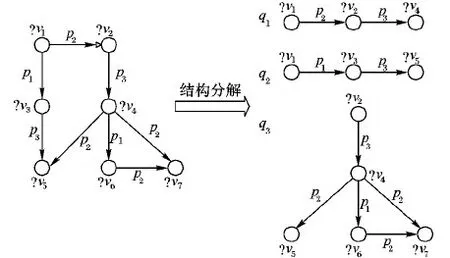
图6 查询图结构切分

3.2 缩小搜索空间范围

基于传入和传出谓词结构顶点列表可以确立查询图中节点的搜索空间，但是当数据图数据量较大时，某一节点的搜索空间范围很大，例如查询子图q2中，?v3搜索空间为S?v3={v5,v11}，有两个节点符合?v3相邻谓词结构，当?v3→v5时，其绑定子图的相邻节点为v4,v6，当?v3→v11时，其绑定子图的相邻节点为v10，v12。也就是说，仅仅从顶点列表中进行节点过滤，q2的绑定子图有两个，这时需要考虑相邻子图结构，若一个查询子图中的节点出现在其相邻子图中，那么该节点的搜索空间中的绑定节点必须同时满足两个子图结构，本文称其为公共节点特征。

定义6 公共节点特征。令(?va,?vb)∈Eq1,(?vc,?vb)∈Eq2,q1与q2为相邻查询子图。当q1→g1,q2→g2且g1与g2为相邻子图,并满足(?va,?vb) → (va,vb),(?vc,?vb) → (vc,vb)时，∃(va,vb)∈Eg1且(vc,vb)∈Eg2。

图7展示了根据公共节点特征进行特征搜索的过程，g1，g2分别为q2的两个绑定子图(曲线1所示)。为了进一步缩小搜索空间，需将其与相邻查询子图比较(曲线2所示)，如图可知q1与q2中存在公共节点?v1,因此将q1定义为q2的邻域子图，在q1中，?v1的搜索空间为{v4,v8,v11}，前文通过?v3确定了?v1的可能绑定节点为v4,v10，因此从这两者可得出v4是?v1的绑定节点，进而确定?v3的绑定节点为v5。

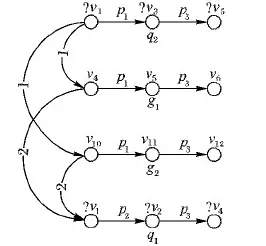
图7 特征搜索

在确定了q2的绑定子图后，根据其相邻结构，可快速缩小q1、q3的搜索空间并最终找到其绑定子图，这也体现了RSM的优势所在，不需要将查询图整体作为搜索单位，而只取其一部分简单结构即可找到与其相邻的查询子图的绑定子图，进而确定查询图的同构子图。与传统的模式匹配方法相比，可大幅度提升查询效率；但是在处理过程中需要注意一点，一个查询图中可能存在不同的中心覆盖集合，这也导致了搜索空间的处理过程不同，从而产生不同的查询代价。在3.3节会给出最小中心覆盖集合的计算及处理过程。

3.3 最小中心覆盖集合的计算

由于中心覆盖节点的选择不同，一个查询图可以有多种切分方式，进而存在同个查询图中出现多个中心覆盖集合的情况。例如图6中查询图的一个中心覆盖集合M1={?v2,?v3,?v4}，从图中可以发现M2={?v1,?v2,?v5,?v6}同样符合中心覆盖集合的条件。这里需要进行最小中心覆盖集合的计算，要求集合中节点数量尽可能最少，并且要保证查询子图完全覆盖查询图，即任意两个相邻的查询子图必须存在公共节点。计算最小中心覆盖集合问题属于图结构搜索问题，这类问题是NP-hard[16]，本文将其建模为整数线性规划(Integer Linear Programming, ILP)问题，建模如下：

(3)

(4)

n∈{0,1};?v∈VQ

(5)

其中n是二进制数，当?v是中心覆盖节点时，n=1，否则为0。式(3)使中心覆盖集合M中节点的数量最小化；式(4)确保了两个相邻子图的中心覆盖节点必有公共邻居节点存在；式(5)给出了n和?v的取值范围。

以图4的查询图为例，基于ILP建模的最小中心覆盖集合的计算过程如下：

minimizen0+n1+n2+n3+n4+n5+n6

s.t.n0+n1≥1; {?v1,?v2}

n0+n2≥1; {?v1,?v3}

n1+n3≥1; {?v2,?v4}

n2+n4≥1; {?v3,?v5}

n4+n3≥1; {?v5,?v4}

n3+n5+n6≥1; {?v4,?v6}

n3+n6+n5≥1; {?v4,?v7}

n5+n6+n3≥1; {?v6,?v7}

∀i,0≤i≤6,ni∈{0,1}

虽然对于图的最小中心覆盖集合的计算问题为NP-hard，但是对于具有几十个节点和几百条边的复杂查询图来说，计算时间是合理的。例如对于300个节点和1 800条边的查询图来说，不到6 s的时间内即可计算出其最小中心覆盖集合。

对于一些结构简单的RDF图来说，中心覆盖节点的选择相对容易，比如图2中链形结构的查询图是由节点串联表示的路径图，如果链中节点个数为奇数，则从起点开始偶数节点即为中心覆盖节点，奇数节点则相反；对于简单环路(三角形)而言，图中任意节点即为中心覆盖节点。式(6)和(7)分别给出了一个查询图满足链形结构与环路结构的条件：

|EQ|=|VQ|-1

(6)

|EQ|=|VQ|(|VQ|-1)/2

(7)

对于星形结构而言，图中节点与边的关系要满足式(6)，并且图中必定存在中心节点，即与其他节点均有谓词表示的关系，那么中心节点即为星形查询图的中心覆盖节点。对于星形图的中心节点的定义如下。

定义7 星形图中心节点。星形查询中存在节点vc，使得(vc,n)∈EQ，n∈Vm成立，其中Vm为查询图的其余所有节点的集合，那么vc即为查询图的中心节点。

在RDF图上的查询过程可以看作在匹配节点间进行连接的操作，并将执行计划的输出形式表示为二叉树，其中二叉树的叶子是节点，而父亲是叶节点间的连接操作(如图8)。整体的查询计划的输出形式为左深二叉树，这样做的目的在于每个父亲节点的右孩子即为下一个待查询节点。

子图匹配的效率往往取决于查询图中节点的处理顺序。例如图4的中心覆盖集合M={?v2,?v3,?v4}，集合中的每个节点代表其所在的查询子图，在集合M中，子图处理顺序有6种，每种顺序产生的执行代价有所不同。在第4章将会对计算最佳执行顺序作出详细阐述，并依照该顺序生成相应执行计划的执行算法。

图8 查询执行计划

4 生成查询执行计划

4.1 计算最佳子图处理顺序

本节主要对于最佳子图处理顺序的计算作出详细论述，本文将查询计划表示为查询图的节点连接过程，图4的中心覆盖集合M={?v2,?v3,?v4}的以中心覆盖节点为单位的查询计划为ψM=(?v2⊗?v3⊗?v4)=((?v2⊗?v3)⊗?v4),将查询计划展开，得到ψM=(?v1⊗?v2⊗?v3⊗?v5⊗?v4⊗?v6⊗?v7)。因为3个查询子图之间均存在公共节点，因此这样的连接顺序有6种(3个中心覆盖节点的排列组合)，分别为：ψM1=(?v2⊗?v3⊗?v4)，ψM2=(?v2⊗?v4⊗?v3)，ψM3=(?v3⊗?v2⊗?v4)，ψM4=(?v3⊗?v4⊗?v2)，ψM5=(?v4⊗?v2⊗?v3)，ψM6=(?v4⊗?v3⊗?v2)。对于该问题的计算，本文将采用GraphQL[17]与SG-Match[16]所设计的成本模型，该模型基于对贪心算法的修改，基本单位为单个节点，将搜索空间中绑定节点数量最小的节点作为当前处理节点。由于RSM采用将查询图切分的方法，基本单位不是单个节点而是整个查询子图，需要通过计算查询子图的整体代价，再计算查询子图中的节点处理顺序，因此修改为如下代价模型：

|Ψ(?vi)|=|?vi|/(|qi|+|qj| )

(8)

Cost(oi)=Cost(|ψ(?vi)|×|ψ(?vj)| )

(9)

Cost(oi×?vk)=Cost(oi)×|ψ(?vk)|×γx

(10)

其中：式(8)用于计算待查询节点的代价，是其搜索空间中绑定节点数量与该节点所在查询子图中节点数量的比值，qj是否存在取决于节点是否为公共节点；式(9)用于计算前两个待查询节点连接的代价；式(10)用于计算后续待查询节点连接的整体代价；γ是影响因子，当执行计划中待连接节点过多时，为了防止数据量过多而导致计算结果过大，将γ设置为2，这使得计算过程得到最好的结果；x是后续节点?vk的先前节点数量。

以查询子图q1的计算过程举例，q1的查询代价可表示为ψq1=(?v2?v1?v4)，基于本文的代价模型，首先需要计算查询子图中每个待查询节点的代价，再计算整体代价。为了提高处理的效率，节点的搜索空间定义为初次搜索空间，即根据前文设计的顶点列表来计算与查询节点对应的绑定节点数量，而不参考图形结构。根据代价模型得出查询子图q1、q2、q3的处理代价：

ψq1=(?v2⊗?v1⊗?v4)=0.17

ψq2=(?v3⊗?v1⊗?v5)=0.89

ψq3=(?v4⊗?v2⊗?v5⊗?v6⊗?v7)=1.92

根据计算结果可知，查询图q1、q2、q3的最佳执行计划为ψM=(?v2⊗?v3⊗?v4)。

4.2 生成最佳执行计划

在得到查询子图的处理顺序之后，需要计算单个子图内节点的处理顺序，本文采用了GraphQL的计算模型，该模型采用贪心算法的思想，将子图内绑定节点最小的作为当前处理节点，比如q1中?v2和?v4都只含有一个绑定节点，因此可将二者之一作为首处理节点。据此提出算法1作为执行计划。

在算法1中，首先初始化当前子图位置，当前节点位置与匹配结果集F，调用MinimalCostSG方法，从查询计划中获取子图顺序(第1)～3)行)。然后获取当前查询图q1，调用MinimalCandidateNodes方法，从q1中获取当前绑定节点数目最小节点，从搜索空间S中获取其绑定节点并存储与F中(第5)～10)行)。之后获取下一节点并重复此工作，直到j到达q1的最后一个位置并溢出，此时一个查询子图中的节点已完全匹配，此时调用UpdateS方法，通过匹配节点来更新其余节点的搜索空间并将i推向下一位置来获取q2，初始化j(第12)～15)行)，返回第2)行。当i的位置溢出时，说明全部的查询子图已经处理完成，匹配结果集F中已存在各节点的绑定节点，之后根据数据图及查询图的结构再一次过滤多余节点，最后得到精确结果并输出(第16)～20)行)。算法1的时间复杂度取决于输入的中心覆盖集合中节点的数量，其中m为中心覆盖集合中的节点数量。算法1展示了RSM的整体处理流程，这里需要注意一点，因为将中心覆盖集合M以及查询计划ψM作为算法的输入，而在子图及子图中的节点的选择过程中，本文采取了贪心算法的思想，及在查询计划ψM中选择当前处理子图，再在待处理子图中以当前绑定节点数量最小的节点作为子图中当前处理节点，基于贪心算法的思想将子图与节点的处理顺序按照其选择性强弱进行排序，以使得生成的执行计划是最佳的。

算法1 RSM执行计划。

输入:数据图G,查询图Q,中心覆盖集合M,查询计划ψM,搜索空间S,子图当前位置i,子图中节点当前位置j。

输出:匹配结果集F。

1)

initializationi=0,j=0,F={} then

2)

leti→qi,j→vj

3)

qi→ getMinimalCostSG(ψM) then

4)

foreachvj∈Vdo

5)

ifvj∈qido

6)

v=vj→ getMinimalCandidateNodes(Q,G,Sj) then

7)

v→F;F→Sj

8)

j=j++

9)

return then

10)

back to step 5)

11)

elsej=j++

12)

untilj=|qi| do

13)

i=i++,j=0

14)

Sj=S→ getUpdateS(vj,sj) then

15)

return then

16)

back to step 2)

17)

untili=|ψM| do

18)

returnF→ getUpdateF(G,Q,S) then

19)

OutputF

20)

end

5 实验结果与分析

5.1 实验环境与数据集设置

本文的实验设备采用Windows 7 64位系统，CPU采用Intel Core i5- 4200M@ 2.50 GHz，内存为8 GB，采用Cassandra(可快速处理大规模图数据的关系数据库)作为RSM的底层数据存储。

本文将RSM与RDF- 3X、R3F、GraSS对于结构复杂程度不同的查询图的查询响应时间进行对比，实验将分别采用合成数据集SNIB(社交网络基准http://www.w3.org/wiki/Social_Network_Intelligence_BenchMark)与真实世界数据集YAGO2[18]。其中，合成数据集SNIB源于社交网络，例如Facebook、Google Intelligence等，该数据集中的RDF图结构包括链形、环以及星形等若干基本结构所组合成的复杂结构；而真实数据集YAGO2是从维基百科、WordNet[19]衍生的知识库，该数据集的RDF图包含960万个节点和3 300万条边，其提供的数据集更接近于真实查询。

5.2 实验分析

一共做了两个对比实验，实验过程采用控制变量法，在不影响节点过滤的情况下，将相邻谓词结构索引进行压缩，使其大小近似于RDF- 3X的三元组属性索引以排除因索引的较大差异对实验结果的影响(R3F同样不考虑标签值，可排除索引影响，GraSS只针对星形图建立索引，普遍性与适用性不如RDF- 3X)，仅通过改变查询图中的结构复杂程度来比较3种方法的查询响应时间。图9表示了相邻谓词结构索引经压缩后与R3F、RDF- 3X、GraSS的索引大小比较，从对比图中可知，经压缩后的相邻谓词结果索引的大小随着三元组数据量增多的上升趋势与RDF- 3X、R3F近乎相同，且在数据量相同的情况下，索引的大小差距小于50 MB，因此对内存配置的要求也近乎相同，由于GraSS重点针对星形RDF图来建立索引，因此在数据集中存在的链形结构与环形结构数量任意的情况下，其索引在一般情况下是最小的。

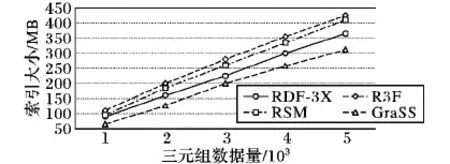
图9 索引压缩对比

本文以每组SPARQL查询中的元组模式数量来表示查询图的复杂程度，一组SPARQL查询可处理为一个查询图，元组模式的数量范围区间为[3,15](称为查询图复杂度)。在SNIB和YAGO2数据集中：查询图尺寸为3或4时，查询图结构往往为链结构与环结构，有少量的星形结构出现；当查询图尺寸为5以上时，会频繁地出现组合结构。对于每个查询图尺寸，本文从两个数据集中分别随机设置20个查询图与之对应，以保证查询图结构的随机性与复杂性。本文共设置了两个实验，实验1采用了SNIB数据集，实验2则采用YAGO2数据集，实验1与实验2的对比结果分别对应于图10(a)与图10(b)。

图10(a)显示了实验1的对比结果，当查询中的元组模式数量较少(生成的查询图结构相对简单)时，RSM的查询响应时间要稍慢于R3F，而RDF- 3X和GraSS在元组数量较少时的响应时间要长于RSM，当元组数为3时，查询图结构大多为链查询或少量的环查询，因此可以看到元组数从3提升到5(出现了组合查询)的时候，RSM的响应时间减少了0.08 s(表3)。而GraSS对于链形结构与环形结构并没有采取有效的处理措施，因此在查询图复杂度升高后，对于复杂查询图的处理效率提升得并不明显，随着元组模式数量的增多，RSM查询响应时间的上升趋势要远小于RDF- 3X、R3F与GraSS，因此，RSM在SNIB数据集上对于结构复杂的查询图的查询处理效率是相对较高的。

在实验2中，当查询图复杂程度为13(具有13个元组模式的SPARQL查询)时，可以看出RDF- 3X的查询响应速度出现大幅度减慢的情况，说明此刻RDF- 3X的索引表中数据因为太多地进行跨表连接而产生的中间结果冗余情况已经严重影响查询效率。与实验1相同的是，在处理简单图时，RSM的高效性并不明显，但随着图结构复杂程度的提升，RSM的查询响应时间要远低于RDF- 3X与R3F。而GraSS同样是随着查询图的复杂度提升而体现出高效性，但由于其仅对于星形结构进行有效处理，因此其整体进行查询处理的响应时间均要高于RSM，因此，从实验1与实验2中得出的共同结论为，在处理结构复杂的查询图时，RSM的查询响应时间更短，具有更高的查询效率。

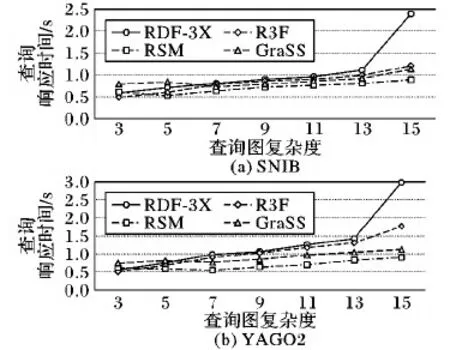
图10 查询响应时间对比实验结果

6 结语

为了提高对于复杂查询图的查询效率，提出了一种基于RDF图切分的子图匹配方法——RSM，提出了相邻谓词结构索引来用于节点的过滤，并为其处理过程设计了相关问题建模与详细举例。在实验部分，本文分别采用了合成数据集SNIB、真实世界数据集YAGO2并与RDF- 3X、R3F、GraSS等主流查询方法进行实验对比以验证RSM的普适性与高效性。实验结果证明，在处理结构复杂的查询图时，RSM的查询响应时间更少，效率更高。在接下来的工作中，将对RSM的可扩展性进行充分研究，将RSM应用在分布式处理平台上，并进一步研究图结构的切分规则，使切分得到的子图结构选择性更加突出。