一种橡胶材料超弹本构等效试验方法

，，

(海军工程大学 a.振动与噪声研究所; b.船舶振动噪声重点实验室，武汉 430033)

国内外对橡胶材料本构模型已有大量研究，主要归为两大类：一类是基于统计热力学的本构模型[1]，如Arruda-Boyce模型和Neo-hookean模型；另一类是基于连续介质力学的维象理论模型，如M-R模型、多项式模型、Ogden模型等[2-4]。完整的橡胶超弹性本构试验应该包含能反映橡胶拉伸、压缩、剪切状态下的力学性能[5]。Treloar[6]最早系统性地研究了橡胶材料的超弹性本构理论，设计等轴和纯剪切本构试验方法，较好地描述了橡胶材料的力学行为。然而，由于橡胶试验比较困难，对设备和试验环境有较高要求，目前，仅简单拉伸试验和压缩试验有国家标准[7]。本文针对船用减振器橡胶部件在实际小变形工作状态，提出利用压缩试验等效替代等轴拉伸的橡胶材料本构试验方法。通过对比橡胶减振器的仿真与试验，分析等效等轴试验描述船用减振器橡胶材料本构模型的合理性。

1 试验基础

基于连续介质力学理论研究橡胶材料本构模型时，将橡胶材料的变形看成是各项同性的超弹性均匀变形，因而将应变能函数表示成变形张量或主伸长率的函数[8]。

W=(I1,I2,I3)

(1)

式中：I与λ之间的关系为

(2)

其中：I1、I2、I3为3个应变不变量；λ1、λ2、λ3为3个主方向上伸长比，伸长比定义为

(3)

其中：L为拉伸后的长度；L0为初始长度；εE为工程应变。橡胶弹性体一般为近似不可压缩材料，即I3可去常数或等于1[8]，对应变能没有影响。对于最一般的类型的均匀应变主应力，真实主应力σTi为[8]

(4)

式中：pe为不可压缩引起的静水压力。式(4)中的各项相减可消去pe，从而计算得到3个方向主应力差值为

真实应力与工程应力的关系为

(6)

式中：σEi为λi方向上的工程应力；σTi、σTj为2个不同方向上的真实应力。对于单轴拉压情况下，式(5)中t2=t3=0，3个方向上的伸长率为

(7)

联立式(5)、(6)、(7)，得到橡胶材料在单轴拉伸下的应力应-变关系为

(8)

式中：σEu为单轴拉伸名义应力(单位长度上的应力)；εEu为名义应变。

橡胶材料在等轴拉伸试验下，式(5)中t2=t3，t1=0，3个方向的主伸长比为

λ1=λ-2，λ2=λ3=λ

(9)

联立式(5)、式(6)和式(9)，得到等轴拉伸下工程应力与应变的关系为

(10)

式中：σEb为橡胶试片等轴拉伸工程应力；εEb为等轴拉伸工程应变。

以应变能函数为基础，表征橡胶超弹性力学行为的超弹性本构模型已有大量研究，如Ogden模型、Mooney-Rivlin模型、Neo-Hookean模型、Yeoh模型、多项式模型等，不同应变条件下，本构模型的拟合精度相差很大，多项式模型的应变能函数为

(11)

式中：Cij为Rivlin系数，定义C00=0，i+j≤N；I1、I2分别为第一和第二Green应变不变量；J为橡胶变形前后体积比；Di决定橡胶材料是否可压缩；N为多项式阶数，橡胶材料为不可压缩材料，J=1，此时：

i+j≤N

(12)

联立式(8)、(10)和(12)，得到单轴和等轴拉伸下，二阶多项式本构方程为

(13)

(14)

采用多目标优化方法[8]，同时拟合单轴拉伸和等轴拉伸试验数据，可得到相应的橡胶本构模型参数。

对不可压缩材料，单轴压缩与等轴拉伸的应力状态相同，其应力-应变对应等价关系为[9]

(15)

式中：σEc、εEc为通过单轴压缩试验计算得到的橡胶材料压缩应力和应变；σEb、εEb为橡胶材料等效等轴拉伸应力和应变。等轴拉伸试验可得到橡胶材料纯的压缩应力状态和精确的试验结果，但是比单轴压缩试验复杂得多，国内此试验条件尚不成熟。因此，本文利用橡胶单轴压缩试验与等轴拉伸试验等价性原理，提出一种以单轴压缩等效代替等轴拉伸的本构试验方法。

2 参数识别

2.1 试验设计

橡胶材料单轴拉伸试验参考GB/T 528—2009进行[10]。橡胶样件为哑铃状，见图1。

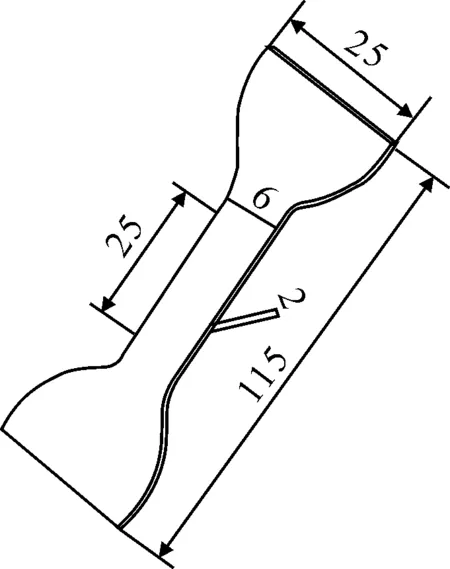
图1 橡胶简单拉伸试验样品

试件厚度为(2.0±0.2) mm，试件长度为(25±0.5) mm，狭窄部分的宽度为(6.0±0.4 mm)。橡胶试件的拉伸试验在SANS拉伸试验机上进行，采用带有传感器的引伸计测量大变形部分伸长量，见图2。

图2 橡胶单轴拉伸试验现场

橡胶材料的单轴拉伸试验目的是为了获得完全的拉伸应力-应变数据，由于填充橡胶存在Mullins效应和迟滞效应[11]，试验中表现为载荷位移不同步。为了减小这种由于材料本身因素的影响而造成的试验误差，采用准静态拉伸速率对橡胶试片进行拉伸试验。单轴拉伸试验所获得的应力-应变关系见图3。

图3 橡胶单轴拉伸应力-应变变化

橡胶弹性体材料的拉伸与压缩应力-应变变化具有很大差别，仅有拉伸试验数据不能很好地确定橡胶材料的本构模型。因此，对减振器橡胶材料本构描述时，必须包含能反映橡胶材料压缩性能的试验数据。

橡胶材料的压缩性能数据通过单轴压缩试验获得。在压缩试验中，由于橡胶试件侧边无法实现自由膨胀，使试件无法实现完全的单向压缩，因而单轴压缩试验数据仅可近似地替代橡胶材料的压缩数据进行橡胶材料本构模型的拟合。这种橡胶材料单轴压缩试验通常用于计算精度要求不高的工程应用中。

单轴压缩试验参考GB/T 7757—93开展[12]。橡胶试件采用如图4所示的圆柱体，其直径为(29.0±0.5)，高度为(12.5±0.5) mm。试件表面光滑平整，上下表面平行。试验在SANS试验机上完成，见图5。试验以10 mm/min的速度压缩试件，再以相同的速度放松试件，连续反复地压缩和放松试件共4次，取最后一次压缩试件的数据为有效数据。单轴压缩试验所获得的应力-应变变化见图6。利用式(15)，得到等效等轴应力-应变变化见图7。

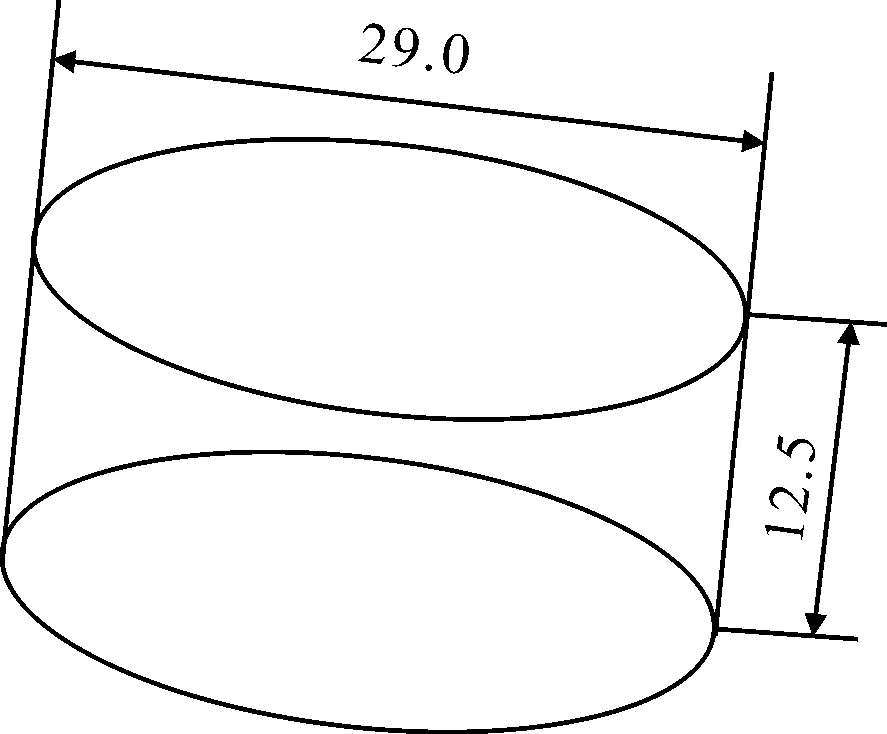
图4 圆柱体单轴压缩试件

图5 橡胶单轴压缩试验现场

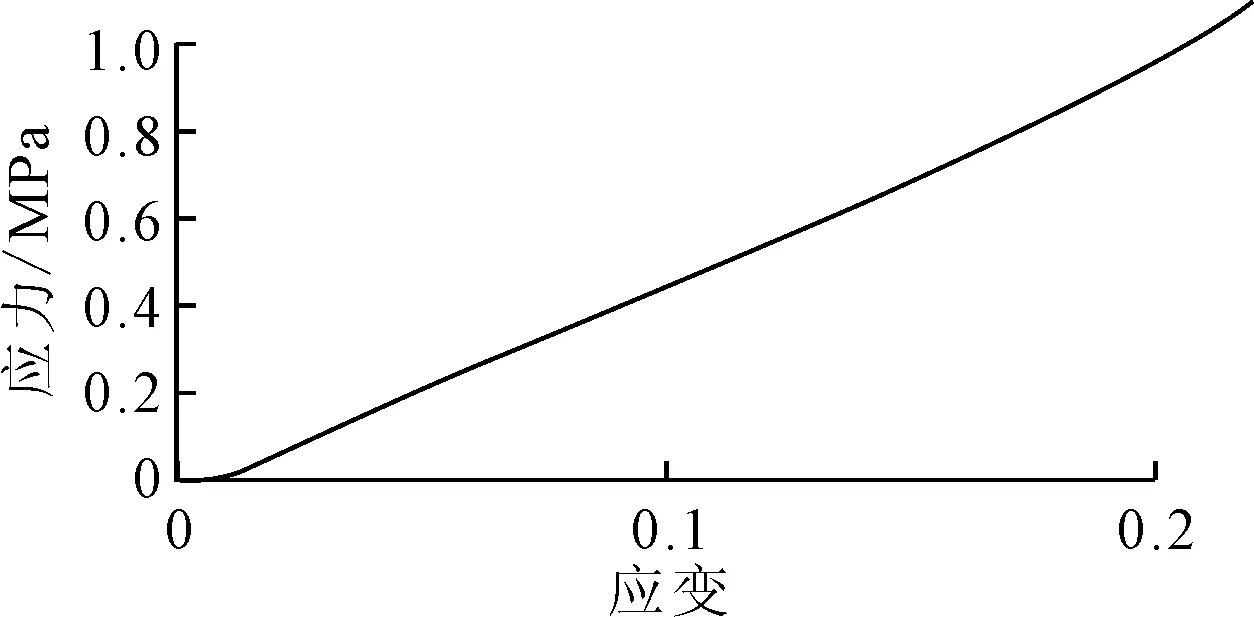
图6 单轴压缩应力-应变变化

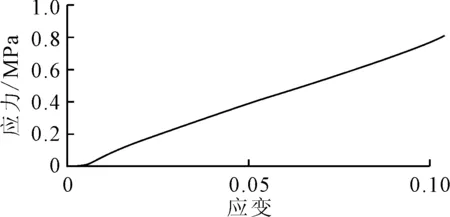
图7 等效等轴拉伸应力-应变变化

2.2 试验结果拟合

利用最小二乘法同时拟合式(13)和式(14)，比较阶次N不同时本构模型与试验数据的拟合程度，发现当N=2时，试验数据与多项式本构模型已经有较高的拟合度，拟合曲线见图8。

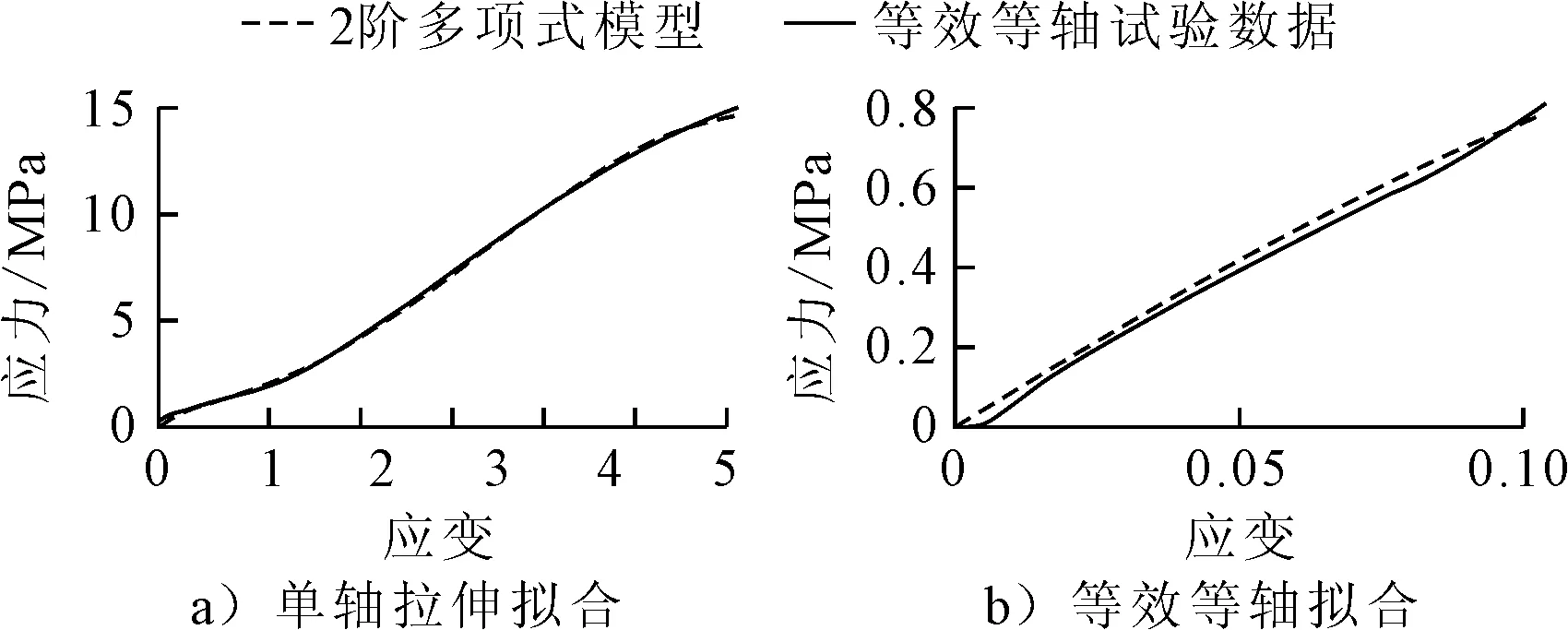
图8 二阶多项式模型与试验数据拟合

如图8所示，二阶多项式模型与单轴拉伸等效等轴拉伸试验曲线拟合接近度较高，与试验数据几乎重合，因而选择二阶多项式模型作为减振器橡胶材料的超弹性本构模型是合理的。拟合结果得到二阶多项式模型的参数如下。

C10=0.278 32 MPa；

C01=0.467 64 MPa；

C20=-5.142 4×10-2MPa；

C11=0.389 94 MPa；

C02=-0.464 08 MPa。

3 有限元模型建立

船用橡胶减振器几何结构复杂，有限元建模较为困难且容易产生计算误差，因此有必要对结构进行适当简化。在利用Pro/E建立几何模型时，将对减振器力学性能影响较小的结构忽略(如包覆在金属表面，防止金属腐蚀的橡胶薄层等)，将几何模型保存为sat格式导入到ABAQUS中，并赋予部件材料属性。

已知船用橡胶减振器的金属件为Q235，材料性能E=210 GPa，μ=0.3。减振器橡胶部件采用C3D8H八节点六面体杂交三维应力单元，支撑轴和限位器等金属部件采用C3D8R非协调八节点六面体单元[13]。

橡胶减振器在生产过程中，橡胶材料与金属件表面经过特殊的硫化处理，其接触面粘接强度甚至比橡胶材料本身强度更高，此外，金属件强度远大于橡胶材料的强度，因此，可将橡胶与金属件接触面定义为绑定约束。建立与实际工况相似的有限元分析模型见图9。

图9 橡胶减振器有限元简化模型

4 试验验证

船用橡胶减振器的静态压缩试验在美国MTS液压试验机上完成，静态测试采用的是力控制，将减振器下端与夹具拧紧，上端用装有力传感器的压头进行压缩加载，见图10。试验开始前，将力值和位移值清零。由于橡胶材料具有迟滞效应和Mullins效应，加载卸载路径不重合，会形成闭合的迟滞环。不能单独以某一条加载或卸载曲线作为衡量橡胶减振器静态性能的指标，需要综合考虑加载和卸载的影响。循环加载、卸载4次，得到迟滞回线见图11。

图10 橡胶减振器静态试验现场

图11 橡胶减振器力-位移的变化

以迟滞中线作为衡量减振器静态性能的指标，得到橡胶减振器的静刚度为786.44 N/mm。有限元模型中，在橡胶减振器上端施加3 000 N向下的轴向力，得到静态仿真结果见图12。

图12 3 000 N垂向压力下仿真结果

从图12可以看出，橡胶减振器的垂向静变形为3.710 mm，计算得到静刚度为808.63 N/mm，与试验结果偏差在3%左右，与实测值较为接近。

船用橡胶减振器垂向力-位移仿真及试验对比见图13。可以看出，橡胶减振器小变形时，有限元计算结果与试验结果几近相同；当静变形逐渐增大到大于4 mm时，仿真结果与试验结果的偏差逐渐增大。分析偏差随垂向位移增大的原因是，有限元模型是将橡胶材料当做理想的超弹性不可压缩材料，而实际橡胶材料除具有超弹性外，还具有粘弹性，橡胶材料变形量增大，蠕变性能和粘弹性对力学性能的影响逐渐突出。

图13 橡胶减振器静态仿真与试验对比

5 结论

根据单轴压缩与等轴拉伸等价关系，提出了以单轴压缩等效代替等轴拉伸的本构试验方法。橡胶减振器仿真和试验结果对比表明，以单轴压缩试验获取橡胶材料本构参数的方法是合理的。与已有橡胶材料本构试验方法相比，本方法对试验设备要求更低，操作更简便，适用于一般橡胶产品的本构模型研究。但由于压缩试件内摩擦力作用，单轴压缩无法获取纯的压缩应力状态和精确的试验结果，因而在精确研究橡胶材料本构模型时，需要进一步对单轴压缩试件内摩擦力特性进行具体分析。