船用离心泵低频振动特性分析

，，，

(武汉理工大学 a.能源与动力工程学院；b.高性能船舶技术教育部重点实验室；c.船舶动力系统运用技术交通行业重点实验室,武汉 430063)

离心泵在正常工作时会引起舰船壳体的低频振动，进而会向流场周围辐射噪声，对舰船的声隐身性能极为不利。目前已有的离心泵振动相关的研究主要针对泵体的振动特性[1-3]，或者针对内部非定常流动诱发的流体激励特性[4-8]，关于离心泵不同工况下的机脚振动特性研究未见报道。由于离心泵内部流场受到结构影响而产生的交变压力脉动是产生振动的主要原因之一，而流固耦合方法适用于解决离心泵的结构与内部非定常流场相互影响的问题[9-12]，因此考虑建立流体域、离心泵、转矩转速传感器、三相异步电动机以及机座的有限元模型，采用流固耦合方法对离心泵在不同工况下0～400 Hz内的机脚振动特性进行分析。

1 计算模型

1.1 模型参数

以IS100-65-315单级单吸卧式离心泵为研究对象，其设计参数见表1。

1.2 三维建模和网格划分

利用Pro/E分别建立离心泵流道计算域、整个泵体(包括蜗壳、叶轮、支架)、转矩转速传感

表1 离心泵设计参数

器、三相异步电动机以及机座的三维模型。为保证计算的可行性，提高运算速度和运算精度，未考虑泵体上的小孔、凸台和倒角。此外，在保证转矩转速传感器和三相异步电动机质量不变的情况下，将其简化成实心圆柱体。机座材料是结构钢，其他结构材料是铸铁，材料的属性见表2。

表2 材料特性参数

利用Workbench的网格自动划分功能实现结构区域网格的生成，网格尺寸d应小于薄板振动波长λ的1/6，即d≤λ/6。经计算，d≤64 mm，因此单元尺寸取为4 mm，满足要求，网格数量为813 681。利用ICEM CFD软件对流体区域进行网格划分，由于流体域的形状比较复杂，因此，采用非结构化四面体网格进行划分。网格尺寸和结构体网格尺寸相同。由于蜗壳隔舌的曲率变化较大，生成的网格质量较差，因此，对该部分进行局部加密，最终流体域的网格总数为2 395 477。计算域网格见图1。

图1 计算域网格

2 数值计算理论

2.1 流体域计算控制方程

对离心泵内部流场采用RANS法进行计算，选用标准k-ε湍流模型，其控制方程组如下[13]。

1)连续方程。

(1)

2)动量方程。

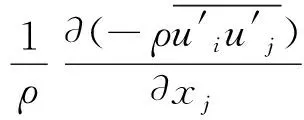
(2)

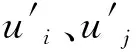
湍动能和湍动能耗散方程分别为

(3)

(4)

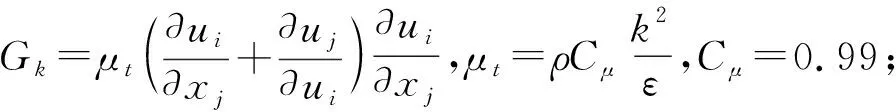
2.2 结构域计算控制方程

离心泵在运行过程中，系统结构每一时刻都承受着流体运动产生的压力，从而引起结构的振动，运用有限元法进行瞬态动力学分析，控制方程为[14]

Mx″+Cx′+Kx=F(t)

(5)

式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；x、x′、x″分别为位移矢量、速度矢量、加速度矢量；F(t)为力矢量。

2.3 数值计算方法

用CFX对流体计算区域进行流场的非定常计算，用Workbench 对结构区域进行瞬态动力学分析。取定常计算结果为其初始条件。在进行流固耦合计算时，分别将结构域的蜗壳、叶片、叶轮前盖板、叶轮后盖板与流体接触的面设置为流固耦合面，对控制方程采用有限体积法进行离散，湍流模型选用标准k-ε模型。进出口条件分别采用压力进口、均速出口，采用标准壁面函数对近壁区进行处理。对流场每隔9°计算一个时间点，即每个计算时间步长为10-3s，叶轮旋转3个周期，一共120个时间步，对3个周期内的流场和结构场的响应进行计算。采用Second Order Backward Euler格式对流场进行瞬时求解，残差收敛目标设置为10-5。流固耦合计算数据传递过程的松弛因子设置为默认值0.75，收敛标准设置为10-3。通过设置不同出口速度对0.60Q～1.40Q5种工况的流动进行模拟。

3 模拟结果

3.1 离心泵外特性和振动特性试验验证

搭建离心泵试验台架，进行清水试验。对离心泵5种工况的扬程和效率进行测量，同时在每个机脚上布置两个测点，对其设计工况下的机脚振动加速度进行测量，测点位置见图2。将数值模拟结果与试验结果进行对比，从而对流固耦合计算结果的可靠性和模型的正确性进行验证。

提取离心泵流固耦合最后一个周期内计算得到的瞬时进、出口压力和转矩，每隔4个时间步长提取1次，并对数据按照式(5)、(6)进行处理，得到各个工况下的扬程与效率，由此绘制出Q-H、Q-η外特性曲线，并与试验所得到的外特性曲线进行对比，见图3。泵扬程和效率的计算式如下。

(6)

(7)

图2 测点布置示意

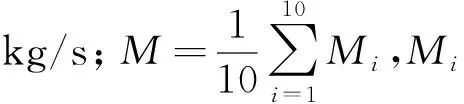
图3 离心泵外特性

由图3可见，流固耦合计算得到的离心泵的外特性曲线与试验得到的趋势基本一致，即扬程随着流量的增大而减小，效率随着流量的增大先增大后减小，且在流量为1.20Q时达到最大。该离心泵比转数为46，属于低比转数泵，扬程、效率曲线也符合低比转数泵的变化趋势。在设计工况附近，扬程的仿真值与试验值误差为5%，其余工况误差均在4%左右，不超过5%。对于效率曲线，在小流量工况时误差最大，为3.20%，其余工况误差均在3%以内。

分别提取离心泵设计工况下1号、3号、6号测点振动加速度的仿真值和试验值，对6个频率点处的振动加速度级进行对比，见表3。

由表3可见，设计工况下机脚的振动加速度级仿真值和实验值相差不大，所有频率点处加速度级差值的平均值为1.97 dB，其中只有3个频率点处的差值超过了3 dB，其余频率点处的平均值为1.33 dB。因此，仿真计算结果基本反映了离心泵机脚在设计工况下的振动特性。从总体来看，流固耦合计算的结果比较可靠，所建立的模型也满足仿真的要求。

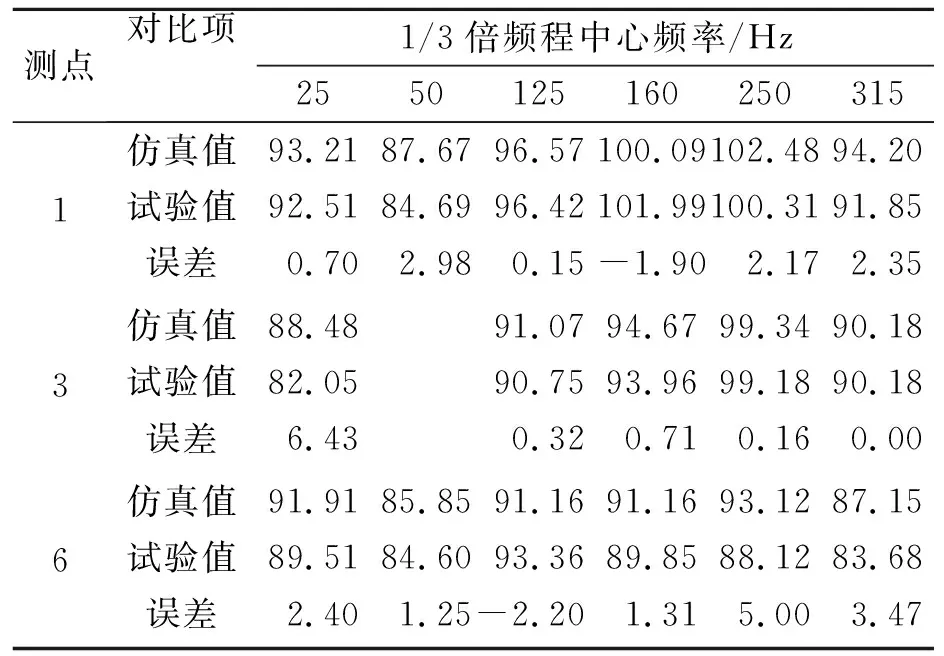
表3 离心泵机脚振动加速度级对比 dB

3.2 离心泵在设计工况下的流场分布

分别对第3个计算周期内T/4、T/2、3T/4、T时刻的流场进行比较，见图4。

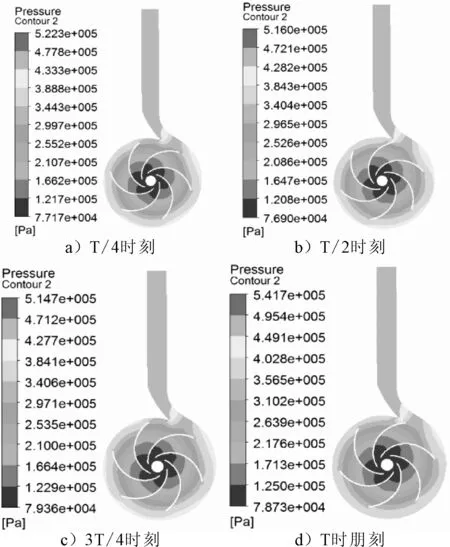
图4 不同时刻的流场压力云图

由图4可见，在这4个时刻，最小压力均出现在叶轮的中心位置，为7.87×104Pa；最大压力均出现在出口延长段，为5.42×105Pa，约为最小压力的6.59倍。叶轮区域的流场压力自叶轮中心沿着半径方向逐渐增大，直到叶梢达到最大，这是因为叶轮在旋转时对流体产生离心力，并且沿着半径逐渐增大，最终在叶梢达到最大。蜗壳区域的流场压力在蜗舌处最小，并且沿着流道逐渐增大，直到蜗壳出口处达到最大，这是因为蜗壳截面面积沿着流道逐渐变大，有扩压的作用。

3.3 离心泵在设计工况下的振动特性

对离心泵在设计工况下的流动进行仿真，得到的加速度云图见图5。

由图5可见，离心泵出口处的振动加速度比机脚处的大，这是因为机脚处施加了约束，出口端没有施加约束，是自由状态。

提取离心泵设计工况下机脚处的加速度仿真值，分别对6个测点最后2个叶轮旋转周期内的数据进行傅里叶变换，得到0～400 Hz范围内的频谱，见图6。

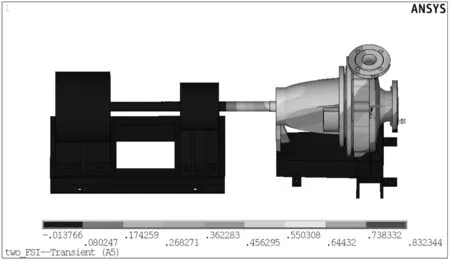
图5 离心泵振动加速度云图

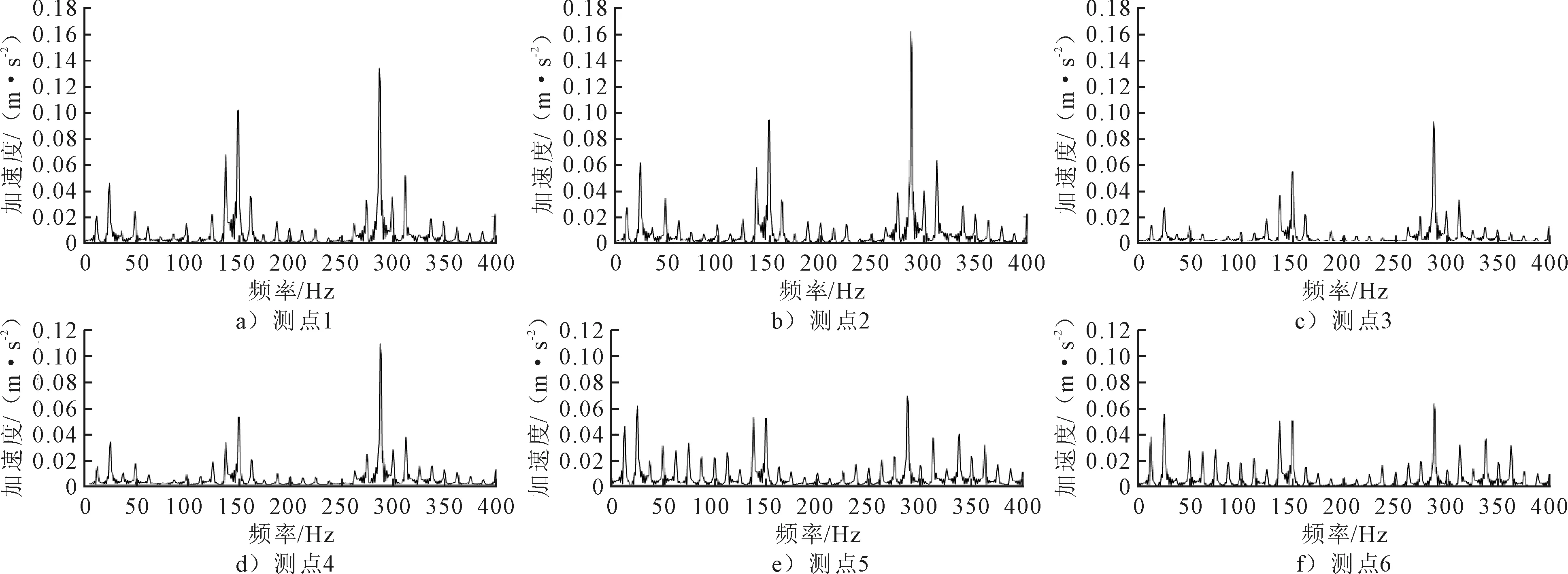
图6 离心泵机脚振动加速度频谱

由图6可见，6个测点均在25.39 Hz出现第1个峰值，离心泵的转速为1 450 r/min，转频为24.17 Hz，说明离心泵在其转频处振动比较强烈。此外，在150.40、287.10 Hz也出现了很明显的峰值。该离心泵有6个叶片，其叶频为145.02 Hz，说明离心泵在叶频和叶频2倍频处也会产生强烈振动，其中1、2、3、4测点在150.40、287.10 Hz处的峰值均比24.17 Hz处高，5、6测点在此频率下的峰值与24.17 Hz处的相差很小，这是由于1、2、3、4测点位于蜗壳一侧，而离心泵在正常工作时旋转的流体会对蜗壳产生周期流体激励力，导致蜗壳处的机脚在叶频和叶频的倍频处产生比较强烈的振动；5、6测点位于远离蜗壳的一侧，没有受到周期流体激励力的直接作用，因此在叶频和叶频2倍频处产生的振动比较小。

从图6还可以看出，测点1与测点2、测点3与测点4、测点5与测点6的频谱图均比较相似，为方便比较，分别对其中8个频率点处的加速度级进行对比，见表4。

由表4可见，相同机脚不同测点处相同频率下的振动加速度级相差很小，所有频率点处差值的平均值小于1.30 dB，其中只有4个频率点处的差值超过了2 dB，最大差值为3.28 dB，其余频率点处的差值皆小于2 dB，其中75%的频率点处的差值小于1.50 dB。因此判断每个机脚可以只提取1个节点的加速度进行振动特性分析；同时，在搭建离心泵机脚振动试验台架时，只需在每个机脚处布置1个测点就可满足要求。

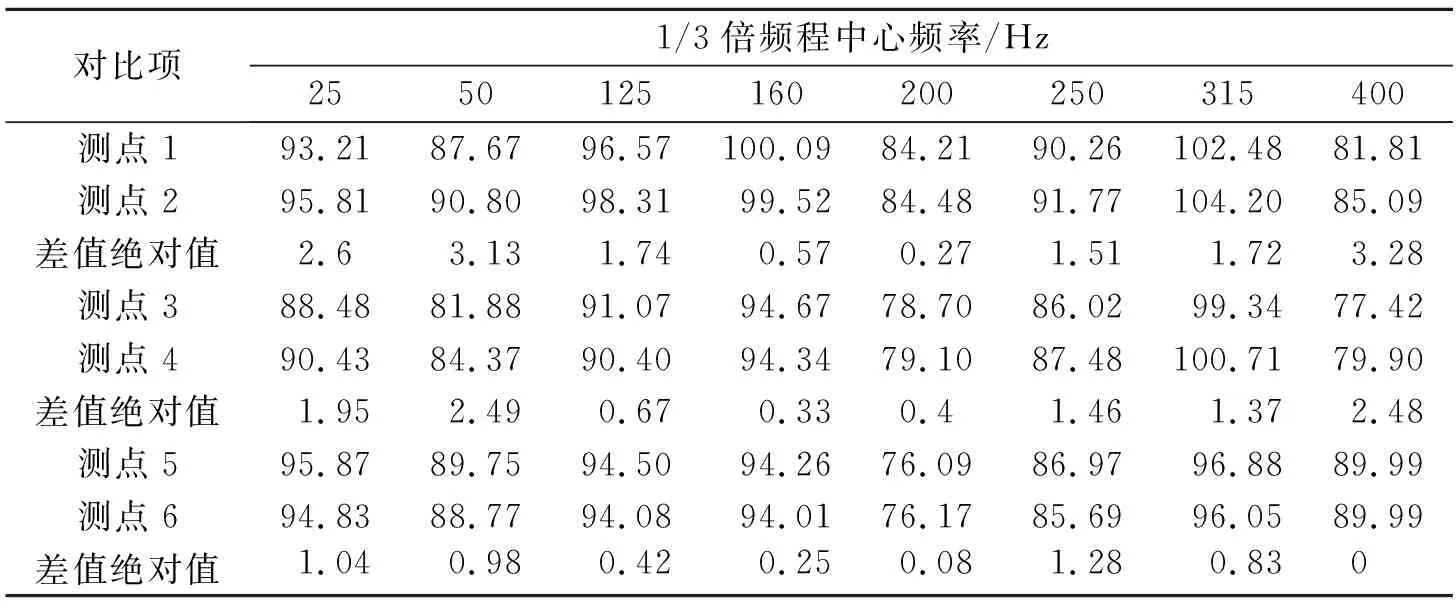
表4 相同机脚不同测点处振动加速度级对比 dB

从图6还可看出，1、2、3、4测点的频谱图较相似，由于1、2测点，3、4测点分别在相同的机脚上，为方便比较，分别对比1、3测点频谱图中11个频率点处的振动加速度级，见图7。

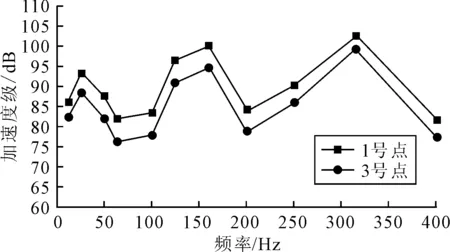
图7 1、3测点处振动加速度级对比

由图7可见，测点1每个频率点的振动加速度级均大于测点3，所有频率点处的差值平均值为4.89 dB，其中最小差值为3.14 dB，最大差值为5.78 dB。测点3所在的机脚靠近离心泵出口侧，测点1所在的机脚远离出口侧，而离心泵蜗壳的截面直径沿着流道逐渐变大，在出口达到最大，有扩压的作用，因此水在蜗壳内流动时动能转化为压力能，流速减小，水压增大，从而水的动量减小，测点3所在的机脚受到的流体激励力小于测点1所在的机脚，最终导致测点1的振动比测点3强烈。

3.4 离心泵在不同工况下的振动特性

分别对0.60Q、0.80Q、1.20Q、1.40Q流量时的流动进行流固耦合模拟。提取各工况下测点1、3、5的振动加速度数据并进行傅里叶变换，3个峰值频率(25.39、150.40、287.10 Hz)处的振动加速度级，见图8。

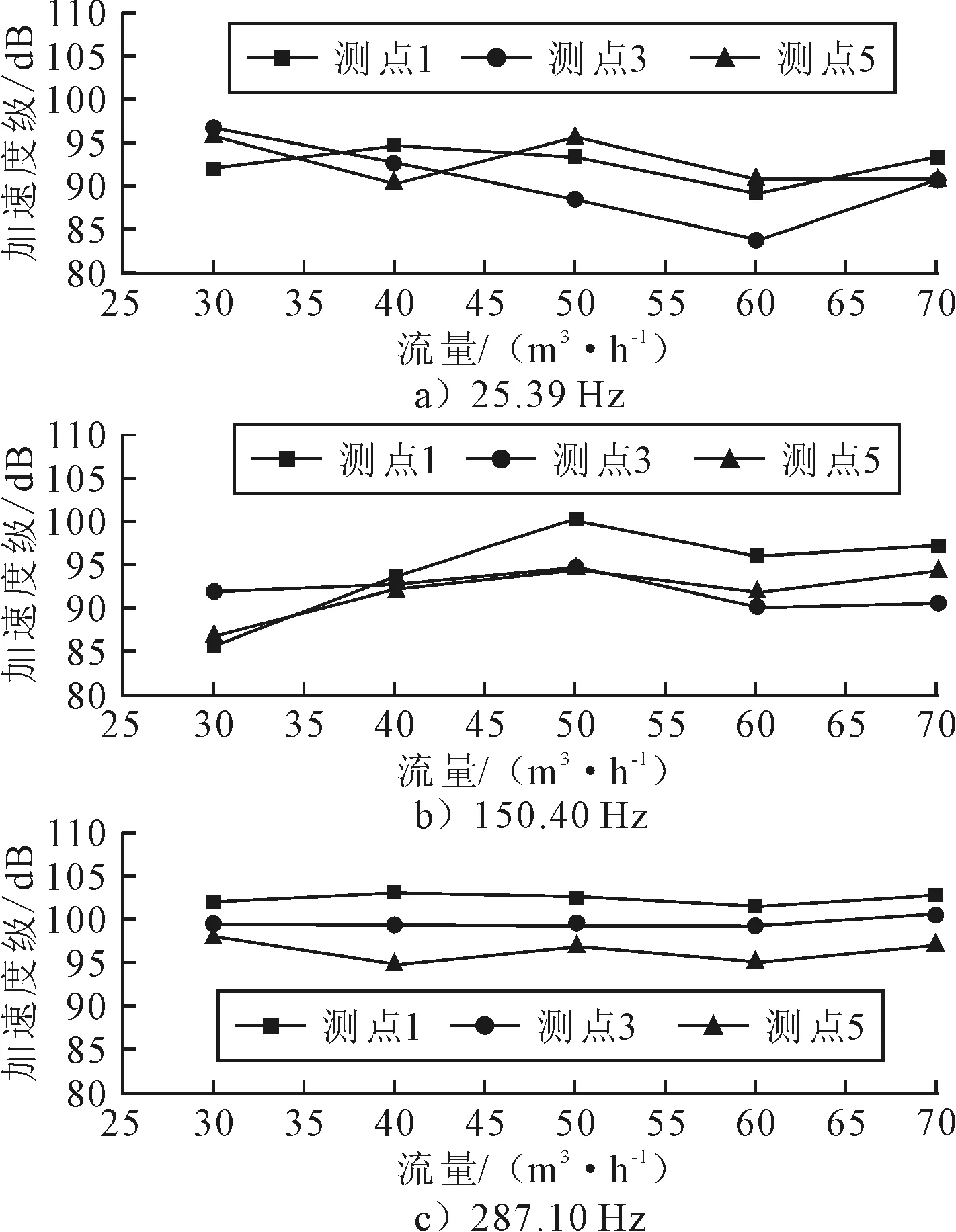
图8 不同工况在峰值频率处的机脚加速度级对比

由图8可见，c)图中的曲线比a)、b)图中的平稳，其中25.39、150.40 Hz2个频率点处加速度级变化量的平均值分别为3.95、3.34 dB，而287.10 Hz处的为1.18 dB，说明测点1、3、5在25.39、150.40 Hz处的振动加速度级随着工况的变化而产生的变化比287.10 Hz处大。此外，a)、b)、c)中的曲线均在1.20Q时出现低谷，说明离心泵3个机脚的振动在1.20Q工况时呈现下降趋势，结合前述Q-η曲线显示离心泵在该工况下效率最高，因此建议同类型的离心泵工作时尽量采用1.20Q工况。

4 结论

1)在0～400 Hz内，离心泵的机脚在转频、叶频以及叶频的2倍频处会产生强烈的振动，而且蜗壳一侧的机脚在叶频和叶频两倍频处的振动比转频处的强烈，建议在实际安装中针对转频、叶频以及叶频2倍频处的振动采取减振措施。

2)在对离心泵机脚进行振动特性分析时，每个机脚只需提取1个节点的振动数据就可满足分析要求，同时在对离心泵机脚的振动进行测试时，只需在每个机脚布置1个测点。

3)对于蜗壳处的机脚，由于蜗壳流道的扩压作用，远离离心泵出口侧的机脚振动加速度级比靠近出口侧的机脚 大4.89 dB，实际安装中应着重对远离出口侧的机脚采取减振措施。

4)离心泵在转频、叶频处的振动随着不同工况而产生的变化比叶频2倍频处大，且3个机脚在转频、叶频以及叶频2倍频处的振动在1.20Q工况时均呈下降趋势，建议同类型的离心泵在工作时尽量采用1.20Q工况。

仿真计算时只考虑了转矩转速传感器和三相异步电机的重力对离心泵机脚振动特性的影响，未能模拟实际工作状况。因此，下一步应开展能精准模拟转矩转速传感器和三相异步电机正常工作的建模方法的研究。