DBD等离子体非定常激励下的平板流场结构分布研究

吴延龙，马玉伟，俞建阳

（1.中国空间技术研究院，北京 100094； 2.北京空间飞行器总体设计部，北京 100094；3.哈尔滨工业大学 航天学院，哈尔滨 150001）

0 引言

等离子体流动控制技术具有广阔发展空间和应用前景。2004年，美国国防部将等离子体流动控制技术列入面向空军未来发展的重要领域[6]，希望通过研究掌握等离子体的电离流动过程，奠定实现飞行器性能革命的科学基础。2009年，美国航空航天学会将以等离子体流动控制为代表的主动流动控制技术列为十大航空前沿技术之一。同年，欧洲制定了PLASMAERO（PLASM as for AERO Dynamic Control）合作研究计划。

随着主动流动控制的快速发展，介质阻挡放电（dielectric barrier discharge, DBD）等离子体流动控制技术作为一种新型主动流动控制技术[1]，在全球范围内引起关注。已有研究表明，DBD等离子体流动控制技术能有效减小湍流边界层阻力并抑制边界层分离[2]，对抑制翼型失速[3]、提高涡轮效率[4]、减小气动噪声[5]等都有较好的控制效果。

国内外对于等离子体非定常激励的流动控制已经展开广泛研究，但是对于等离子体非定常激励与流场内部的相互作用还缺少详细的研究工作。而对等离子体流动控制过程机理的把握是将其付诸应用的前提。本文利用大涡模拟（LES）方法，通过对DBD等离子体非定常激励作用下的流场进行数值模拟研究，分析附面层内的流动状况，进一步总结和揭示等离子体流动控制的规律和机理。

1 数值方法

1.1 等离子体简化模型

等离子体激励器由高压电源、绝缘介质以及一对金属电极（分别裸露于空气中和植入绝缘介质中）构成。当电极两端施加了足够强度的电压后，激励器周围的空气会被弱电离出带电粒子。带电粒子在电场力的作用下定向移动并同周围的中性气体分子进行动量交换，从而产生诱导流动。等离子体激励器及其附近电场线性分布如图1所示。

动量注入效应是DBD等离子体对流动作用比较确定的作用机理，国内外的学者对此提出了一些相应的简化模型，其基本思想是：将粒子碰撞导致的动量传递效应简化为作用于流体的电场力，并以体积力源项的形式耦合到动量方程中。Orlov[7]、Shyy[8]、Suzen[9]根据不同的简化条件和实验结果分别提出了各自的简化模型，其他学者也在这些模型基础上进行了大量的研究工作。Rizzetta[10]基于Shyy提出的简化模型对等离子体对湍流附面层的流动控制进行了数值研究。毛枚良等[11]利用简化模型，对NACA0015翼型进行了数值研究，探讨了大气压辉光放电下等离子体对边界层流动的影响。陈浮等[12]基于3种不同简化模型，对比研究了5 kV激励电压作用下的诱导流场，分析了各模型的优缺点。已有的成果表明：简化模型已被广泛用于等离子体流动控制的研究，并可实现对等离子体激励器动态特性的有效捕捉。

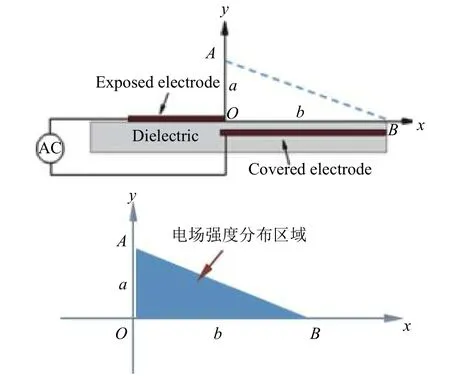
图1 等离子体激励器及其附近电场线性分布Fig.1 The plasma actuator and the distribution of electric strength around it

本文采用Shyy等人提出的唯象模型开展相应的非定常等离子体流动控制数值研究。该模型建立在线性化电场以及等离子体密度恒定假设的基础上，由

可获得激励器附近的电场分布。式(1)中：E=φ/L，φ为电势，L为2个电极在x方向上的间距；E0为图1所示Oxy坐标系中坐标原点的电场强度。E随x、y的递增而线性递减，当电场强度小于临界值Eb时，不再有等离子产生。由K1=（E0-Eb）/b和K2=（E0-Eb）/a可得电场力

其中：ρc为等离子体电荷密度；ec为元电荷。将电场力F以源项S的形式耦合到N-S方程中，从而实现对DBD等离子体非定常激励作用下的流场进行数值模拟。

1.2 大涡模拟方法

目前一般采用雷诺平均（RNS）、大涡模拟（LES）、直接数值模拟（DNS）等方法对具有确定边界条件流动问题进行求解。其中：DNS能够获得最精细的高精度、高分辨率流场信息，但其受到硬件条件的制约未能获得广泛的运用；RNS受限于湍流模型的准确性、普适性，导致其计算精度较低，对流场细节的反映存在不可避免的缺陷，无法满足一些精度要求较高的研究需求；LES可以在保证较低计算成本的前提下充分描绘流场的整体特征，同时最大程度刻画流场的细节。

本文采用LES方法对DBD等离子体对流场的非定常作用进行三维求解，亚格子模型采用WALE模型。引入电场力F后的N-S方程的通量形式为

式中：ρ为流体密度；v为流体的运动速度；g为重力加速度；f(t)为非定常激励函数。

1.3 物理模型及计算初边界条件

本文对等离子体非定常激励下的平板流动进行数值仿真研究，仿真时采用如图1所示的等离子体激励器的布置形式，激励器的参数为b=3 mm、a=1.5 mm[13]，定义计算域入口（右边界）的自由来流速度U∞=10 m/s、边界层厚度δ=5 mm，取裸露电极后缘与平板的交点为坐标原点。计算域为25b（x向）×10b（y向）×4b（z向）（如图2 所示），为保证计算精度，壁面第1层网格为0.02 mm，设置计算域侧面为周期性边界条件。

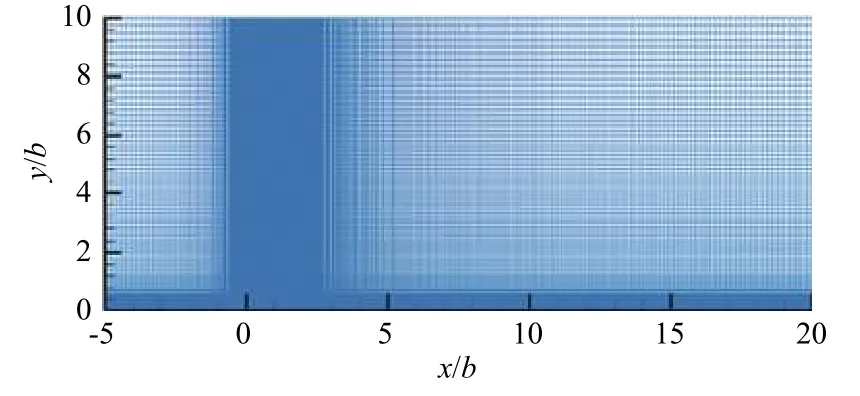
图2 平板流动计算域Fig.2 Computational domain of the flat plane

在等离子体非定常激励的计算过程中，定义等离子体的激励强度为量纲为1的参数Dc，用以表征电场力和惯性力之比，

定义占空因子Dtc=Td/T，其中Td表示1个周期T内等离子体的作用时间。

2 结果分析

图3为Dc=30、Dtc=0.4、激励频率 1500 Hz的等离子体非定常作用下的流场瞬时速度分布（U/U∞）。可以看出，等离子体在近壁区附近形成周期性的诱导速度。该诱导速度在壁面摩擦以及流体黏性的作用下，随着向下游移动不断减弱。当形成周期性的稳定流场时，计算流场的时均速度分布，获得如图3中沿流向S1～S6（x依次为-2.0b、0.5b、2.0b、5.0b、7.0b、10.0b）位置处的有/无等离子体作用下的流场速度对比曲线（见图4）。由图4可以看出，非定常等离子体对流场的作用时均结果表现为从等离子体作用点形成向下游发展的壁面射流。近壁区的诱导速度呈反C形分布，在S2位置处诱导流动的速度达到了最大值1.8U，在S5之后最大诱导速度基本保持不变，但其所在y向位置向y轴的正方向移动。

图3 等离子体作用下的流场瞬时速度分布Fig.3 Contour of the flow speed under plasma action

图4 沿流向不同位置处的速度分布对比Fig.4 Streamwise velocity profiles at different locations

图5分别给出了不同激励强度（Dc=25、30、35、50）的非定常等离子体作用下的稳定流场，可以明显观察到周期性的涡量（ω∗=ωz·δ/U∞）以及速度团（µ∗=U/U∞）的存在。特别是在Dc=50时，近壁区内存在着以正负涡量构成的涡对结构在来流的作用下向下游迁移，且涡对的强度随着向下游移动逐渐减弱，涡对中负涡量同壁面附近的涡量层逐渐融合，而正涡量在向下游运动的过程中逐渐衰减，表现在瞬时速度的分布上为集中的高速度群的不断扩散。

图5 不同激励强度作用下的稳定涡量场和速度场Fig.5 Vorticity and velocity contours for different intensities of actuation

借助湍流动能的概念来探讨因等离子体引起的流场速度脉动的分布规律。图6给出了不同激励强度作用、不同流向位置（x=0、x=0.5b、x=b、x=2b、x=4b、x=6b）处的湍动能分布对比。由图可见，壁面附近流场在流向位置x=0之后存在着明显的湍动能分布。值得注意的是，在x=0.5b的位置附近，湍动能达到最大值，其分布趋势与图5中速度的分布趋势一致。这是由于湍动能的大小跟流体的速度密切相关，因而两者有相同的分布趋势。而在等离子体激励器的下游，上游的诱导速度在流动中不断损耗不能长期维持，湍动能在不断消耗而无生成。因此，随着向下游移动，湍动能逐渐减小并远离壁面。对于不同激励强度，在相同流向位置处，湍动能的大小随激励强度的增加而增大。

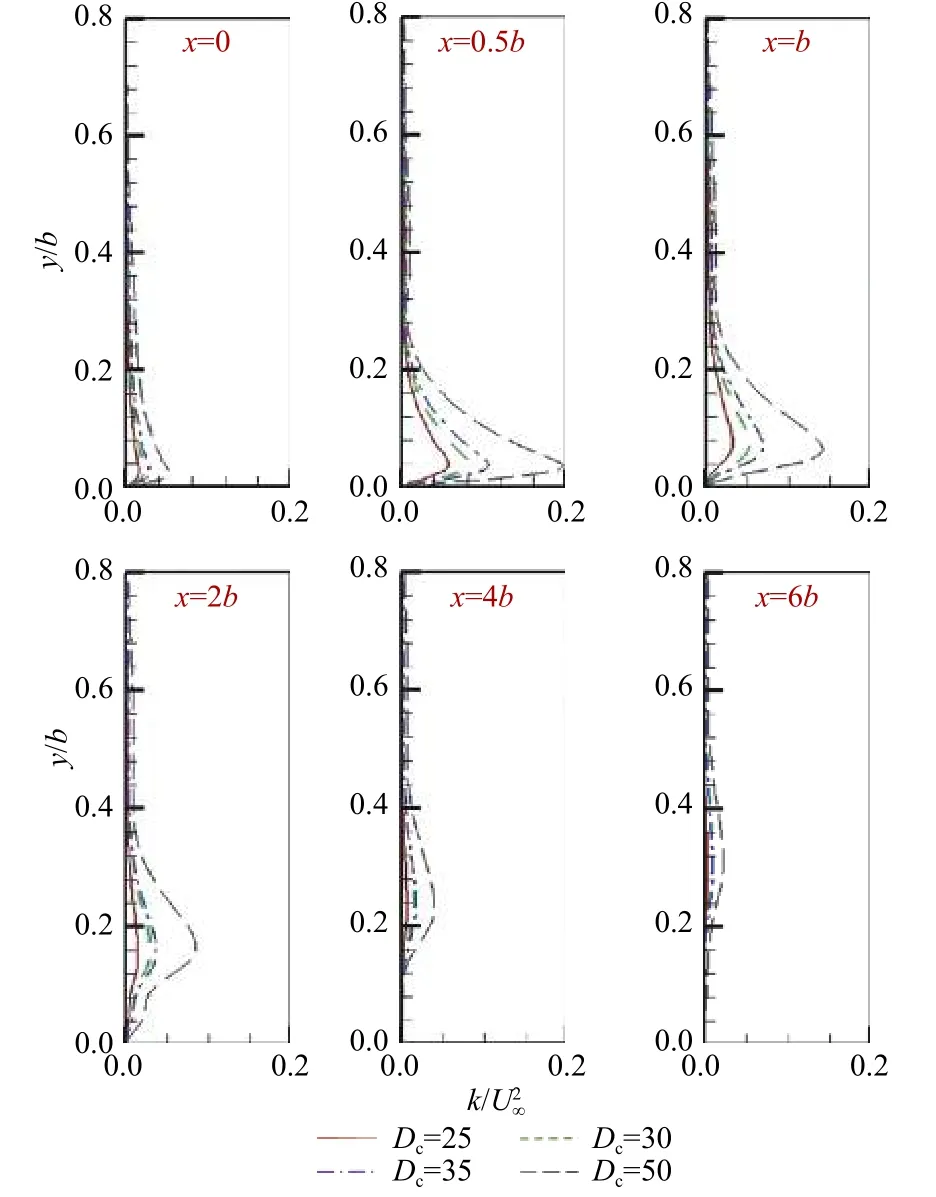
图6 不同流向位置处的k/U∞2分布对比Fig.6 Mean turbulent kinetic energy profiles at different locations

图7所示为不同流向位置处雷诺应力沿高度方向的分布。雷诺应力反映了对应流体微团由于跳动引起的界面两侧的动量交换。跳动是由大大小小的旋涡（湍流脉动）引起的。雷诺应力的分布与不同方向速度的梯度密切相关，在激励器附近诱导速度有向下的速度增量导致了如图7中x=0和x=0.5b位置处的雷诺应力分布。在x=b以后，雷诺应力均为正值分布，其最大值的分布位置在x=2b附近，与速度和湍动能的最大值位置不同。对于不同的激励强度，雷诺应力的分布趋势是相同的。

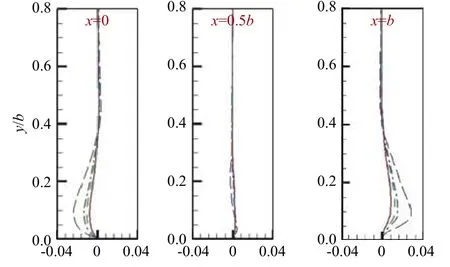
图7 不同流向位置处的雷诺应力分布对比Fig.7 Mean Reynolds stress profiles at different locations

定义涡对中正涡量的最大值及其所在位置为其涡核高度（H）和涡核核心。图8和图9分别给出了流场中正涡量核心的涡量值及相应的涡核高度。从处理的结果可知，增大等离子体的激励强度可以明显增加等离子体激励器对周围流场的诱导作用，其诱导涡量的强度能够在流动黏性和摩擦的作用中较好保持，对流场的影响范围亦随之增加。

图8 不同激励强度下的涡量衰减Fig.8 The vorticity of vortex pair for different actuation strength

图9 不同激励强度下的涡核高度Fig.9 The spatial trajectories of the positive vortex for different actuation strength

为进一步探讨等离子体诱导速度与激励强度的关系，对不同激励强度下的仿真结果进行处理，获取x=0.5b位置处的最大诱导速度UDBD与激励强度Dc的关系如图10所示。通过拟合可以得到UDBD=exp(0.516 8×lnDc+0.960 2)，即等离子体对于流场的最大诱导速度与等离子体的激励强度间满足指数增长关系，随着激励强度的增强，最大诱导速度也逐渐增大。

图10 最大诱导速度与激励强度的拟合曲线（x=0.5b）Fig.10 Relationship between the actuation strength and the maximum induced velocity(x=0.5b)

3 结论

鉴于DBD等离子体激励器在诸多流动中较好的控制效果，本文采用大涡模拟方法将非定常DBD等离子体模型与N-S控制方程耦合建立了DBD等离子体作用下的流动求解模型，实现对DBD等离子体激励器作用下的流动控制过程的仿真计算，探讨了DBD等离子体作用下的平板流动的流场结构特点。通过上述研究工作，获得了以下主要研究成果和结论：

1）在等离子体激励器作用下，流场近壁区诱导形成了一系列的正负涡对结构，涡对的产生进一步促进了近壁区内流体与主流流体的能量交换。诱导涡对有效地提高了附面层内的流体速度，但其在向下游迁移的过程中不断地远离壁面，对流动的控制作用不断减弱。

2）在等离子体作用点下游0.5b的位置存在着最大的诱导速度UDBD，其与激励强度Dc满足关系UDBD=exp(0.516 8×lnDc+0.960 2)。

上述结论可为进一步揭示DBD等离子体激励器作用过程中所发生现象的内在机理，进而为DBD等离子体流动控制技术在工程实际中的应用提供理论支持。