矿渣粉磨健康状态识别模型及系统设计

代 风， 纪杨建， 万安平， 张 真

(浙江大学机械与工程学院 杭州，310027)

引 言

矿渣粉磨是一种将建材、化工及钢铁等行业生产剩余的大颗粒矿渣物料研磨成细微颗粒的重型高能耗设备，又称立磨。矿渣物料经研磨得到的微粉通常作为水泥生产的原料，可实现废渣的再利用[1]。但是立磨系统工艺复杂、工作环境恶劣，高负荷运行时常会出现系统故障，导致生产率下降、设备维修及停产成本激增[2-3]。因此，迫切需要对立磨系统进行运行状态监控，识别和预测立磨系统的健康状态[4-5]。

近年来，国内外学者对复杂装备的健康状态预测技术进行了较为深入的研究。基于物理模型的方法为其常用方法，采用数学模型描述直接或间接影响相关组件健康状态的物理过程[6]。文献[7]基于模型的重型燃气轮机气路故障诊断方法，建立了重型燃气轮机气路故障诊断系统。文献[8]针对精确度和有效剩余寿命的置信空间等问题讨论了预测在实际应用中的情况。文献[9]将物理模型应用于设备状态的预测，结合了基于裂缝发育规律的故障强度模型，可用于对设备的有效剩余寿命预测。文献[10]在对模型正常工作情况和退化状态进行仿真的基础上搜集了一系列数据，建立了一个集成的预测模型。可见，基于失效物理的方法虽然可以获得较为精确的预测结果，但为了建立完备的失效物理模型，需要对设备进行停机检查，而这是工程生产中需要避免的。

文献[11]基于状态外推的方法，根据预测设备运行状态的进一步发展与失效阈值进行比较，来预测设备的剩余寿命分布。文献[12]分析了性能退化量对突发失效的失效阈值影响，建立了基于变失效阈值的竞争失效可靠性模型。文献[13]以轴承振动信号的功率谱密度为特征变量，失效阈值为假设值，通过滚动轴承实验数据验证了其有效性。文献[14]根据拟合的分布参数函数预测将来的失效时间分布，得到了一种基于伪失效时间数据的可靠性分析方法。以上研究大多需要预设失效阈值，还需要对设备发展趋势进行预测。

基于统计分析的寿命预测模型是通过大量的寿命试验来分析机械设备的失效情况，综合各种可能的因素，应用数理统计分析的方法，选择恰当的寿命分布模型，建立以可靠性为基础的统计学公式，获得产品寿命的特征分布[15-16]。文献[17]建立符合非线性Wiener过程描述的设备退化模型，利用先验数据实现对设备实时剩余寿命评估。文献[18]提出了一种融合随机退化过程与失效率建模的设备剩余寿命预测方法。分析上述文献可知，得到设备失效概率的函数需要大量同类设备的历史数据。随着信息化和自动化技术的发展，特别是传感器、数据采集装置在复杂产品上的广泛应用，立磨设备的生命周期数据能被实时地记录，具有大数据 4V的特点。其中，运行过程中的数据增长幅度最大，这些数据已经在时间和空间上隐含了产品服役性能特点和演化特征[19]。大数据分析侧重通过分布式或并行算法提高现有数据挖掘方法对海量数据的处理效率，在许多领域开展了有益的探索和初步应用[20-22]。

笔者提出一种基于数据挖掘的立磨系统健康状态识别模型，通过健康状态评估指标确定、健康状态聚类分析最终比对获取立磨系统的即时及预测健康状态评估。此外，通过应用系统开发实现了识别模型的工程应用验证。

1 健康状态识别模型

1.1 健康状态判断指标确定模型

健康状态判断指标是指能够表征系统健康状态的一系列设备运行参数。壳体振动是反映立磨系统平稳运行和良好生产状态的重要因素，是系统实际运行中重点监控的参数指标。立磨系统的健康运行状态可描述为：一定时间周期内，在额定产量不变的前提下，立磨壳体振动幅度保持在合理范围的一个持续状态。

壳体振动幅度是一个监控变量，需要通过调节其他可调参数实现振动幅度大小的稳定。立磨系统是一个高耦合系统，振动会随着多种因素的改变而变化。为了找到对振动影响较大的关键参数，确定与稳定状态相关的特征，需要进行特征选择。常见的特征选择方法包括随机lasso、岭回归、随机森林、稳定性选择和递归特征消除等。这些方法有各自的优缺点：岭回归及随机lasso需要调整参数，实现对模型系数的稀疏性进行控制；随机森林计算中常出现过拟合问题；稳定性选择是基于二次抽样的，不同的抽样效果得到的结果不同；递归特征消除的稳定性则依赖于底层模型的选择。

为了优化稳定状态判断结果的准确性，笔者综合上述5种算法，避免了单一方法的局限和缺点。其原理是通过求解输入和输出之间的关系，分别使用5种方法获取稳定特征，然后对每个特征的重要性予以打分，按照得分结果对特征的重要度进行评估，特征筛选过程模型如图1所示。最终获得关键参数及数值范围共同构成系统健康运行状态特征。

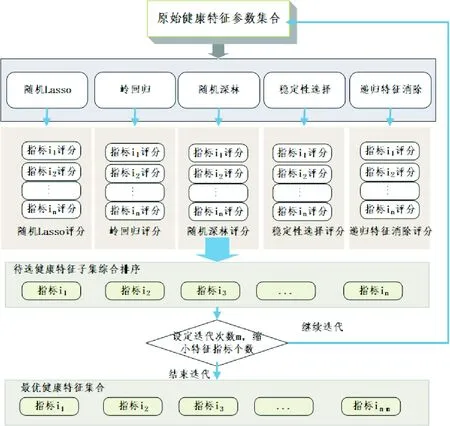
图1 关键健康特征挖掘过程模型Fig.1 Key feature mining process model

1.2 健康运行状态的工况聚类分析模型

健康运行状态的工况聚类是指在确定健康状态判定指标的基础上，对样本数据的不同工况模式进行聚类分析，获取可能的工况模式类别。首先，根据参数数值分布及实际生产经验，对样本数据进行预处理筛选，将筛选结果作为聚类计算的输入；其次，采用K均值法获取数据集中的工况簇，分别找到数据集中的K个簇的质心，并把数据集中的点分配给与其距离最近的质心，认定该点为对应质心所属的类别，K的取值需要根据运行结果不断调整迭代法；最后，在确定工况聚类的类别后，需要对样本数据中所有运行工况进行标记，建立健康工况模式库。健康工况模式库的建设过程模型如图2所示。

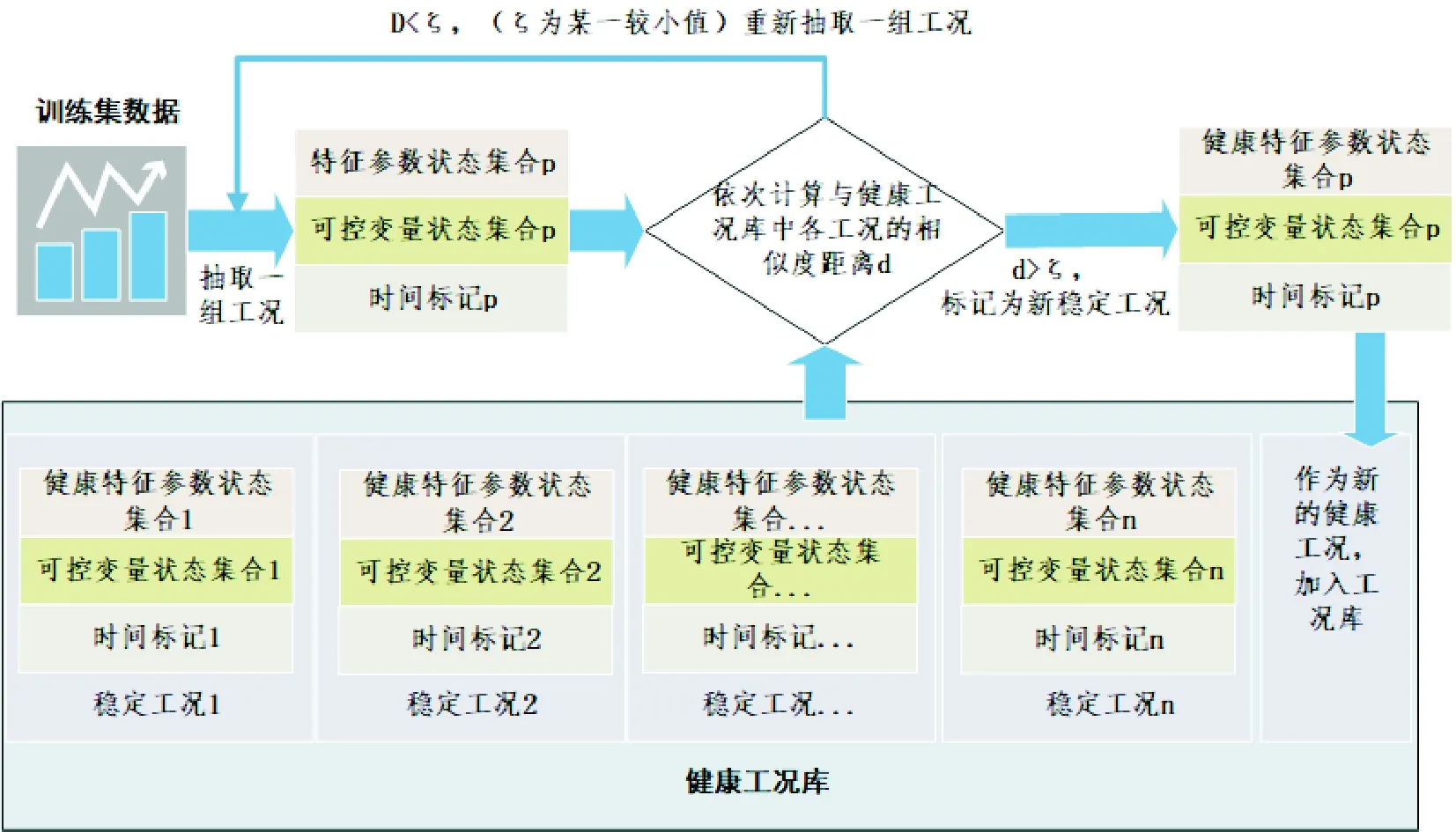
图2 健康工况模式库建立过程模型Fig.2 Establishing process model of stable working condition library

首先，抽取一组工况数据集，它包含一组可控变量状态集合、一组健康特征参数集合以及时间标记；然后，分别计算每组工况中参数构成的向量与工况库中已有工况向量的相似度距离。若存在距离小于一个较小值ζ，则认为工况库中已存，不再重复记录；否则，将该工况存入健康工况库。需要说明的是，在实际工程应用中健康工况模式库并非固定不变，需要定期对其进行训练更新。

1.3 实时健康状态评估模型

实时健康状态评估是指基于系统实时运行数据与健康工况模式库比对，实时获取健康状态评估的过程。在实际生产过程中并非直接利用瞬态单点数据作为判断依据，而是对运行数据进行空值、异常值清洗，再进行一定周期的均值计算后评估。针对已确定的健康特征指标，分别计算每个参数实时运行数据在采集窗口时间内的均值、方差和异常值出现次数，把得到的结果作为稳定工况判断的特征变量，并与健康工况模式库中的状态进行比对。实时健康状态评估的流程如图3所示，其步骤如下。

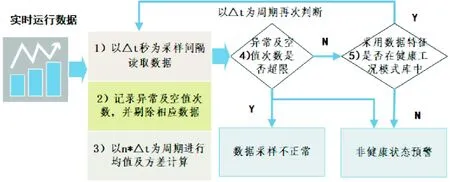
图3 实时健康状态评估过程模型Fig.3 Real-time data healthy-state judgment data acquisition process

1) 以某时刻T为起始时间，按照Δt为采样间隔(基于生产现场控制计算机性能)，分别采集健康特征指标各参数的实时运行数据。

2) 针对各参数的采样数据进行空值及异常值清洗处理，分别记录异常值及空值次数。每次技术累加。

3) 分别对各参数空值及异常值处理后的数据以n*Δt为周期进行均值及方差计算(n为采样窗口周期的倍数)。

4) 判断各参数在判定周期内空值及异常值出现的次数(异常值是指超过健康特征参数临界范围的数值)，如果大于预设定的计数阈值，则认定当前工况异常或不适于健康状态即时评估，需提醒现场生产人员检查。

5) 分别以各参数在取数周期内的均值和方差作为即时工况特征，与健康工况模式库进行比对判断。当出现不符合健康工况状态或与非健康工况状态相似时，需提醒现场生产人员检查。

1.4 健康状态预测评估模型

健康状态预测评估是指在实时运行数据评估的基础上，对其未来一定周期内的运行工况进行预测，并评估其健康状态。这里首先明确一个概念——平稳序列：对于一个序列{X(t)}，如果数值在某一有限范围内波动，序列有常数的均值和常数方差，并且延迟k期的序列变量的自协方差和自相关系数是相等的，则该序列为平稳序列；反之为非平稳序列。

由于立磨系统工况序列属于非平稳序列，因此笔者采用ARIMA进行时间序列建模。ARIMA的实质是在自回归移动平均模型(auto-regressive moving average model，简称ARMAM)上添加差分运算，如式(1)所示

xt=φ0+φ1xt-1+φ2xt-2++φpxt-p+

εt-θ1εt-1-θ2εt-2-...-θqεt-q

(1)

该模型认为在t时刻的变量x的值为前p期的x取值和前q期的干扰ε的多元线性函数。误差项为当前的随机干扰εt，为零均值白噪声序列。

基于实时运行数据的历史时间序列可以预测未来某一时刻t的系统运行工况，进而实现其运行健康状态的预测评估。

2 系统组成及分析

笔者基于健康状态识别模型，设计并开发了一套立磨健康状态识别系统，其总体结构框架如图4所示。系统主要包括数据前处理、健康状态评估指标挖掘、健康状态聚类分析、实时健康状态评估以及健康状态预测等5个功能模块。

数据前处理模块主要实现对样本数据的预处理功能。模块首先实现对异常值、空值进行清洗，然后进行离散化和归一化加工，最终获取便于挖掘分析的完整数据集。

健康状态评估指标挖掘模块用于确定可以判定系统稳定状态的参数种类及其数值边界。采用健康状态判断指标确定模型，对工况数据进行挖掘分析，然后依次得到表征系统健康状态的关键参数。

健康状态聚类分析模块实现对系统运行数据的分类挖掘，获取稳定特征参数不同时间窗口数值组成的工况簇，最终形成可识别的运行状态工况模式库。采用健康运行状态的工况聚类分析模型，得到各个工况簇特点及工况中的状态分布情况，定义历史工况中的运行状态类别，最后对各工况所属的状态进行类别标注和筛选，形成工况模式库。

实时健康状态评估模块实现对系统即时运行健康状态评估判断。采用实时健康状态评估模型对稳定特征指标的实时运行数据进行分析，获取是否健康运行的评估判断。

健康状态预测模块利用对实时运行数据的分析，实现对未来一定周期内系统运行健康状态的预测。其原理是利用健康状态预测评估模型进行健康预测模型训练，实现系统健康状态的预测。

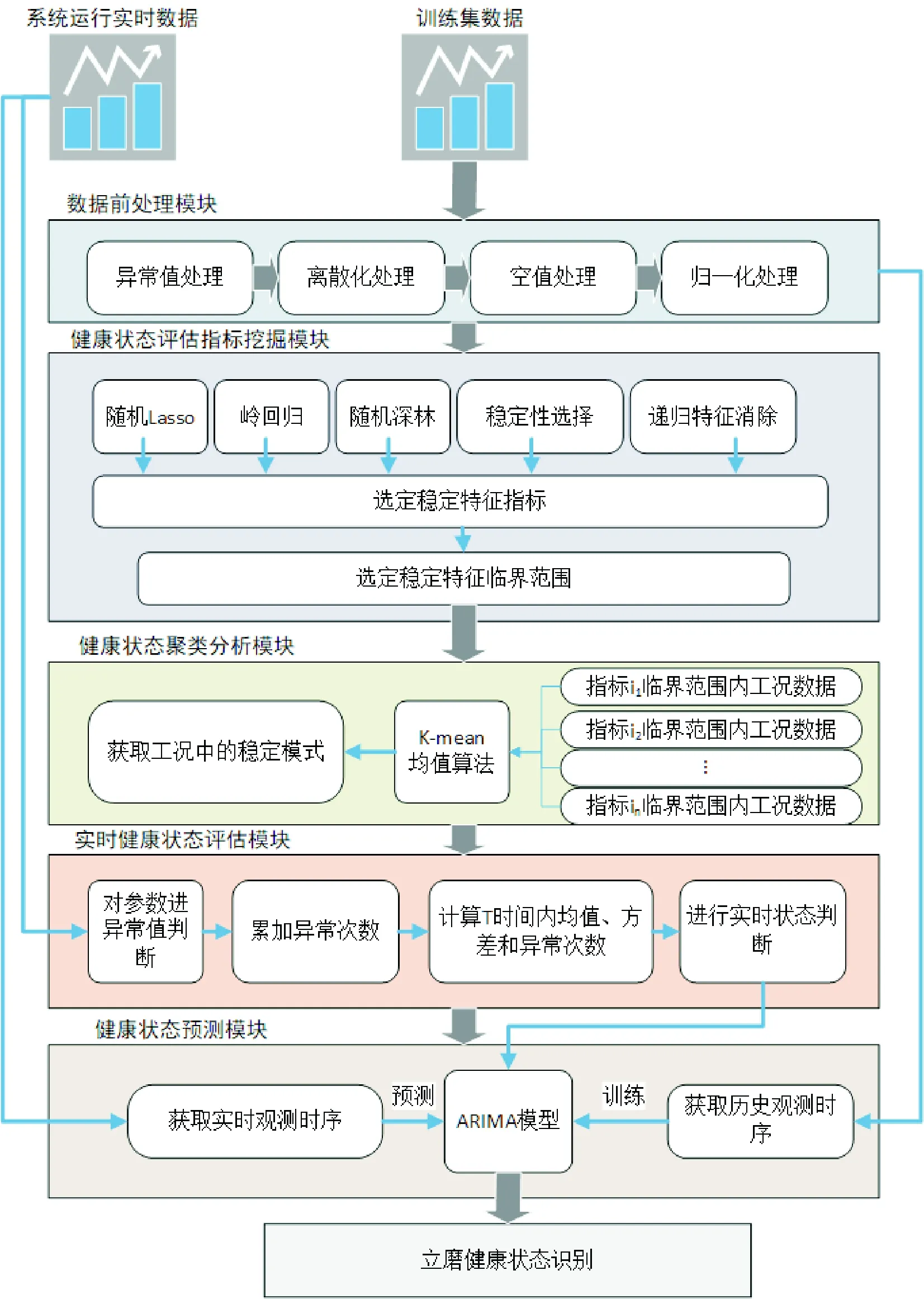
图4 系统总体结构图Fig.4 System general structure

上述5个模块分别以历史采样数据集和实时运行数据集作为输入，通过数据处理加工及挖掘分析共同实现矿渣粉磨系统的健康状态识别。

3 应用实例及分析

本系统已在河南某微粉厂投入运行，系统运行界面如图5所示。现场应用证明，该系统为立磨健康状态识别提供了更经济有效的决策，系统运行稳定。具体应用过程如下。

图5 系统运行界面图Fig.5 System operation interface diagram

3.1 数据获取及预处理

系统采用OPC协议实现数据通讯，通过向立磨中控系统服务器发送连接请求实时采集数据。系统可以设定采集的参数种类和采样间隔。

运行现场系统实际可采集各类数据信号参数65个。经过属性筛选、数据异常值处理及空值处理后得到30个立磨系统主要工艺和性能参数的属性子集。综合考虑立磨系统的工艺状态、生产人员人为设置以及实际运行中参数的可控性等情况，对数据进一步简化降维处理，最终剩余12个主要特征参数，包括喂料量、微粉比表、料层厚度、磨机出口温度、磨机进口温度、磨机进口压力、选粉机转速、磨机压差、主排风扇转速、冷风阀开度、热风阀开度和循环风阀开度。部分特征和特征值如表1所示。

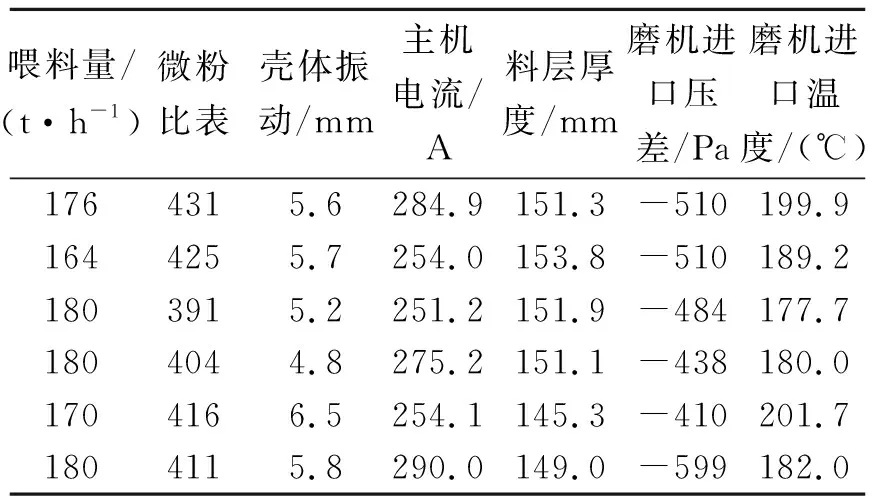
表1 特征筛选后的部分数据

可以看出，参数的量纲不一致，取值范围相差很大。为了消除取值范围和量纲不同对分析结果的影响，需要对数据进行规范化处理。为避免数据中存在极大值或极小值对后续分析产生影响，标准化方法采用零-均值方法，这种标准化方法和使用极大极小值标准化相比更加稳定。标准化之后的部分数据如表2所示。

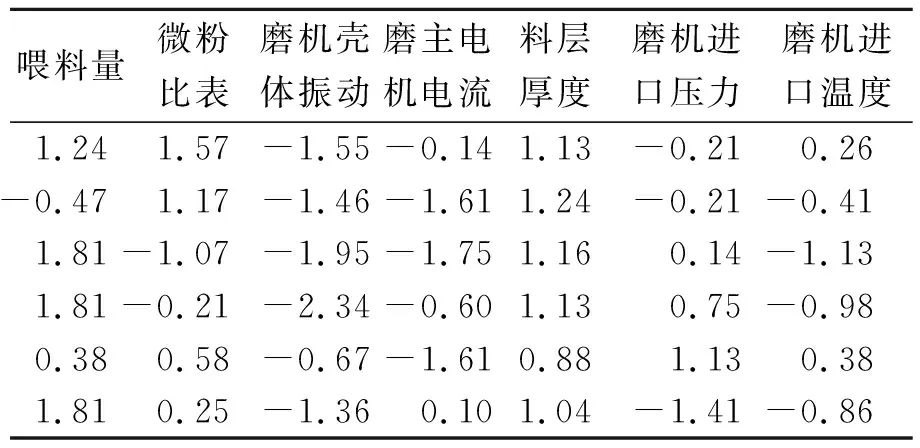
表2 标准化之后的部分数据(无量纲单位)

3.2 健康特征指标确定

在应用实例现场以2s为采样周期，持续15个工作日采集立磨系统运行状态下的12个主要参数。随机抽取其中3个工作日时段的运行数据作为样本，采用健康状态评估指标挖掘模块计算获取各参数属性指标评分。综合评分记录如表3所示。最终确定除壳体振动幅度外，磨机出口温度、料层厚度以及磨机压差共同作为立磨系统的健康状态特征。

表3K=3时待选特征的得分情况(无量纲单位)

Tab.3ThescoreresultoftheparameterofK=3

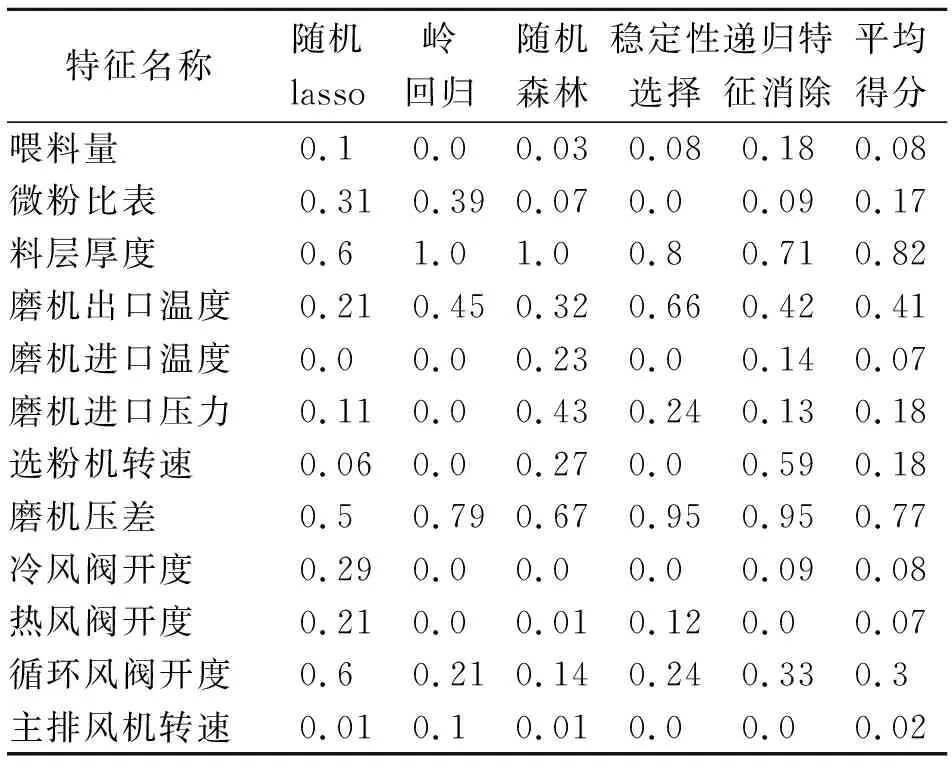
特征名称随机lasso岭回归随机森林稳定性选择递归特征消除平均得分喂料量0.10.00.030.080.180.08微粉比表0.310.390.070.00.090.17料层厚度0.61.01.00.80.710.82磨机出口温度0.210.450.320.660.420.41磨机进口温度0.00.00.230.00.140.07磨机进口压力0.110.00.430.240.130.18选粉机转速0.060.00.270.00.590.18磨机压差0.50.790.670.950.950.77冷风阀开度0.290.00.00.00.090.08热风阀开度0.210.00.010.120.00.07循环风阀开度0.60.210.140.240.330.3主排风机转速0.010.10.010.00.00.02

3.3 健康运行状态的工况聚类

利用健康状态聚类分析模块进行运行工况的聚类计算。健康状态聚类分析模块中K-means核心参数K需要根据工程现场数据结果进行迭代分析。笔者依次将K=2, 3,4分别代入样本数据开展计算。当K=2时形成两类数据，各参数范围的重叠性较大，不能很好地区分类别；当K=4时形成4类

数据，其中第1类和第3类的各参数聚类中心均比较接近，参数取值范围交叉较多；当K=3时，只是在壳体振动数值上有一定重合，但其他3个参数的距离间隔比较合理。图6为K=3时分群的参数分布概率密度图。表4为其聚类中心及每个簇中的数据点个数。

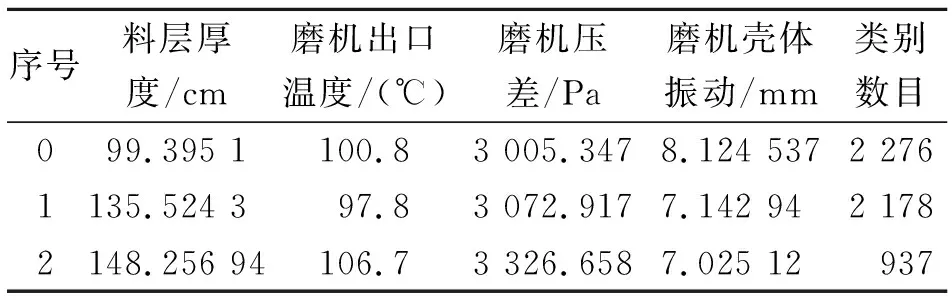
表4 分群聚类中心表(K=3)

结合立磨系统运行现场的生产人员建议，笔者确定取K=3作为最终聚类结果，并定义此时类别2为非健康状态，类别0和1为健康状态。类别0特点：壳体振动幅度集中在7～9mm，此时出口温度在100～108℃，料层厚度范围在125～135mm，磨机压差在2 800～3 200 Pa。类别1特点：壳体振动幅度为6～8mm，此时磨机出口温度为9～103℃，料层厚度在125～144mm，磨机压差在2 800～3 200 Pa。类别2特点：壳体振动幅度在6～9mm, 此时磨机出口温度在102～110℃，料层厚度在140～150mm，磨机压差在3 200～3 500 Pa。根据工况分类情况，依次从样本数据中抽取工况数据集合比对，建立系统健康工况模式库。

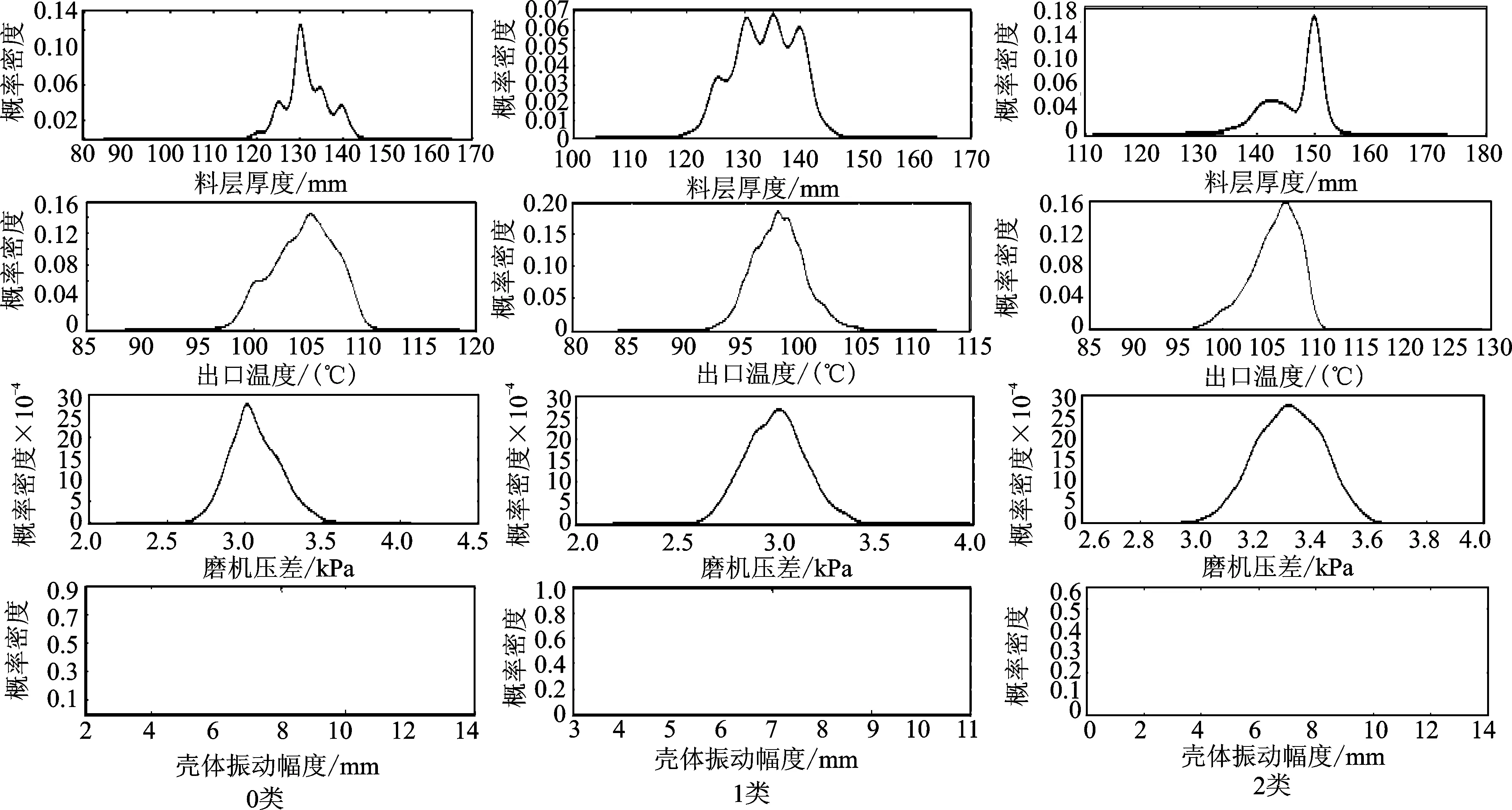
图6 时分群的参数分布概率密度图(K=3)Fig.6 The distribution probability density diagram of the parameter distribution (K=3)

3.4 健康状态识别与预测

针对壳体振动幅度、磨机出口温度、料层厚度及磨机压差这4个健康特征指标，利用实时健康状态评估模块分别计算每个参数实时运行数据在采集窗口时间内的均值、方差和异常值出现次数，把得到的结果作为稳定工况判断的特征变量与健康工况模式库中的状态进行比对。在具体操作中Δt=2s,n=15。生产人员可根据系统提供的运行状态信号判断系统当前运行状态是否健康。

以壳体振动幅度为例，说明采用时间序列进行稳定状态判断的过程。对一段时间内采集到的振动值进行平稳性检测，其原始序列图走势如图7所示。可以看出, 该序列有上升趋势，属于非平稳序列。对序列求取自相关系数，自相关图如图8所示。相关系数的绝对值长期大于零，说明该序列具有长期的相关性。对这个序列进行一阶差分后得到自相关图如图9所示。偏自相关图如图10所示。可以看出, 一阶差分后的序列在均值附近波动且波动范围不大，为平稳序列。

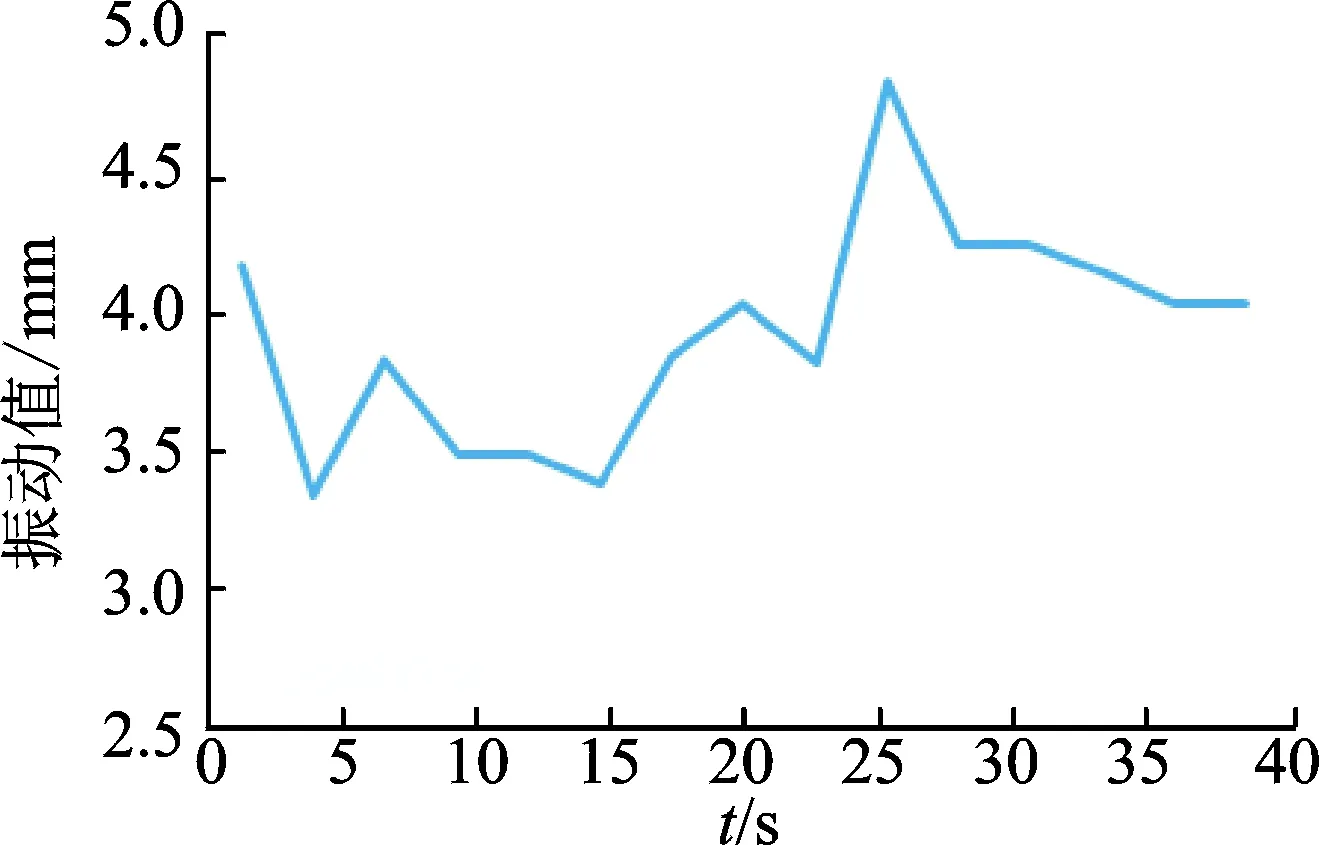
图7 振动一段时间内的原始序列图Fig.7 The vibration original sequence data diagram

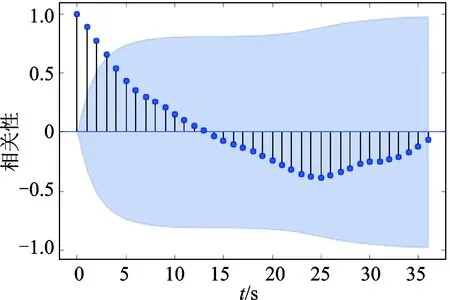
图8 振动一段时间内的原始序列自相关图Fig.8 The vibration original sequence autocorrelation diagram for a period of time

对一阶差分后的序列进行白噪声检测，得到的P值小于0.05，所以一阶差分后的序列属于平稳非白噪声序列，可以用ARIMA进行拟合。接下来对ARIMA进行定阶，也就是求模型中的参数。根据p，q的所有组合得到的贝叶斯信息准则(Bayesian information criterion，简称BIC)的信息量大小来确定，选择令BIC信息量达到最小的p，q组合。模型定阶后利用ARIMA进行预测。

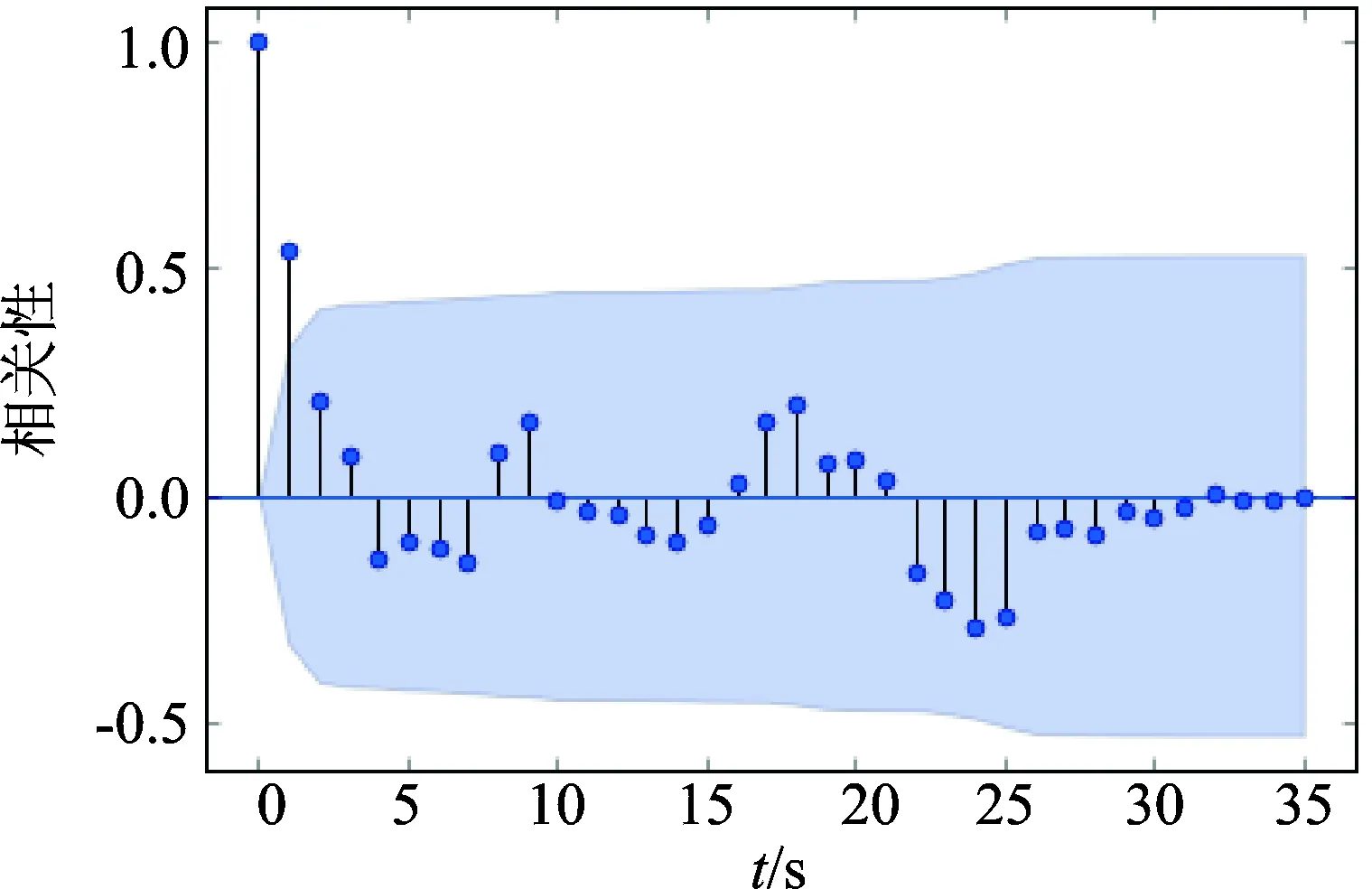
图9 振动一段时间内的原始序列一阶差分后的自相关图Fig.9 The autocorrelation diagram after first order difference of vibration original sequence in a period time

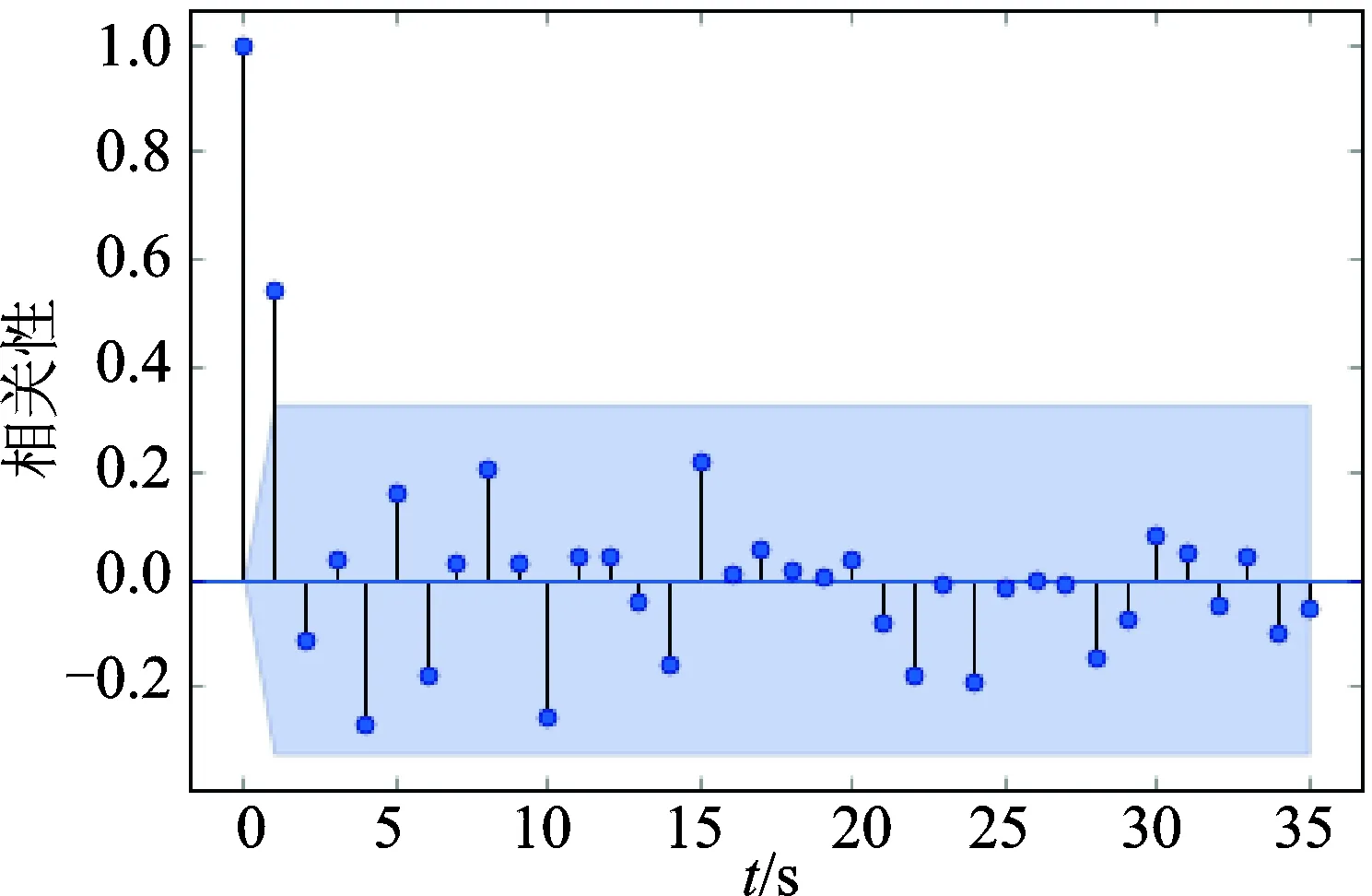
图10 振动一段时间内的原始序列一阶差分后的偏自相关图Fig.10 The partial autocorrelation diagram of first order difference of vibration original sequence in a period of time

预测模型可以给出连续5min的预测值、标准误差和置信区间，预测值和实际值的关系如图11所示。可以看出, 预测误差较低，预测值基本能够反映数值的变化趋势，模型的预测效果良好。

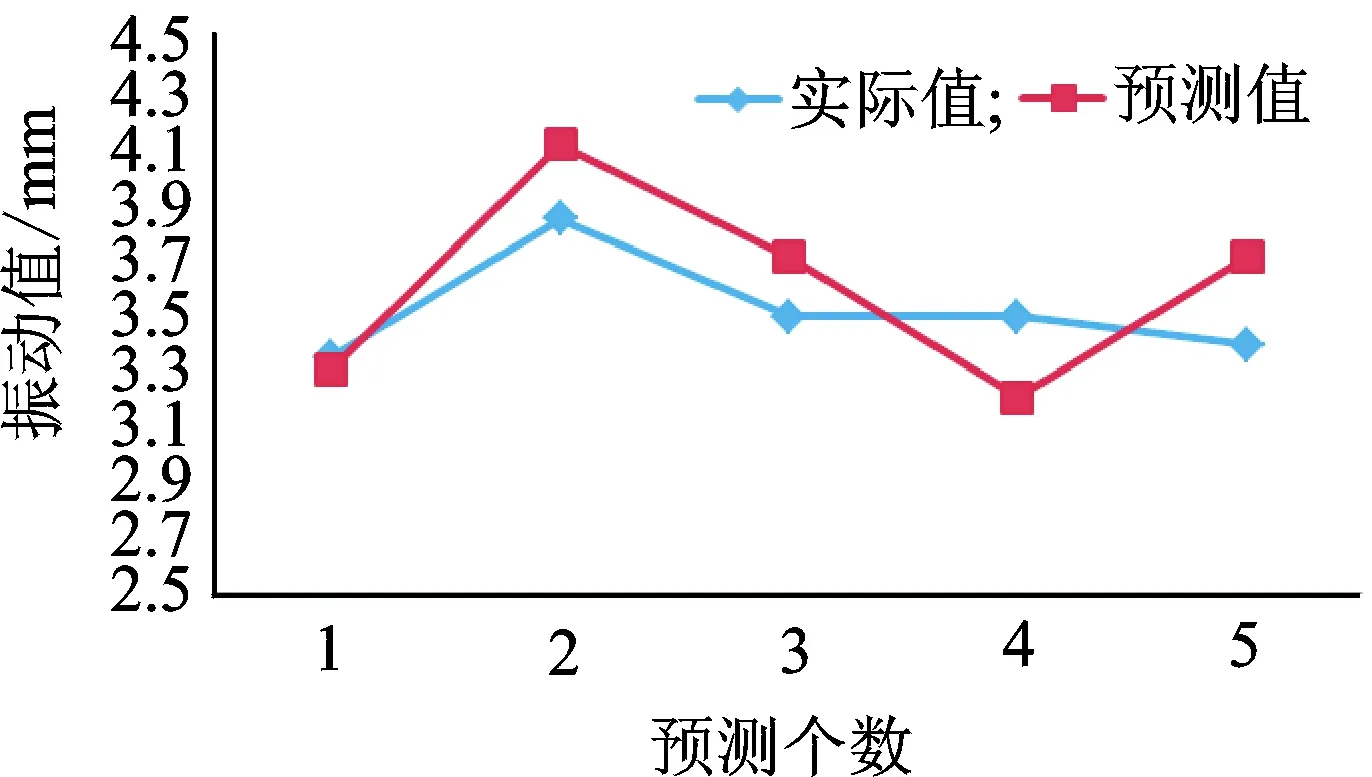
图11 模型的预测值和实际值比较Fig.11 Predicted value is compared to the actual value

4 结束语

提出一种基于数据挖掘的矿渣粉磨运行健康状态识别模型。首先，利用一种综合的特征筛选方法对工况数据进行挖掘分析，得到影响立磨稳定运行的关键参数，将其作为健康状态评估的指标；然后，对工况状态进行聚类挖掘分析，获得历史工况中的状态分布情况，定义历史工况中的健康运行状态类别；最后，利用ARIMA对建立系统健康状态特征训练模型，对系统运行参数的变化趋势进行预测，实现健康状态识别。该系统已在河南省某矿渣微粉厂投入运行。实践表明，该系统运行稳定、灵活高效，能满足工程实际应用。