基于PPTSVD的桥梁移动荷载识别

陈 震， 魏文杰， 余 岭， 邵文达

(1. 华北水利水电大学土木与交通学院 郑州，450045) (2. 暨南大学重大工程灾害与控制教育部重点实验室 广州，510632)

引 言

桥梁是铁路、公路等跨越江河、峡谷的重要连接，也是道路交通的咽喉。桥梁的安全性和可靠性对社会经济的发展有深远影响。随着我国经济建设的迅猛发展，车流量急剧增大，桥梁结构在使用过程中深受移动荷载侵扰，且高速、超载的车辆移动荷载对其破坏严重，严重影响桥梁的安全性能。在桥梁工程中，移动荷载识别与健康监测、桥梁振动及受损桥梁的工作性能研究[1]等密切相关。

移动荷载识别问题的研究最早始于19世纪初期，此后许多学者开始关注并提出了多种识别方法。Luo等[2]提出了采用TDM识别桥梁移动荷载，并对结构动力学逆问题采用SVD求解。卜建清等[3]比较了板梁桥振动响应求解方法。王蕾等[4]采用拟合函数逼近法识别移动荷载。Xu等[5]应用虚功原理提出了拟合动态荷载的移动最小二乘法。Qiao等[6]基于三次B样条扩展函数提出了精确度高且能克服不适定问题的移动荷载识别方法。Chen等[7]采用计算机视觉技术模拟桥面荷载的时空分布。Talukdar等[8]采用粒子滤波法识别车辆荷载参数。

虽然TDM采用SVD分解进行降噪处理，是一种较为有效的移动荷载识别方法，但仍存在识别精度较低、抗噪性差和采用弯矩响应识别结果不可接受等缺点。陈震等[9]在TDM的基础上提出截断广义奇异值分解法，对移动荷载识别精度有一定程度的提高。笔者提出的PPTSVD是一种以TSVD为基础的正则化方法。数值仿真结果表明，与TDM和TSVD相比，基于PPTSVD识别桥梁移动荷载的识别精度更高、识别结果受响应类型及响应组合影响更小，具有良好的鲁棒性，更适用于桥梁移动荷载的现场识别。

1 基本理论

1.1 移动荷载识别理论

以简化欧拉梁模型为例，假定桥梁全长为L，单位长度质量为ρ，取桥梁阻尼为黏性阻尼C，抗弯刚度为EI。如图1所示，车辆模型简化为移动荷载，车辆重量为P，车速为c，车辆从梁左端向右端匀速行驶，车桥模型模态坐标方程可表示为

(n=1,2,,∞)

(1)

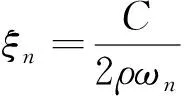
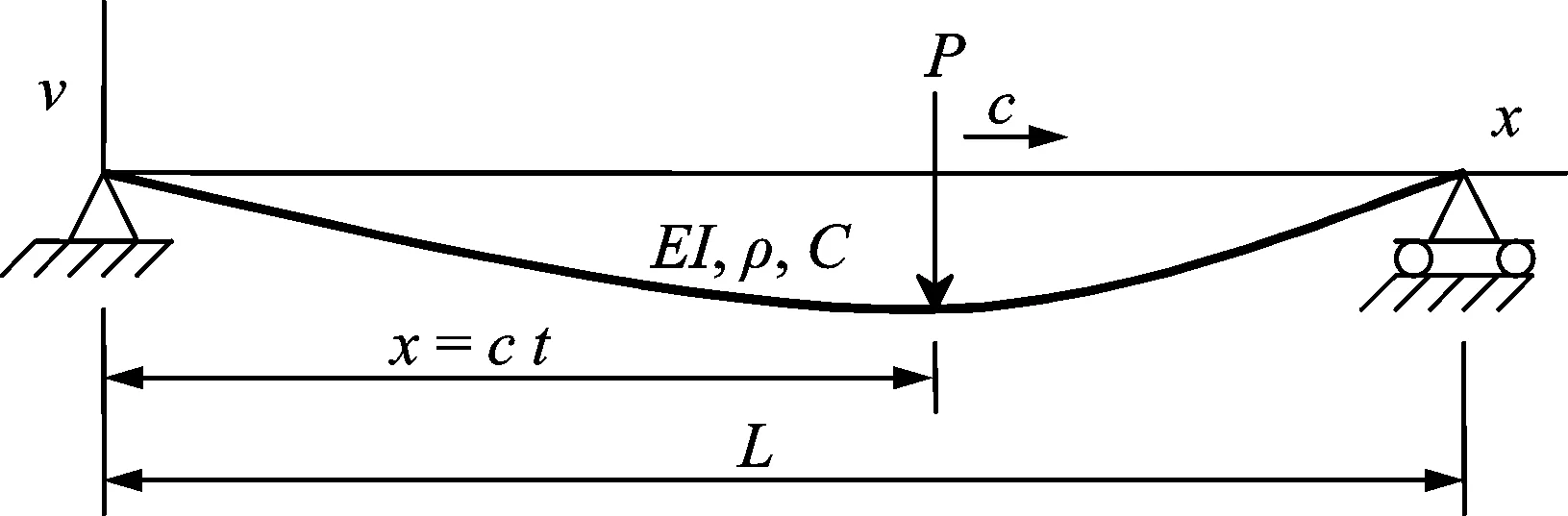
图1 简化车桥模型Fig.1 Simplified model of vehicle and bridge

1.2 时域法

基于TDM基本理论，通过对式(1)在时域卷积积分，得到车辆荷载作用下梁上x处t时刻的变形为

(2)

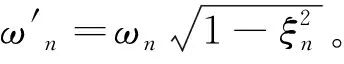
梁上x处t时刻的弯矩为

(3)

将ν求二阶导数，梁上x处t时刻的加速度为

(4)

其中

(5)

当测得车辆荷载作用下桥梁的弯矩响应和加速度响应后，TDM移动荷载识别理论最终可转化为系统方程求解问题。

Ax=b

(6)

其中：A为车桥模型系统矩阵；b为测得的桥梁响应；x为待识别的桥梁移动荷载。

1.3 分段多项式截断奇异值分解

PPTSVD算法是以TSVD为基础的正则化方法，文献[10]指出，PPTSVD正则化方法在信号处理方面较传统的基于SVD的正则化方法能够取得更好的效果。

1.3.1 奇异值分解

m行n列的车桥系统矩阵A可由SVD表示为

(7)

其中：U和V均为方阵且满足UTU=VTV=In；Σ为对角元素是σi的对角矩阵，即Σ=diagσ1,σ2,,σn；σ1≥σ2≥σ3≥≥σn≥0为A的奇异值。

在信号识别过程中，可通过调整Σ滤除无关信号和部分噪声。

1.3.2 截断奇异值分解

TSVD方法通过截断噪声引起的小奇异值，保留包含真实信号信息的大奇异值来降低噪声对识别结果的影响。用截断后的矩阵Ak代替原有系数矩阵A

(8)

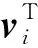
TSVD的解xk为

(9)

TSVD在截断由噪声引起的小奇异值的同时会丢弃部分有效信号。如能在滤除噪声信号的同时保留有效信号，并将有效信号叠加到原TSVD解中，求解结果将更理想。PPTSVD方法正是基于这一思路，在TSVD截断信号中提取有效信号，进而提高移动荷载识别精度。

1.3.3 分段多项式截断奇异值分解

(10)

其中：LP为离散近似微分算子；p通常取值为1和2，其对应的L1和L2可表示为

(11)

(12)

PPTSVD方法可由TSVD改进得到，PPTSVD的解由TSVD的解xk和一个由截断信号中提取的修正参数-Vn-kωk组成，其中：Vn-k=(vk+1,vk+2，,vn)为截断信号构成的矩阵，其为矩阵V的子矩阵；ωk可由求解如下最小线性二乘问题得到

(13)

(14)

移动荷载识别数值模拟结果表明，采用近似微分算子L1的识别精度较采用近似微分算子L2有明显提高，故有关PPTSVD移动荷载识别数值模拟均采用近似微分算子L1。图2为PPTSVD方法流程图。

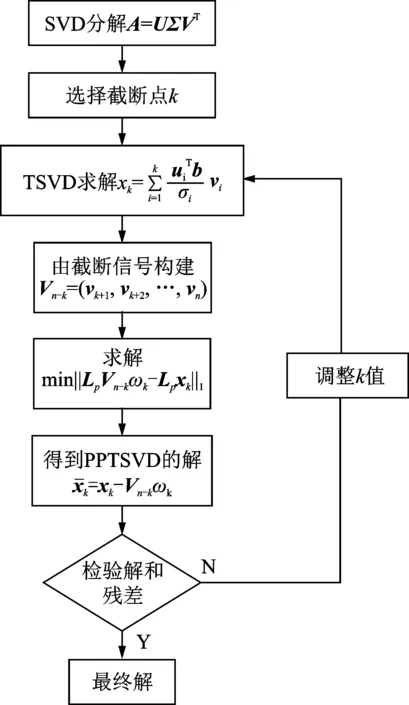
图2 PPTSVD流程图Fig.2 Flow diagram of PPTSVD

2 仿真算例

车辆模型参数如下：车辆前后轴间距ls=8 m，行驶速度c=40 m/s。桥梁模型参数如下：梁长L=40 m；单位长密度ρ=12 000 kg/m；抗弯刚度EI=1.28×1011N·m2；前3阶固有频率f1=3.2 Hz，f2=12.8 Hz，f3=28.8 Hz。测量响应数据时采样频率取200 Hz，分析频段取0～40 Hz。桥面行驶车辆的前轴和后轴荷载分别为

f1t=20[1+0.1sin1/4cπt+0.05×

sincπt]kN

f2t=20[1-0.1sin1/4cπt+0.05×

sin5/4cπt]kN

为模拟现场测量响应信号时噪声干扰，取包含噪声的桥梁响应为

Mmeasured=Mcalculated1+EPNoise

(15)

其中：EP(0≤EP≤1)为噪声水平，分别取其为1%，5%和10%；Noise为随机噪声且满足标准正态分布。

由测量响应识别桥梁移动荷载的相对误差为

(16)

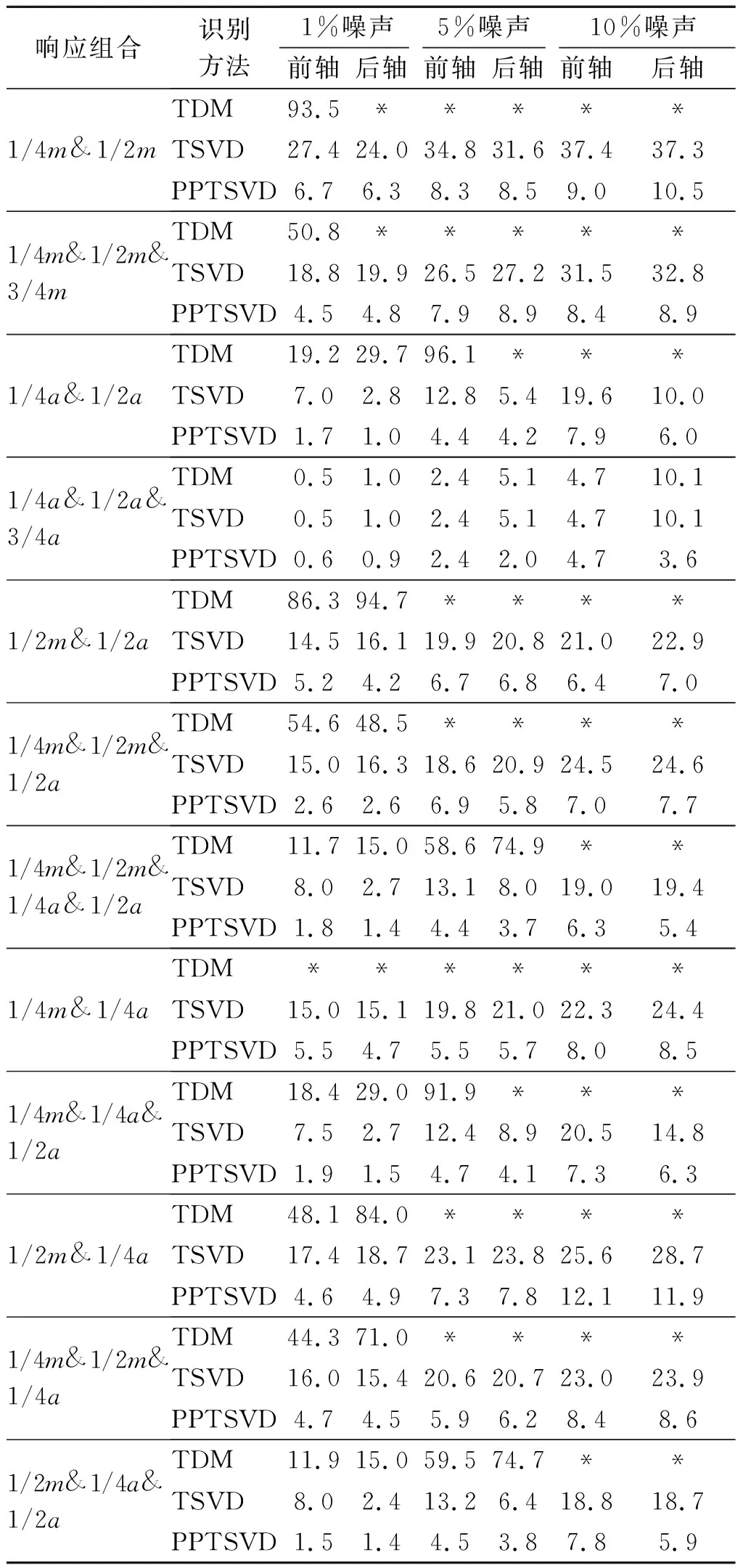
表1为12种组合工况下TDM，TSVD和PPTSVD在3种噪声水平下的识别误差。表2为对应表1中TSVD与PPTSVD识别结果所选取的最优截断点k值。表中1/4，1/2和3/4分别表示测点所在桥梁位置为1/4桥跨、1/2桥跨和3/4桥跨；m为测量弯矩响应；a为测量加速度响应；*表示识别误差超出最大上限值100%。由车桥系统矩阵A列数为396可知，截断点k的取值范围为1≤k≤n。当截断点取396时，此时没有对奇异值进行截断，TSVD方法退化为SVD方法，其识别结果与SVD一致。由表2可知，当响应组合为1/4a&1/2a&3/4a时，截断点取最大值396，此时表1中TDM和TSVD两种方法的识别误差相同。

由表1可知，3种识别方法的识别误差均随着测量噪声增大而增大，当噪声水平达到10%时，TDM对应的12种工况中有11种工况识别误差均超过100%，识别结果不能接受。TSVD在12种识别工况中识别结果均能接受，其中有10种工况识别误差低于30%，抗噪性能较TDM提高明显，这表明通过截断噪声信号提高移动荷载识别精度和抗噪性能是可行的。PPTSVD对应12种工况识别误差均低于15%，且其中10种工况识别误差低于10%，其抗噪性能较TSVD有较大提高，这说明通过提取截断噪声中的有效信号并将其作为修正解叠加到TSVD的解中是有效的。通过对TDM默认的SVD方法进行噪声截断并用分段多项式逼近真实解对提高桥梁移动荷载识别精度和抗噪性能具有良好的适用性。

表1TDM，TSVD与PPTSVD识别结果RPE值比较

Tab.1ComparisononRPEvaluesidentifiedbyTDM,TSVDandPPTSVD

响应组合识别方法1%噪声5%噪声10%噪声前轴后轴前轴后轴前轴后轴1/4m&1/2mTDM93.5*****TSVD27.424.034.831.637.437.3PPTSVD6.76.38.38.59.010.51/4m&1/2m&3/4mTDM50.8*****TSVD18.819.926.527.231.532.8PPTSVD4.54.87.98.98.48.91/4a&1/2aTDM19.229.796.1***TSVD7.02.812.85.419.610.0PPTSVD1.71.04.44.27.96.01/4a&1/2a&3/4aTDM0.51.02.45.14.710.1TSVD0.51.02.45.14.710.1PPTSVD0.60.92.42.04.73.61/2m&1/2aTDM86.394.7****TSVD14.516.119.920.821.022.9PPTSVD5.24.26.76.86.47.01/4m&1/2m&1/2aTDM54.648.5****TSVD15.016.318.620.924.524.6PPTSVD2.62.66.95.87.07.71/4m&1/2m&1/4a&1/2aTDM11.715.058.674.9**TSVD8.02.713.18.019.019.4PPTSVD1.81.44.43.76.35.41/4m&1/4aTDM******TSVD15.015.119.821.022.324.4PPTSVD5.54.75.55.78.08.51/4m&1/4a&1/2aTDM18.429.091.9***TSVD7.52.712.48.920.514.8PPTSVD1.91.54.74.17.36.31/2m&1/4aTDM48.184.0****TSVD17.418.723.123.825.628.7PPTSVD4.64.97.37.812.111.91/4m&1/2m&1/4aTDM44.371.0****TSVD16.015.420.620.723.023.9PPTSVD4.74.55.96.28.48.61/2m&1/4a&1/2aTDM11.915.059.574.7**TSVD8.02.413.26.418.818.7PPTSVD1.51.44.53.87.85.9

图3为1%噪声水平下TDM，TSVD与PPTSVD采用弯矩响应的识别结果。图4为5%噪声水平下3种识别方法采用加速度响应的识别结果。图5为10%噪声水平下3种识别方法采用弯矩和加速度组合响应的识别结果。

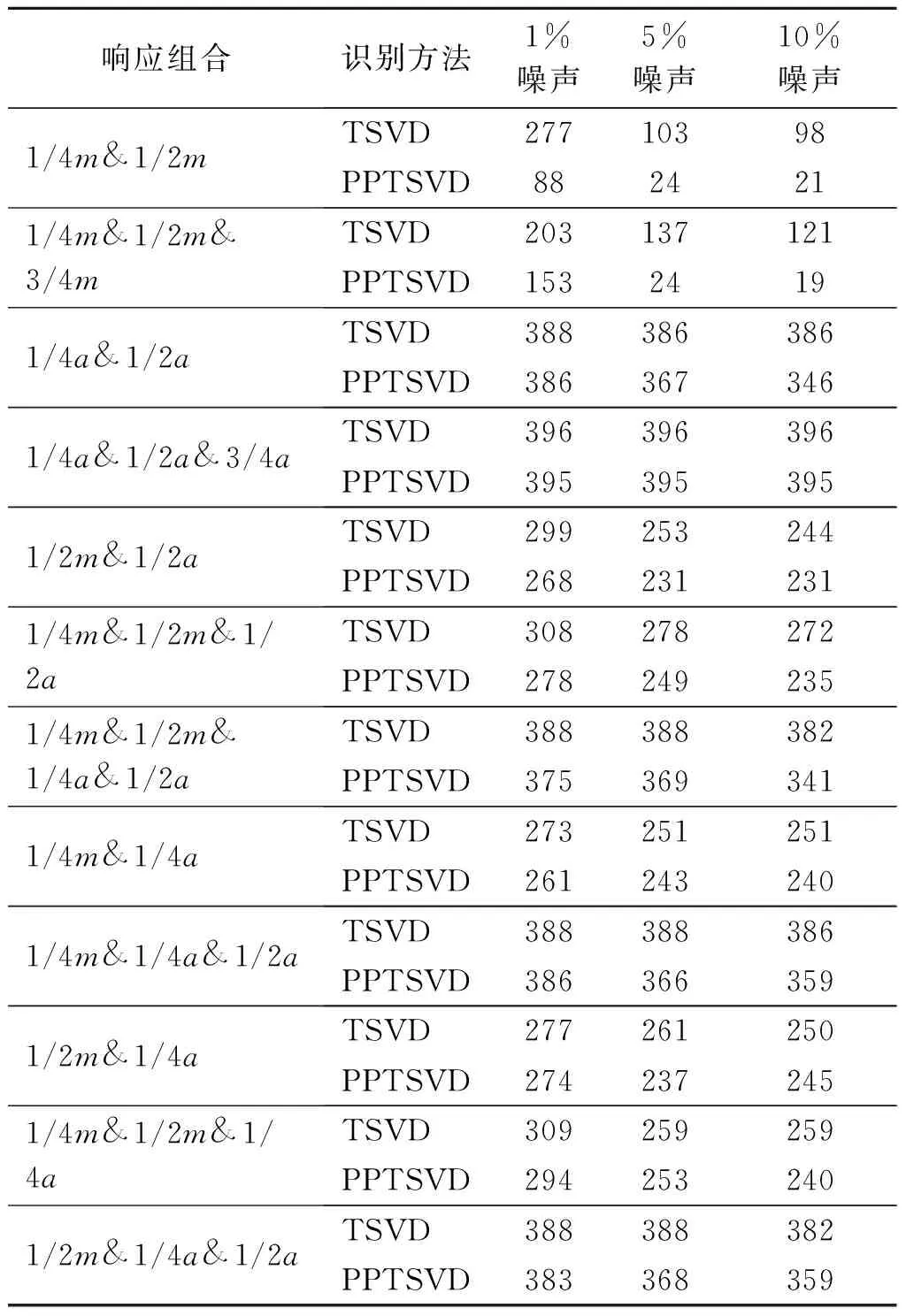
由表2可知，最优截断点随工况不同有所变化，总体来说，当响应组合全部采用加速度信号时，最优截断点非常接近系统矩阵列数，即只需截断极少数噪声信号即可有效识别移动荷载，这说明噪声对高频的加速度信号干扰较小，采用加速度响应识别时3种方法识别精度均较高，识别结果如图4所示。

表2TSVD与PPTSVD最优截断点k比较

Tab.2ComparisononthebesttruncatedpointkofTSVDandPPTSVD

响应组合识别方法1%噪声5%噪声10%噪声1/4m&1/2mTSVD27710398PPTSVD8824211/4m&1/2m&3/4mTSVD203137121PPTSVD15324191/4a&1/2aTSVD388386386PPTSVD3863673461/4a&1/2a&3/4aTSVD396396396PPTSVD3953953951/2m&1/2aTSVD299253244PPTSVD2682312311/4m&1/2m&1/2aTSVD308278272PPTSVD2782492351/4m&1/2m&1/4a&1/2aTSVD388388382PPTSVD3753693411/4m&1/4aTSVD273251251PPTSVD2612432401/4m&1/4a&1/2aTSVD388388386PPTSVD3863663591/2m&1/4aTSVD277261250PPTSVD2742372451/4m&1/2m&1/4aTSVD309259259PPTSVD2942532401/2m&1/4a&1/2aTSVD388388382PPTSVD383368359

图3 TDM, TSVD与PPTSVD由弯矩响应识别移动荷载结果比较1/4m&1/2m&3/4m(EP=1%)Fig.3 Identified biaxial time-varying forces with TDM, TSVD and PPTSVD from bending responses 1/4m&1/2m&3/4m, (EP=1%)

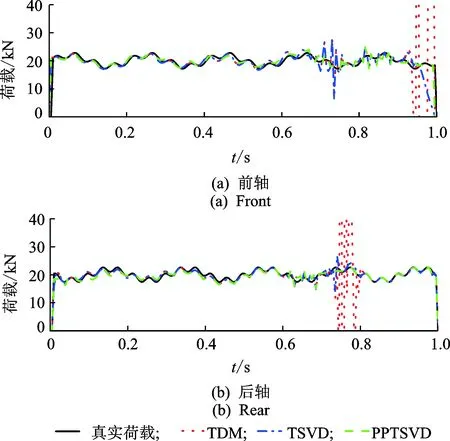
图4 TDM，TSVD与PPTSVD由加速度响应识别移动荷载结果比较1/4a&1/2a (EP=5%)Fig.4 Identified biaxial time-varying forces with TDM, TSVD and PPTSVD from acceleration responses 1/4a&1/2a (EP=5%)

由表2可知，当响应组合中包含弯矩响应时，最优截断点取值随弯矩响应比例增加而降低，当响应组合全部为弯矩响应时最优截断点最小。这说明噪声对低频的弯矩响应影响较大，需要截断较多的噪声干扰信号。TDM默认的SVD方法不能截断噪声干扰信号，因此在识别包含弯矩响应的组合工况时精度最低，尤其当仅由弯矩响应识别移动荷载时识别结果不能接受，如图3所示。

TSVD在识别包含弯矩响应的组合工况时识别精度较TDM有明显提高，但由于截断大量的噪声干扰信号也必然会丢弃部分隐藏在噪声信号中的真实响应，因此识别结果不太理想。PPTSVD通过提取截断噪声信号中的真实响应并将其作为修正值叠加到TSVD解中，弥补了TSVD存在的缺陷，其理论最完备且识别精度和抗噪性能在3种方法中均为最优，识别结果如图3～5所示。

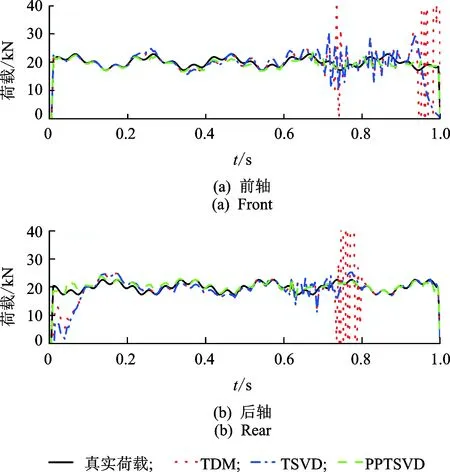
图5 TDM, TSVD与PPTSVD由组合响应识别移动荷载结果比较1/4m&1/2m&1/4a&1/2a (EP=10%)Fig.5 Identified biaxial time-varying forces with TDM, TSVD and PPTSVD from combination responses 1/4m&1/2m&1/4a&1/2a (EP=10%)

3 结 论

1) PPTSVD方法通过提取截断噪声信号中的真实响应并将其作为修正值叠加到TSVD解中，很好地弥补了TSVD存在的缺陷，具有良好的理论完备性。

2) 噪声对高频的加速度信号干扰较小，当响应组合全部采用加速度信号时，TSVD和PPTSVD最优截断点均与系统矩阵列数非常接近，即只需截断极少数噪声信号即可有效识别移动荷载，此时3种方法识别精度均较高。

3) 噪声对低频的弯矩响应影响较大，需要截断较多的噪声干扰信号。TDM默认的SVD方法不能截断噪声干扰信号，因此在识别包含弯矩响应的组合工况时精度较低。TSVD较TDM有明显的提高，但由于丢弃了较多隐藏在噪声信号中的真实响应，识别结果仍不理想。PPTSVD通过提取截断噪声信号中的真实响应并将其作为修正值叠加到TSVD解中，较完美地解决了这一问题。

4) 多工况研究表明，PPTSVD在各种响应组合下均具有较高的识别精度，其良好的响应组合适应性有利于测点较少、响应类型单一环境下移动荷载识别。

5) 提出的PPTSVD方法在移动荷载识别领域具有识别精度高、鲁棒性好以及响应组合适应性强等优点。在实际移动荷载识别过程中，桥面平整度、车速和轴重等参数对识别精度也有一定的影响，对该方法的现场适用性有待于进一步研究和校核。