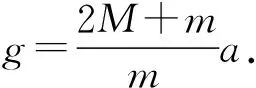源于经典 守正创新——评析2018年江苏高考第11题

李俊成

(南京市第九中学,江苏 南京 210018)

1 考题及答案

图1

原题.某同学利用如图1所示的实验装置来测量重力加速度g.细绳跨过固定在铁架台上的轻质滑轮,两端各悬挂一只质量为M的重锤.实验操作如下:

① 用米尺量出重锤1底端距地面的高度H;

② 在重锤1上加上质量为m的小钩码;

③ 左手将重锤2压在地面上,保持系统静止.释放重锤2,同时右手开启秒表,在重锤1落地时停止计时,记录下落时间;

④ 重复测量3次下落时间,取其平均值作为测量值t.

请回答下列问题：

(1) 步骤④可以减小对下落时间t测量的________误差(选填“偶然”或“系统”).

(2) 实验要求小钩码的质量m要比重锤的质量M小很多,主要是为了________.

(A) 使H测得更准确.

(B) 使重锤1下落的时间长一些.

(C) 使系统的总质量近似等于2M.

(D) 使细绳的拉力与小钩码的重力近似相等.

(3) 滑轮的摩擦阻力会引起实验误差.现提供一些橡皮泥用于减小该误差,可以怎么做?

(4) 使用橡皮泥改进实验后,重新进行实验测量,并测出所用橡皮泥的质量为m0.用实验中的测量量和已知量表示g,得g=________.

2 源于经典

考题是2018江苏高考物理第11题,该题源于经典物理模型——阿特伍德机(Atwood machine,又译作阿特午德机或阿特午机),阿特伍德机是由英国牧师、数学家兼物理学家乔治·阿特伍德(George Atwood,1746—1807)提出的一种用于测量加速度及验证运动定律的机械.其基本结构就是如图1所示,在跨过定滑轮的轻绳两端悬挂两个质量相等的物块,当在一物块上附加另一小物块时,该物块即由静止开始加速滑落,经一段距离后附加物块自动脱离,系统匀速运动,测得此运动速度即可求的重力加速度.一个理想的阿特伍德机包含质量为m1和m2的两个物体,及由无重量、无弹性的绳子连结并包含理想且无重量的滑轮. 当m1、m2相等时,机械处于力平衡的状态.当m1、m2相不等时,两物体有相同的等加速度.理想化的阿特伍德机模型在中学物理教学中经常出现,比如这样的模考题.

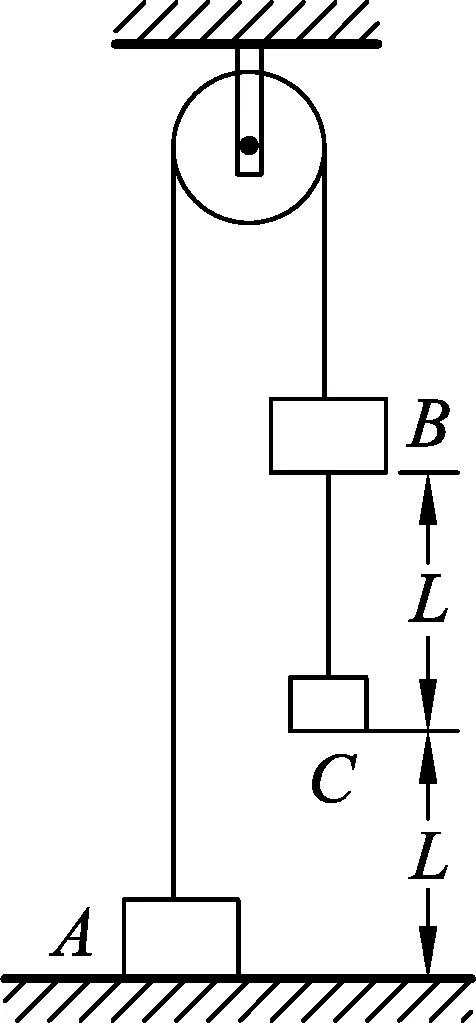
图2

如图2所示,物块A、B、C的质量分别为2m、2m、m,并均可视为质点,3个物块用轻绳通过轻质滑轮连接,在外力作用下现处于静止状态,此时物块A置于地面,物块B与C、C到地面的距离均是L,现将3个物块由静止释放.若C与地面、B与C相碰后速度立即减为0,A距离滑轮足够远且不计一切阻力,重力加速度为g.求:

(1) 刚释放时A的加速度大小及轻绳对A的拉力大小;(F=2.4mg)

(2) 物块A由最初位置上升的最大高度;(h=0.2L)

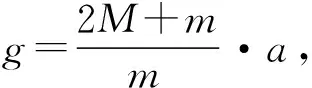
3 守正创新

图3

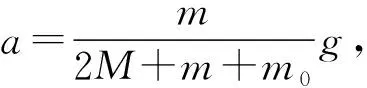
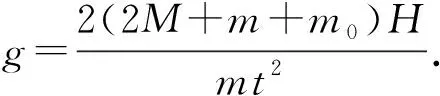
4 启发备考

纵观前面的分析,可以看出考题以牛顿第二定律为知识载体,考查了应用物理规律处理实际问题的科学思维和科学探究能力.牛顿运动定律是动力学的核心内容,同时也是高考的重要考点,然而自2003年课程改革以来江苏高考(即2008年江苏高考独立命题)开始,对牛顿运动定律的考查一直比较简单,局限于考查单个物体.当然这也是由于受往年江苏高考《考试说明》中“不要求定量求解加速度大小不同的连接体”的限制.自2013年江苏高考《考试说明》对这一要求做了修订,改为“加速度大小不同的连接体问题的计算仅限于两个物体的情况”以后,2013年的江苏高考第14题、2014年江苏高考第8题、2016年江苏高考第9题均以板块模型为载体考查了加速度大小不同、方向相同的连接体问题.今年高考以阿特伍德机模型为载体考查考查加速度大小相同、方向不同的连接体问题,可谓是江苏高考对牛顿运动定律考查的新动向,值得引起高考复习备迎考的关注.在复习过程中,可以在下列类似题的分析求解中提升解决这类问题的能力,提升考生的物理核心素养.

例1.在用如图3所示装置,探究加速度和力、质量间的关系实验中,水平面光滑,滑轮的质量和摩擦不计,试分析为使细绳的拉力与钩码的重力近似相等,钩码的质量m与小车的质量M必须满足的关系.

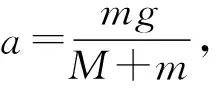
例2.(南京市2017届高三年级第3次模拟考试第14题)如图4所示,水平地面上有质量分别为1 kg和4 kg的物体A和B,两者与地面的动摩擦因数均为0.5,非弹性轻绳的一端固定且离B足够远,另一端跨过轻质滑轮与A相连,滑轮与B相连,初始时,轻绳水平,若物体A在水平向右的恒力F=31 N作用下运动了4 m,重力加速度g=10 m/s2,求

图4

(1) 物体B因摩擦而产生的热量;

(2) 物体A运动4 m时的速度大小;

(3) 物体A、B间轻绳拉力的大小;

解析: (1) 由于动滑轮的作用,物体A、B的位移满足位移xA=2xB,xA=4 m,则B的位移xB=2 m,B因摩擦而产生的热量Q=fB·xB=40 J.

(2) 设轻绳拉力为FT,A物体受的摩擦力为fA,加速度为aA.由牛顿第二定律得F-fA-FT=mAaA.设B物体物体受的摩擦力fB,加速度为aB,2FT-fB=mBaB.则由于动滑轮的作用,加速度间的关系满足aA=2aB,解得

代入数据得aA=8 m/s2.由运动学公式得v2=2aAsA,代入数据解得A运动4 m时的速度大小v=8 m/s.

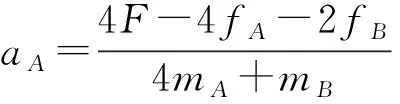
图5

(1) 刚释放C时,C的加速度大小;

(2)C从开始释放到速度最大的过程中,B上升的高度;

(3) 若A不离开地面,其质量应满足什么条件.

5 方法提升

从前面的分析,可以看出采取的方法都是隔离法.所谓隔离法,就是将所研究的对象(包括物体、状态和某些过程),从系统或全过程中隔离出来进行研究的方法.若连接体内各物体的加速度大小或方向不同时,一般应将各个物体隔离出来,分别对各个物体根据牛顿定律列式,并要注意找到各物体之间加速度的制约关系.这类问题之所以主要采用隔离法,就是由于加速度的方向不同.其实这类问题比较特殊,尤其是加速度大小相同时,也可以采取整体法.所谓整体法,就是将两个或两个以上物体组成的整个系统或整个过程作为研究对象进行分析研究的方法,整体法一般适用于系统中各部分物体的加速度大小、方向都相同的情况.最后,以考题为例体会整体法在这类问题求解中的应用.