小球在圆弧轨道上滚动与滑动的对比分析

赵清锋

(武汉市卓刀泉中学建和分校，湖北 武汉 430065)

简谐运动一直是物理竞赛中的热点考题.在第34届全国中学生物理竞赛预赛试题的第6、16两题,以及复赛理论试题的第一题都考察了简谐运动的情况,而圆弧轨道上的简谐运动又是考察的重点．同时圆弧轨道上的简谐运动以及相关动力学特性也是大学理论物理学习的重点.基于此本文借助圆弧轨道,针对均质小球无摩擦滑动和无滑滚动问题的振动周期进行分析.首先应用动力学特性求出两种情况小球运动的微分方程,并给出平衡位置微振动的周期;然后从机械能守恒角度对以上两种情况进行比较分析,发现无滑滚动周期可以直接借助无摩擦滑动得到;最后将相关结论应用于竞赛题中的圆柱滚动问题．

1 基本模型及两种情况微振动周期

图1

一个半径为r、质量为m的均质实心圆球被置于一个半径为R的固定圆筒中,圆筒的中心轴水平,横截面如图1所示.θ为某时刻小球质心到圆筒中心轴的垂线与竖直方向的夹角,两种情况下小球都受到重力mg和支持力FN.考虑两种情况下小球在其平衡位置的微振动周期.

(1) 小球无摩擦滑动.

考虑小球质心的运动,由牛顿第二定律可得

-mgsinθ=ma，

联立以上两式，化简即可得到微分方程

由小角近似sinθ≈θ,代入(1)式可得小球无摩擦滑动对应微振动周期

(2) 小球无滑滚动.

此时小球除了受到重力mg和支持力FN以外,还受到圆筒对其的静摩擦力f,考虑小球质心运动,由牛顿运动定理得

f-mgsinθ=ma.

(3)

由于小球与圆柱之间为无滑滚动,小球转过角度θ1(规定小球在最低点时θ1=0)与θ之间的关系为

Rθ=r(θ+θ1).

(4)

由(4)式可得a与θ的关系为

考虑小球绕过其球心且平行于圆筒的轴转动,由转动定理得

其中I为小球绕过其球心轴的转动惯量

由(3)～(7)式可得无滑滚动小球在圆弧轨道上运动的微分方程

由小角近似sinθ≈θ,代入(8)式可得小球无滑滚动对应微振动周期

2 能量角度对以上两种情况的对比分析

分析以上两种情况,无摩擦滑动和无滑滚动均没有机械能损失,但从计算的微振动周期结果看T2>T1,即无滑滚动时周期更长,分析原因在于无滑滚动中滚动动能取代了部分平动动能,而总的机械能守恒,从而使质心平动速度慢一些导致运动周期更长．

设两种情况下小球初始时与竖直方向的夹角都为θ0,当小球运动到θ位置时,对无摩擦滑动应用机械能守恒定律有

对无滑滚动应用机械能守恒有

小球绕过其质心的轴转动对应的转动惯量和角速度分别为

将(12)式代入(11)式,用平动动能取代转动动能,化简可得

比较(10)、(13)两式可得

上式即表示在任意相同的位置,两种情况所对应小球的速度之比为上述结果,且小球经历的路径相同,根据运动规律

∑si=∑viti，

(15)

可得两种情况下小球微振动周期之比为

这与(2)、(9)所对应的结果一致．

上文中(2)式这一结果在很多文献中有所研究,[1,2]教科书中也将其作为经典模型讲解．[3]一般情况下可以将(2)式对应结果直接使用,然后在借助能量分析计算其他模型与无摩擦滑动速度的比值,从而得到周期的比值关系,进而得到其他模型的周期．

3 能量守恒分析圆柱模型的周期

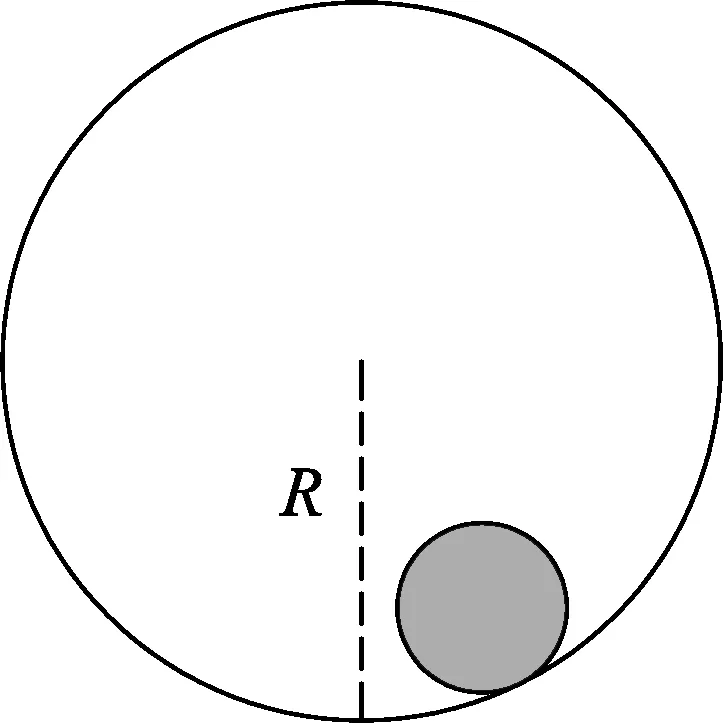
图2

例.(第34届全国中学生物理竞赛复赛理论考试第一题)一个半径为r、质量为m的均质实心小圆柱被置于一个半径为R、质量为M的薄圆筒中,圆筒和小圆柱的中心轴均水平,横截面如图2所示．重力加速度为g．圆筒固定,小圆柱在圆筒内底部附近做无滑滚动,求小圆柱质心在其平衡位置附近做微振动的频率．(原题有两问,本题只分析第1问).

解析:能量守恒方法.

设初始时小圆柱质心在其横截面上到圆筒中心轴的垂线与竖直方向夹角为θ0,当小球运动到θ位置时,对小圆柱应用机械能守恒定律有

小圆柱绕过其质心的轴转动对应的转动惯量和角速度分别为

将(18)式代入(17)式,用平动动能取代转动动能,化简可得

比较(10)、(19)两式可以得到

此即表示在任意相同的位置,两种情况所对应速度之比为上述结果,结合(15)式,可得两种情况下小球微振动周期之比为

代入(4)式结果即可得到小圆柱质心在其平衡位置附近做微振动的周期和频率为

与原题结果一致．