对“坡角多大,圆柱体在水平面滚得最远”一文的商榷
李 康
(苏州工业园区金鸡湖学校,江苏 苏州 215000)
文献[1]刊登了“坡角多大,圆柱体在水平面滚得最远”一文.原文作者针对苏教版4年级《数学》上册“综合与实践”(同一圆柱体从固定长度的斜面顶端自由滚下,探究坡角分别为30°、45°及60°时,圆柱体在水平面上滚动的距离),[2]先后基于以下6个观点(节选),从理论角度验证教科书中实验结论(坡角为45°时,圆柱体在水平面上滚动的距离最长)的可靠性.
观点1:不考虑斜面的摩擦力,圆柱体沿斜面运动时,同时具有平动动能和转动动能.
观点2:到达水平地面的圆柱体,其动能因克服地面的摩擦力做功转化为内能,故同一圆柱体滚动的距离取决于它在水平面的初速度.
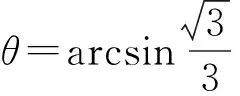
观点4:不论质量怎样均匀分布,圆柱体滚动距离最远的坡角θ=35°保持不变.
观点5:若圆柱体滚动时受到斜面摩擦,虽然滑动摩擦做功,但坡角θ=35°保持不变.
观点6:考虑空气阻力时,滚动距离最远的坡角θ>35°,即实验探究所得结论正确.
笔者认为,以上观点和逻辑论证值得商榷,现从以下4个角度展开分析,供大家评判.
1 斜面上的动力学分析
1.1 不考虑斜面的摩擦力
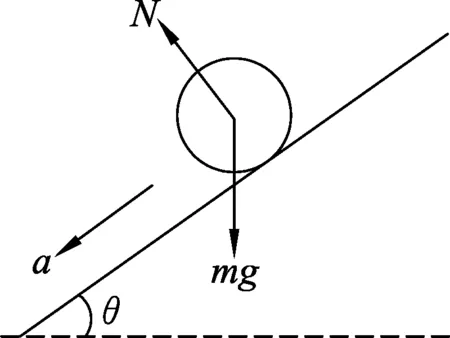
图1
受力分析如图1,圆柱体沿斜面运动时受重力mg和支持力N的作用,即圆柱体质心沿斜面做匀加速直线运动,但各力对质心的力矩均为0,因此,圆柱体的角加速度为0,在下滑过程中只发生平动不发生转动(观点1错误).正是由于摩擦力的存在,圆柱体才能滚动起来,而原文中的推导都是在滚动情况下讨论的,故斜面的摩擦力不能不考虑.
1.2 考虑斜面的摩擦力

图2
1.2.1 圆柱体做纯滚动
受力分析如图2,圆柱体沿斜面运动时受重力mg、支持力N和摩擦力f的作用,设圆柱体的半径为R,其质心沿斜面向下运动的加速度为a,圆柱体绕质心转动的角加速度为β.根据质心运动定理有
mgsinθ-f=ma.
(1)
由于圆柱体绕质心转动,根据转动定律有
fR=Iβ,
(2)

a=βR.
(3)
由(1)-(3)式可得

由(6)式可知,圆柱体所受的摩擦力仅与坡角θ、质量分布k有关,而与接触面的情况无关,这是因为做纯滚动时,接触点速度为0,圆柱体与斜面之间的摩擦力实际上是静摩擦力.设最大静摩擦力fm等于滑动摩擦力,则
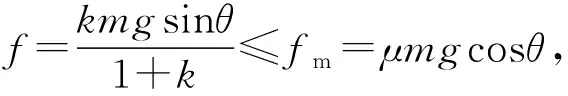
(8)式即圆柱体在斜面上做纯滚动的条件.
由(7)式可得圆柱体与水平地面发生碰撞前的质心速度为(假设圆柱体尺寸远小于斜面长度L)
当然,(9)式也可从能量角度直接得到.由于圆柱体做纯滚动,接触点速度始终为0,静摩擦力的瞬时功率始终为0,故静摩擦力不做功(观点5错误),重力势能全部转化为平动动能和转动动能,有
将纯滚动条件v=ωR带入(10)式可得(9)式.
1.2.2 圆柱体做滚滑运动
若(8)式不能成立,圆柱体沿斜面将做既滚又滑的滚滑运动,接触处的摩擦力变为滑动摩擦力,因此,重力势能不仅转化为动能,还有一部分转化为内能Q,仿照(10)式有
由于滑动摩擦力做功与坡角θ有关,故(11)式求得的速度v(θ)函数关系比(10)式复杂得多,后续求极值也就不同,因此,对应滚动距离最远的坡角会发生改变(观点5错误).为了讨论的方便,本文只考虑纯滚动情形.
2 碰撞时的动力学分析
原文中,圆柱体与地面碰撞瞬间,转动动能及水平向前的平动动能没有损耗,而竖直向下的平动动能全部转化为内能,即图3中分速度vx和角速度ω保持不变,分速度vy消失.如此一来,碰撞后质心速度vx=vcosθ<ωR=v,即圆柱体与水平地面的接触点速度不为0,该点相对地面速度向后,因此,圆柱体在接触处受到向前的滑动摩擦力,直至达到纯滚动状态(观点3错误).
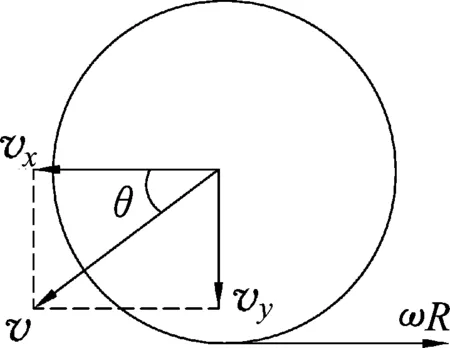
图3图4
受力分析如图4,根据动量定理有
fΔt=m(v0-vx).
(12)
由于滑动摩擦力对圆柱体质心有力矩,根据动量矩定理有
联立(9)、(12)和(13)式可得
3 滚最远的坡角理论值
当圆柱体在水平地面上达到纯滚动状态时,受到重力、支持力和静摩擦力的作用,但3个力都不做功,因此,圆柱体的动能并非克服静摩擦力做功消耗,而是滚动摩擦阻力偶矩做了功,它才最终停下来(观点2错误).根据古典滚动摩擦定律定义的滚动摩擦因数μr,有Ek=μrmgs,代入(15)式得

由(17)式可知,在水平地面上滚最远的坡角θ与质量分布k有关,对不同的圆柱体有k∈(0,1],坡角θ∈(35°,48°](观点4错误).特别地,薄壁圆柱壳k=1,θ=48°;均质实心圆柱体k=0.5,θ=42°.
4 实验与理论对比分析
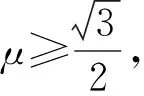
如图5是利用薄壁圆柱壳、实心圆柱体(用密度相近的橡皮泥填充中空部分,k≈0.5)实验数据拟合的s-θ图像.由图可见,在水平地面上滚动最远距离的坡角θ会随着k值的变化而变化.当然,薄壁圆柱壳的坡角实验值接近理论值48°,而实心圆柱体的坡角实验值接近44°,与理论值42°存在一定偏差,这是内部填充材料的密度不能保证和PVC完全相同所致.
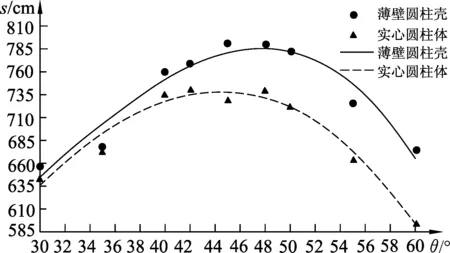
图5
如图6是f(θ)随θ变化的函数图像,比较图5和图6发现,对于薄壁圆柱壳,当坡角小于50°时,两图变化趋势较吻合.当坡角过大时,滚动距离s比f(θ)减小更快,这是因为(16)式中的滚动摩擦系数μr不仅与材料性质和表面状况有关,现代摩擦学理论认为它还与弹性滞后损耗、法向载荷及圆柱体几何尺寸有关;另一方面,坡角越大,圆柱体沿斜面运动速度越大,空气阻力的影响就不能忽略不计,因此,滚动距离随坡角的增大而减小更快(但空气阻力对滚动最远距离的坡角影响不大,不能验证“考虑空气阻力后,坡角应取45°”的实验结论,观点6错误).对于实心圆柱体,由于滚最远距离的坡角实验值比理论值要大,即k值大于0.5,因此,s-θ图像比f(θ)更偏上.

图6
综上所述,原文中的观点1、3、4错在刚体模型与质点模型的混淆,观点2、5错在摩擦的类型及作用判断不清,观点6的提出并未理论证明,且与实验结果矛盾.以上是笔者在阅读原文后提出的不同观点,供大家参考,不当之处请指正.

