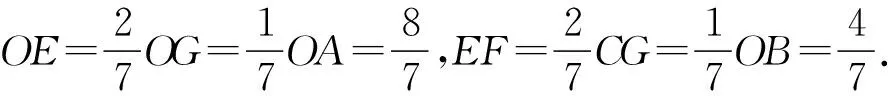运用杠杆平衡条件,确定剩余部分重心

王伟民 辛存良

(1. 安徽省太和县宫集镇中心学校,安徽 太和 236652； 2. 山东省阳谷县西湖中学，山东 阳谷 252311)

重心是重力在物体上的等效作用点．质量分布均匀,外形规则物体的重心在它的几何中心．在规则几何体上挖去一个外形规则的部分,如果挖去部分的重心与原物体重心不重合的话,剩余物体的重心将偏离原来重心的位置．那么,如何确定剩余部分重心的位置呢?

例1.如图1所示,质量均匀的圆盘,半径为R,在圆盘上挖去一个半径为r的圆孔,已知圆孔圆心与圆盘圆心之间的距离为d,若R=kr(k>1),确定剩余部分的重心位置?

分析:如果将挖去的部分重新补上,则补齐后的图形重心在大圆面的圆心,如图2,在此情况下,将大圆面看作是两部分的组合——半径为r的小圆面跟从大圆面上挖去小圆后所剩“偏圆环”图形的组合,由于对称,“偏圆环”图形的重心一定在两圆的连心线上,并且在图2中大圆面圆心O的右侧．如果从大圆的圆心处吊起来,并将大圆的圆心视为支点的话,那么这两部分的重力关于支点平衡,利用杠杆的平衡条件可以确定“偏圆环”(即图1中的阴影部分)图形重心的位置．

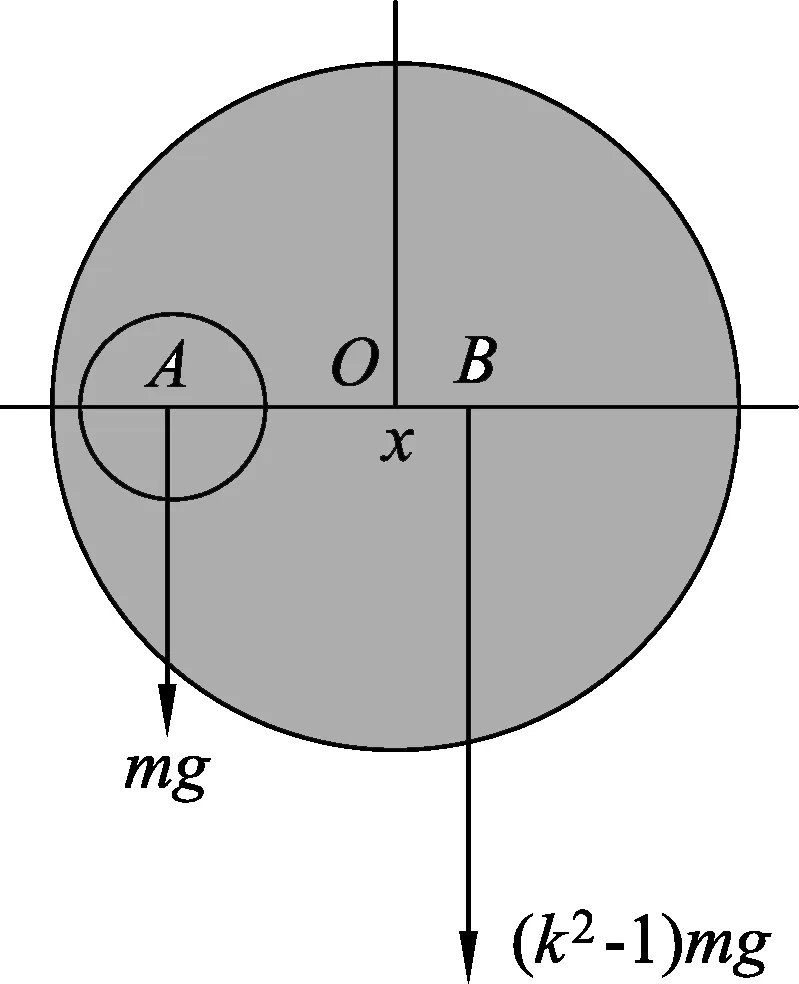
图2

解析:如图2所示,挖去小圆后,剩余部分的重心在两圆的连心线上大圆圆心O的右侧B位置,设OB=x,因为R=kr,所以,大圆面积是小圆面积的k2倍,故“偏圆环”图形的面积是小圆面积的(k2-1)倍,“偏圆环”图形的质量是小圆质量的(k2-1)倍.若设小圆的质量为m,则“偏圆环”图形的质量为(k2-1)m,以O为支点,由杠杆平衡条件得

mg·d=(k2-1)mg·x，

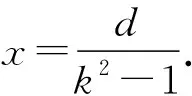
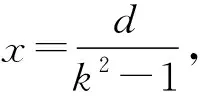
求解挖去一部分之后的平面图形的重心位置时,将原图形看作挖去部分与剩余部分的组合,利用杠杆平衡条件进行求解,方便而又快捷．实际上,这种方法不仅适合于圆形薄片挖去一部分之后,剩余部分重心位置确定的问题,对于其他形状的物体挖去一部分图形之后,剩余部分重心位置确定的问题,也同样适用．

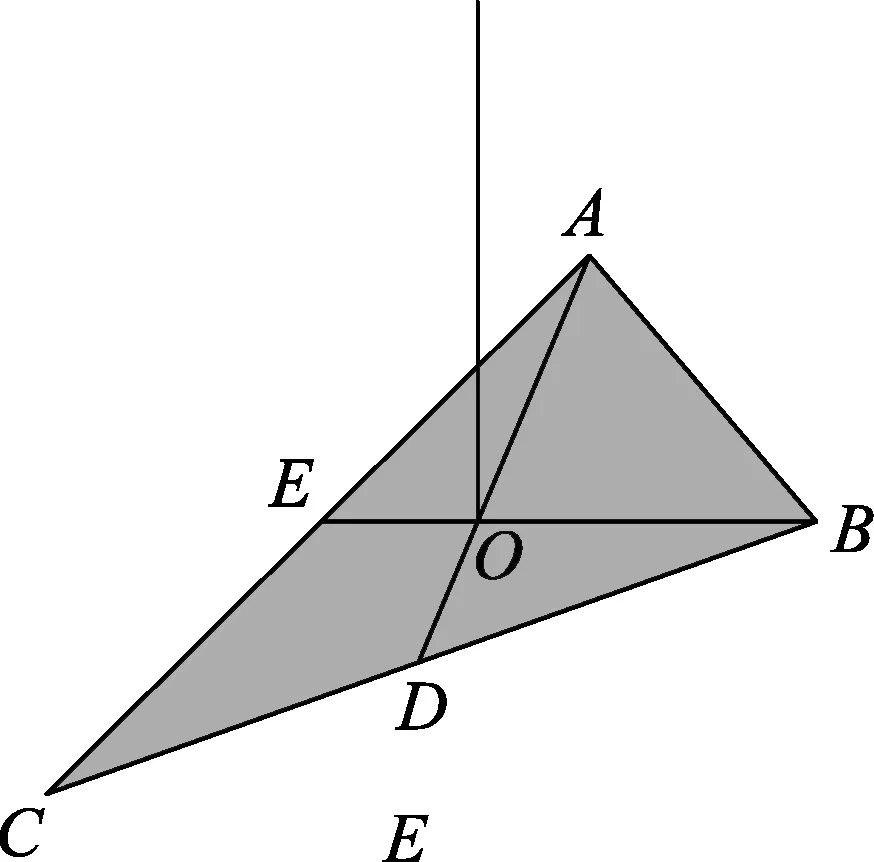
图3

例2.如图3所示,质量均匀的薄片△ABC,O是两条中线AD、BE的交点(即△ABC的重心).过O分别作OG∥AB,OF∥BC,分别交AC于G和F,如图4,若中线长BE=18 cm,将△OFG挖去后,试确定剩余部分的重心位置．

解析:从△ABC的重心O点用细线将其吊起,并让中线BE恰好处于水平状态(这样做便于求解),由相似三角形面积比等于相似比的平方,结合三角形的重心定理容易推出,图4中挖去的△OFG与△ABC面积比为1∶9,所以,剩余部分的质量是挖去部分三角形质量的8倍．如图5所示,由几何知识易知,OE是△OFG的FG边的中线,所以,△OFG被中线OE分成的两个小三角形的重心到OE的距离相等,因此,挖去△OFG之后,剩余部分的重心只是沿△ABC的水平中线BE向右平移,设平移后的重心(即剩余部分的重心)位置N与O间的距离NO=x,因为△OFG的重心M到其顶点O的距离为

由杠杆平衡条件得

mg·OM=8mg·x.

解得x=0.5 cm.

答:剩余部分的重心在中线BE上O点右侧,距离O点0.5 cm处．

图4 图5

图6

例3.在如图6所示的坐标系中,质量均匀的椭圆形薄片,其长半轴和短半轴长度分别为12 cm和6 cm,在薄片上长轴和短轴的一端分别挖去两个与薄片相似的椭圆形孔洞,若挖去的图形与原薄片的相似比为1∶3,试确定剩余部分重心的坐标．

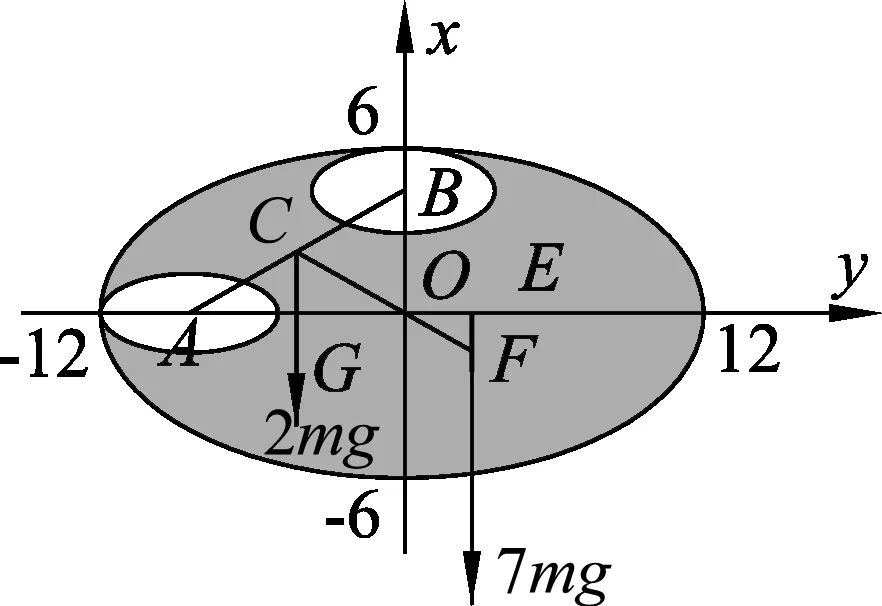
图7

解析:因为相似图形面积之比等于相似比的平方,所以,挖去的一个小椭圆的面积与原来椭圆面积之比为1∶9,因此,如果一个小椭圆薄片的质量为m,那么,挖去两个椭圆孔洞之后,剩余部分的质量为7m．如图7所示,设两个孔洞椭圆薄片的重心分别为A和B,挖去两个椭圆薄片之后剩余部分的重心为F,则未挖去孔洞之前,两个小椭圆的重心在AB的中点C,显然,C、O、F三点共线,以坐标原点0为支点,由杠杆平衡条件得

2mg·OG=7mg·OE.

可得OG∶OE=7∶2.