网络侧评估用户视频体验建模分析

陈 坚

（大连海事大学， 辽宁 大连 116085）

1 研究背景

随着信息化时代的到来，越来越多用户选择在移动智能终端（基于TCP的视频传输及播放）观看网络视频，因此，用户体验成为媒体企业能否胜出的关键要素之一。而影响用户体验的两个关键指标是初始缓冲等待时间和在视频播放过程中的卡顿缓冲时间。

研究表明，初始缓冲时延和卡顿时长占比主要受到初始缓冲峰值速率、播放阶段平均下载速率、端到端环回时间（TE2E，RT），以及视频参数的影响。不过这些因素和初始缓冲时延、卡顿时长占比之间的关系并不明确。

本文在已有实验数据的基础上，建立用户体验评价变量（初始缓冲时延，卡顿时长占比）与网络侧变量（初始缓冲峰值速率，播放阶段平均下载速率，TE2E，RT）之间的函数关系，并在此基础上进行数据检验，对缓冲得分、卡顿得分和VMOS进行深入探究，从而得出卡顿占比与卡顿得分，初始缓存得分与缓存得分的关系，使该模型具有一定的应用价值。

2 初始缓存时延模型与建立

2.1 初始缓存时延模型的求解与建立

分析初始缓冲时延，首先需要明确初始缓存阶段包含的各个阶段。初始缓存阶段主要包含了视频解析阶段、Speedvideo内部准备阶段（TCP慢启动阶段）和下载数据缓存阶段3个子阶段。其中，视频解析阶段过程与Speedvideo内部准备阶段中的TCP慢启动通常包含了数倍的TE2E，RT。

参考时间公式：

可知初始缓冲时延由初始缓存阶段所需要的缓存数据量与初始缓存阶段时长所决定。其中，设初始缓冲阶段需要下载的数据量为D，设码率为Bit，由基于移动视频的移动承载网络要求白皮书[1]可得：

设初始缓冲峰值速率为VM，即在视频初始缓冲数据量阶段下载所需时间为：

设视频解析阶段与Speedvideo内部准备阶段一共经历Ts倍的TE2E，RT，而下载这些数据时间通常不算在视频初始缓冲数据量阶段中。

因此，可得出有关初始缓冲时延公式：

2.2 初始缓冲时延模型的插值和拟合

设常数n为视频解析阶段与Speedvideo内部准备阶段所经历的n倍的RTT。公式：

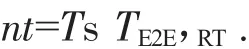
即

令

3 卡顿时长模型与建立

3.1 卡顿时长模型的求解与建立

通过查阅资料可知，当传输速率小于播放速率，并且缓冲区已经清空时，视频发生卡顿现象，其中，卡顿时长占比是严重影响用户体验的变量。因此，本文将该变量的数据和网络侧变量（初始缓冲峰值、播放阶段平均速率和TE2E，RT）进行数据分析，从得到播放阶段平均速率和卡顿时长所拟合出来的数据图像，发现两者间存在强烈相关线性关系[3]。

在对其它变量进行相应的控制后，本文剔除了符合以下条件的数据：卡顿时长为0的无关数据；播放速率过小（v＜1 000）的数据；特殊数据，例如卡顿次数为1或0；离群值，找到大于3倍方差的界限，删除离群值。最终在筛选后的结果得到精确度较高的函数方程式，即卡顿时长方程式为：Tp=-0.003 861x+21.44.

最后根据卡顿时长占比=卡顿时长/播放时长的条件，将Tp的方程式代入，可得卡顿时长（PK）占比公式：

3.2 神经网络模型的求解与建立

人工神经网络是在现代神经科学的基础上提出和发展起来的，旨在反映人脑结构及功能的一种抽象数学模型。本文查阅有关神经网络方法的资料，发现由该方法产生的网络，可用来将相似的样品归于同一类别，因而激发同一输出单元，这一分类方式是网络自身通过学习从输入数据的关系中得出的[4]。

通过建立神经网络模型得到神经元模型以及模型训练效果（见图1），拟合的均值误差在90%以上，符合模型的适用标准[5]。

图1 神经网络模型分析图

其中，x1是代表初始缓冲得分，x2是代表卡顿占比得分。wk1（k=1，2，…10）是对于输入的各隐藏层权值，wk2（k=1，2，…10）是对于输入的各隐藏层权值。f（x）是激活函数，b是阈值，用于激活函数。

本文通过神经网络模型的大量训练，得到各隐藏层的权重后与相应的阈值，其中阈值b=-1.433 3。

将得到的权值与阈值导入本文的神经网络模型之中，就得到相应的初始缓冲得分、卡顿得分与V-MOS之间的关系。

3.3 初始缓冲时延与缓冲得分的关系

通过数据的分析和拟合，发现初始缓冲时延与缓冲得分存在一定的关系，本文对此进行相应的分析得知两者为分段函数关系，接下来将进行分段分析：

1）对于第一段函数范围在（0，10 000），通过matlab的三次方函数拟合，得到相应的函数方程和图像。

2）对于第二段函数，显然其方程为：y=1。

因此，得到初始缓冲时延与缓冲得分间的函数关系式为：

3.4 卡顿占比与卡顿得分的关系

通过数据的分析和拟合，得到卡顿占比与卡顿得分的关系，可知显然两者间存在一定分段线性的关系，本文对此进行相应的分析，并将进行分段分析。得出卡顿占比与卡顿得之间的函数关系为：

4 模型的评价与推广

模型一的拟合是在排除了一定的意外事故后进行的。该模型优点是囊括的大部分数据，且拟合度较高。具有一定的真实性。该模型缺点是并不能做到100%的相似度，有相当多的数据被排除在外。因此，本文需要进一步优化模型得到更为精准的关系。同时，本文将初始缓存阶段设为大约有三个阶段。其中忽略掉了信息交互阶段所求的TE2E，RT，求的是初始缓存阶段总的 TE2E，RT。

本文通过数据的比对，推出一系列的关系。该系列的模型优点是本文还详细计算了卡顿占比得分，缓冲得分与VMOS间的关系，运用神经网络模型，建立更加系统、完备的关系。缺点是该模型忽略了瞬时速率的影响，不能做到更为精准的模型关系。同时其假设条件有一定的限制，使得该模型推广具有一定的局限，但在总体上不影响模型的精准[6]。

本文通过参考相关资料，可以根据建立的模型，求出相应的函数关系，并根据一定的约束条件进行相关的检验，具有一定的实用性。但同时由于现实环境的限制（例如电脑硬件、网络线路具有一定差别等）于假设条件下的限制（例如影响TE2E，RT的因素千差万别等）。因此在具体实践中，还应该对其进行更深层次的模型分析与模型优化，从而使该模型具有更为明显的优势[7]。