一种基于改进的朴素贝叶斯算法的Android钓鱼网站检测方案

2018-08-23 02:58朱二周

计算机工程与科学 2018年8期

马刚，刘锋，朱二周

(安徽大学计算机科学与技术学院，安徽合肥 230601)

1 引言

根据数据显示，2015年中国移动互联网用户数量达到了8.1亿人，较2014年增长了近8.4%。预计到达2016年，中国移动互联网用户数量将达到9.2亿人。从智能手机的用户数量可以看出，我国的移动互联网规模巨大，并在迅速发展中。但是，在移动互联网快速发展的同时，针对移动网络攻击和诈骗的现象时有发生。

网络钓鱼攻击[1]是一种通过模拟正常网站的界面，诱骗用户输入用户名和密码等信息，从而达到盗取用户账号信息的目的。当前，对于PC端的网络钓鱼攻击已经有了较好的防御和保护手段，但针对移动端攻击的检测手段和方法还不是很健全。

当前，对网页钓鱼攻击检测方法的研究主要包括基于黑名单的检测、基于机器学习的检测、基于启发式的检测和基于视觉相似的检测[2]等四类。基于黑名单的检测[2]技术主要根据知名IT企业提供的钓鱼网站黑名单进行检测。基于黑名单的检测技术虽然正确率很高，但是没办法检测不在黑名单内的钓鱼网站。与此同时，由于确认黑名单需要人工验证，故需花费大量的人力和时间等。基于机器学习[3,4]的检测技术主要通过选择钓鱼网站URL的特征，以此来生成训练数据，构造分类器进行检测。在这种方法中，URL特征的选取和分类器的构建是非常关键的因素。基于启发式的检测[2]技术主要根据网站存在的异常特征超出了设定的阈值和不合乎常规的访问等方式来对钓鱼网站进行判断。基于视觉相似的检测[2,3]技术利用钓鱼网站与真实网站的视觉相似超过设定的阈值来进行检测。然而，由于需要复杂的图像处理操作，鉴于现在手机的性能还不能很好地满足此类计算需求，这种方法并不适合移动手机端。

本文通过结合URL链接和网页内容，提出一种基于改进朴素贝叶斯算法[5]的钓鱼网站检测方案。朴素贝叶斯算法由于有着坚实的数学基础和稳定的分类效率，故而在各种分类领域中得到广泛的应用。但是，传统的朴素贝叶斯算法也存在一些不足。针对朴素贝叶斯算法的不足，本文做了如下改进：

(1)在收集样本数据的过程中，属性值缺失的情况时有发生，其中有些信息是无法获取的，有些对象的某个属性是不可用的。也就是说，对于这个对象，该属性值是不存在的。本文将采用K-means算法对缺失的属性值进行填充。

(2)当特征属性的维数过多时，朴素贝叶斯算法就会出现大量条件概率相乘的情况。这些概率值都是小于1的数，而这些趋于零的条件概率相乘，很可能会出现有偏过低估计[6]的情况。本文将概率进行适当放大，以解决结果下溢的问题。

(3)传统的朴素贝叶斯算法认为属性之间是相互独立的，容易忽略属性之间的关联性问题。但是在现实数据中，属性与类别之间都存在或多或少的关联。本文根据属性重要程度的不同对属性进行加权处理，提升朴素贝叶斯算法的分类性能，以此提高钓鱼网站检测的正确率。

(4)在实际情况中，钓鱼网站出现的概率还是比较小的，本文通过调整钓鱼网站与可信网站间的概率比值P，最终选择一个最佳的P值，以此来进一步提高检测的正确率。

本文的实验部署在Android 5.0操作系统上，结果表明，改进后的朴素贝叶斯算法能够有效地检测出手机端的钓鱼攻击，进而可为手机安全运行提供可靠的保护技术。

2 朴素贝叶斯算法的基本原理

贝叶斯算法是以英国数学家Thomas Bayes命名的一种基于概率统计的可能性推理方法[6]，即根据已经发生的事件来预测将来事件可能发生的概率。贝叶斯定理的主要思想为：如果事件发生的可能性不确定，那么量化它的唯一方法就是事件发生的概率。如果事件出现的概率是已知的，那么可以根据数学方法计算出未来事件出现的概率。贝叶斯定理可以用一个数学公式表达，即为贝叶斯定理。具体如式(1)所示：

(1)

其中，P(X)表示事件发生的概率，P(Bi)表示Bi的先验概率。之所以称之为先验概率是因为它的概率不和别的事件有关系。由于P(X|Bi)是根据Bi的概率得到的，因此被称为X的后验概率。简单地说，贝叶斯定理提供了一种基于先验概率计算后验概率的方法。

朴素贝叶斯算法是在贝叶斯算法的基础上通过假定各属性之间不存在任何关联，即属性之间完全独立而得到的一种简化算法[5]。利用朴素贝叶斯算法进行分类的具体过程如下所示：

(1)数据样本集合由一个n维的特征向量T={t1,t2,…,tn}表示，ti(i=1,…,n) 表示数据集合中的一条数据。

(2)实验E的样本空间为S，而B1,B2,…,Bn为S的一个划分，且P(Bi)>0 (i=1,2,…,n)。对于给定的一条待检测的数据项X，分类器将计算X属于每个分类的概率，其中哪个分类的概率最大就将X归为那个分类。P(Bi|X)即为对应类Bi的后验概率。而P(Bi|X)可以根据式(1)来确定。由于P(X)为常数，只需要P(X|Bi)P(Bi)最大，即可判断出数据项X属于哪一个分类。其中类的先验概率可以用P(Bi)=si/s计算，si为训练样本中属于Bi的个数，s为训练样本的总数。

由于朴素贝叶斯算法假定各个属性之间是相互独立的，没有任何的依赖关系，所以有：

(2)

于是朴素贝叶斯公式可以表述为式(3)：

(3)

3 朴素贝叶斯算法的不足及改进

3.1 缺失属性值的填充

3.1.1 缺失数据的现有处理方法

在收集样本数据的过程中，属性值缺失的情况经常会发生。对于缺失数据的填充主要有删除数据和补齐数据两种方式。其中删除数据可能会导致数据发生偏离，从而得出错误的结论。当前补齐数据主要有平均值填充以及使用最可能的值填充等方法。

图1的实验结果显示了使用删除法(菱形线)和平均值法(方形线)改变样本数据中缺失的属性数的正确率。实验中样本数为2 000，钓鱼网站数为500，可信网站数为1 500。从图1中可以看出，由于删除法是直接将缺失数据的数据项去掉，这样虽然可以得到完整的数据集，但是丢失了大量的有价值的数据，导致正确率很低(平均准确率为74.93%)。平均值填充方法是靠属性在其他对象中的取值求平均得到的，但是平均值法只是利用了数据样本中的一个数据项，没有充分利用其它数据项和样本的类别，因此所得到的平均值并不是非常准确(平均准确率为80.52%)。

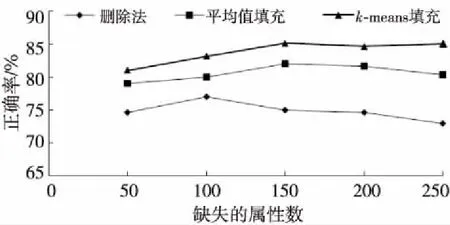
Figure 1 Accuracy comparison vs. missing attribute by different methods图1 不同方法关于缺失属性正确率的对比

3.1.2 基于K-means算法的数据填充方法

由于删除法和平均值法都不能得到最符合实际情况的数据值，本文采用K-means算法来对缺失的数据进行填充。

(1)K-means算法基本原理。

K-means算法[7]是划分聚类方法中一种典型的算法。该算法的目标是根据输入的参数K，将给定的数据集分为K个簇，同一个簇内的数据具有较高的相似度，而不同簇之间的相似度较低。K-means算法的处理过程为：

①从n个数据对象中任意选择K个对象作为初始聚类中心；

②根据每个聚类对象的均值(中心位置)，计算每个对象与中心位置的距离，将它赋给最近的簇；

③重新计算每个聚类的均值(中心位置)；

④循环②～③直到每个聚类不再发生变化为止。

属性对象间相似度的计算：若对象属性均为区间标度度量，则对象之间的相似度最常用的度量方法是欧氏距离，如式(4)所示：

sim(i,j)=

(4)

其中，i=(xi1,xi2,…,xin)和j=(xj1,xj2,…,xjn)分别是两个n维的数据对象。若对象的属性值只有0和1两个状态。则评价两个对象之间的相似度用的是Jaccard系数，如式(5)所示：

(5)

由数学知识可得：

sim(i,j)=(r+s)/(q+r+s)

(6)

其中，r是对于i的值为1而对于j的值为0的变量的个数；s是对于i的值为0而对于j的值为1的变量的个数；q是对于i和j的值都是1的变量的个数。由于本文使用数据的属性值只有两个状态，故使用Jaccard系数计算对象之间的相似度。

(2)使用K-means算法填充缺失数据的具体过程。

针对传统算法对缺失数据处理出现准确率偏低的问题，本文使用K-means算法对缺失数据进行填充，具体过程为：

①原始数据的分离。将原始数据中不完备的数据分离出来，这样原始数据分为两部分：完备数据子集和缺失数据子集。

②完备数据子集聚类。在完备数据子集上使用K-means算法进行聚类，最终产生K个簇。K-means中K值表示的是数据集聚类中心的个数。由于本文的数据集在聚类过程中只有两种类别，一种是钓鱼网站，另外一种是非钓鱼网站(可信网站)，因此这里的K值取2。

③缺失数据填充。计算缺失数据集中的每条记录与K个簇中心的相似度，根据相似度将该条记录划分到相似度最高的一个簇中去，最后用该簇中相应属性出现次数最多的值来补齐缺失的属性值。

④重新计算均值，循环②～④直到所有的缺失数据都填充完毕。

如图1所示，使用K-means算法(三角形线)来对缺失的数据进行补齐的正确率比其它两种方法的正确率都要高(平均准确率达到83.79%),这是因为K-means方法充分利用了当前数据样本中所包含的其它信息，并利用其它属性的值和属性类别来预测当前所缺失的属性值，因此本文使用K-means方法对缺失的属性值进行填充。

3.2 避免有偏的过低估计

对概率进行放大的方法主要有两种。第一种是给每一个sik加上一个比较小的数，这样使得计算出来的概率值较小，也不会占有绝对的统治地位，从而提高了分类的精度，如Laplace平滑方法[5]。Laplace平滑方法是直接在si的基础上加上n(n表示样本类别的种类数)，在sik的基础上加上1。这样可以有效地避免概率为零的情况。第二种方法是基于先验概率估计的方法，即对P(Xk|Bi)的计算先给一个先验的估计概率，然后以此概率为基础对统计的样本数进行放大，如m估计[5]方法。该方法是一种更一般的贝叶斯概率估计方法，它将原来的样本容量添加m个等效的样本，同时样本中增加的等效的类别数量就是样本数量m乘以概率估计E。

图2的实验结果显示了采用Laplace平滑方法(三角形线)和m估计(方形线)的方法对样本数据集进行放大，可以有效地提高正确率。其中，m估计方法由于扩大的样本数量比Laplace平滑方法要大，因此采用m估计方法的正确率比Laplace平滑方法要高。特别地，当样本的数据集很小的时候，m估计方法和其它两个方法的正确率的差值就越大，因为数据集越小，出现零概率事件的概率就越大，从而导致正确率很低。因此，使用m估计对样本数据进行放大，可以进一步提高正确率。

Figure 2 Accuracy comparison among different probability estimation method图2 不同概率估计方法的正确率对比

基于以上分析，本文采取m估计来对样本数据进行放大，计算方法如式(7)所示：

(7)

其中，sik和si与前面的定义相同，E是确定的概率的一个先验估计值，而m是一个放大的样本容量的大小。最终的结果是将n个实际的观察样本进行了放大，加大了m个按E分布的虚拟样本。在这里，假定E是均匀的先验概率，那么，如果某属性有k个可能的值，那么就设置E=1/k。

3.3 属性加权

传统的朴素贝叶斯算法为了降低算法的复杂度，直接忽略了属性之间的关联。但是，在现实情况中，属性与类别之间都存在或多或少的关联，如果不考虑属性之间的关联，就会使得分类的效果明显下降。Tan等人[8]提出了加权朴素贝叶斯模型，该模型根据属性和最终所属的类别之间的关系赋予不同的权重，这种方法简单有效。因此，本文使用加权朴素贝叶斯方法对属性与类别之间的相应关系进行量化，并以该量化值作为加权系数对该属性进行加权，以此来提高朴素贝叶斯算法的分类效果。在这种情况下，关联程度较大的属性将获得比较大的加权系数，而关联程度较小的属性将获得比较小的加权系数。

根据以上分析，可得加权后的朴素贝叶斯公式如式(8)所示：

(8)

其中，wi为数据中第i个属性对于样本的权重，属性的权重越大，说明该属性对分类的影响越大。加权朴素贝叶斯算法的关键问题在于如何确定不同属性对于样本的加权值。首先定义：

(9)

其中,count(Bi)表示样本数据中类别为Bi的个数，count(Bi∧Xk)表示数据中类别是Bi且第k个属性值为Xk的个数。根据数学知识很容易定义权重wi为：

(10)

由于P(Xk|Bi)为小数，由数学知识可得，需要把权值wi取倒数。

3.4 K值估计

利用前面的朴素贝叶斯公式(式(3))可以计算出每一个待分类网站X属于钓鱼网站和可信网站的概率：P(B1|X)(B1为钓鱼网站类别)和P(B2|X)(B2为可信网站类别)。如果按照传统的方法，当P(B1|X)>P(B2|X)时，就判定X属于钓鱼网站，否则就判定为可信网站。但是在实际的情况中，正常网站的数量往往比钓鱼网站的数量多很多，传统的朴素贝叶斯算法就会产生较高的误判率，如果直接使用的话，分类的偏差会比较大。因此，为了能更加准确地检测出钓鱼网站，减少检测过程中的误判率，需要对朴素贝叶斯算法进行改进。

改进的朴素贝叶斯算法的基本思想是：在比较两个分类P(Bi|X)的概率时设定一个阈值P[9]：若第一类除以第二类的结果大于P时，表明X属于第一类的概率远大于属于第二类的概率，即将待检测的网站归为第一类；否则将它归为第二类。其中P值越大，待检测网站属于第一类的可能性也就越大。

我们定义P1表示X属于钓鱼网站的概率，P2表示X属于可信网站的概率。当P(B1|X)/P(B2|X)>P(P>0)时，就判定X为钓鱼网站，否则就判定为可信网站。即当一个待检测的网站为钓鱼网站的概率是可信网站概率的P倍时，就将其判定为钓鱼网站。P越大，其为钓鱼网站的可能性就越大。P的取值是通过大量实验最终确定的。

4 基于改进的朴素贝叶斯算法的防钓鱼方案

4.1 方案的具体实现

本文提出的移动平台钓鱼网站检测方法的大致流程为：首先，从用户访问的URL入手，当手机端用户通过浏览器输入URL加载网页的时候，开始提取URL的4个特性属性[10]，即URL中是否包含IP地址、URL中是否包含‘_’‘@’等异常字符、URL是否具有多级域名以及URL的字符长度是否过长。其次，通过URL获取网页内容(HTML源码)，同时提取网页内容的4个特性属性，即否包含‘form’表单、是否包含‘username’关键字、是否包含‘password’关键字以及是否存在外部链接。最后，将提取到的8个特征属性组成一个特征向量[5]，利用改进的朴素贝叶斯方法进行检测，如果是钓鱼网站，就向用户发出警告。具体的检测过程如图3所示。

Figure 3 Flow chart of phishing site detection图3 钓鱼网站检测流程

4.2 特征向量的构建

钓鱼网站通常为了迷惑用户，将网站的URL和网页内容进行了伪装[7,11]。根据总结和归纳钓鱼网站的特点，本文从中提取了钓鱼网站的8个特性，将这些特性组成特征向量(V)[12 - 14]。特征向量的具体定义为：V=〈v1,v2,v3,v4,v5,v6,v7,v8〉,V中各个分量的具体含义为：

(1)v1：URL中是否包含IP地址[15,16]。攻击者经常用IP地址作为网站的URL来迷惑用户，而这样的URL极有可能是恶意的钓鱼网站。

(2)v2：网站的URL中是否包含‘_’‘@’等异常字符。钓鱼网站通常用添加特殊字符的方法来迷惑用户。

(3)v3：URL是否具有多级域名。当网站域名过长时，大部分用户往往会忽视URL后半部分的内容，而很多钓鱼网站通过多级域名来达到迷惑用户的目的。本文通过检测URL中是否含有大于5个‘.’来判断该URL是否包含多级域名。

(4)v4：URL的字符长度是否大于30。一般可信网站的长度都不会太长，如果URL的长度过长，极有可能是钓鱼网站。

(5)v5：网页内容中是否包含‘form’表单。‘form’表单是用来提交用户信息的，存在‘form’表单，说明网页需要用户填写信息，用户需要特别注意。

(6)v6：网页内容中是否包含‘username’关键字。‘username’在网页源代码中通常表示用户的登录ID，如果存在，极有可能是攻击者想要获取用户的ID。

(7)v7：网页内容中是否包含‘password’关键字。‘password’在网页源代码中通常代表用户的登录密码，如果存在，很有可能是攻击者想要窃取用户的登录密码。

(8)v8：是否存在外部链接。网页中存在外部链接是正常的，但是如果网页中外部链接的数量过多(这里指外部链接的数量超过20个)，这个网页很有可能是可疑的，用户需要特别注意。

5 实验

5.1 实验数据

由于钓鱼网站的存活周期短，实验以实时收集的网站信息作为测试用例。实验所用的钓鱼网站是从安全联盟网[17]上获取的，可信网站是从Alexa[18]网站上获取的。实验随机抽取了数据集的1/2用作训练，余下1/2用作测试。

5.2 实验平台

实验部署在Android平台(基于Android 5.0的系统)，手机的内存为2 GB，编程环境为Eclipse，JDK版本为1.7.0_79。测试算法性能的实验环境是一台拥有4 GB内存和双核i3处理器的PC机，运行Windows 7操作系统和Eclipse，JDK版本为1.7.0_79。

5.3 实验结果评估标准

实验通过验证结果的正确率(Y)、精确率(Q)和召回率(R)[12]等几个方面来分析改进后算法的性能。正确率、精确率和召回率是广泛用于信息检索和统计学分类领域的三个度量值，用于评价结果的质量。其中，正确率反映的是被分类器判定为正确的检查结果占所有样本的比重；精确率反映的是被分类器判定为正例中真正的正例样本的比重；召回率反映的是正例中被分类器判断为正例的比重。Y、Q、R的具体定义如下：

Y=(A+D) / (A+B+C+D)

(11)

Q=A/ (A+B)

(12)

R=A/ (A+C)

(13)

其中A、B、C、D的含义和关系如表1所示。

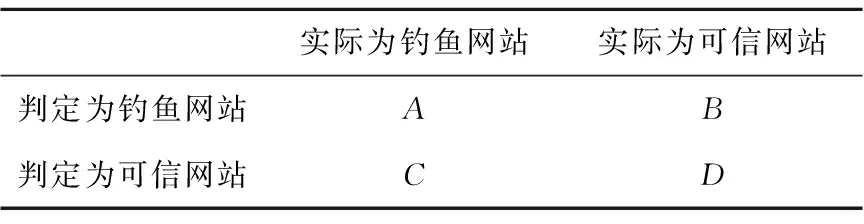
Table 1 Definition of parameter A,B,C and D

5.4 实验结果及分析

(1)P值的确定。

实验首先需要寻找一个固定的概率比值P。实际应用中需要通过大量的实验才能确定较为合适的P值。在实验过程中往往要根据所研究的具体问题，适当估算P的取值范围。

本文实验中设定比值P的初始值为0.1，并按步长为0.1逐步增加。从测试数据集中选取了500个URL，其中包括300个可信网站和200个钓鱼网站。图4显示了随着比值P的增加，实验正确率的变化情况。

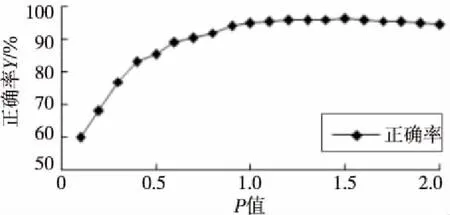
Figure 4 Relationship between P and Y图4 正确率Y随着P值的变化

经过大量的实验发现，当P=1.5时，可信网站被误判为钓鱼网站的概率最低。同时，钓鱼网站被误判成可信网站的数量也是最少的。由此可见，当P=1.5时，系统的正确率是最高的。在此，只列出当P=1.5时的实验数据,如表2所示。

Table 2 Experiment results when P=1.5

(2)实验结果。

为了测试改进后的算法在不同数据集中的性能，实验对数据集进行采样，测试不同大小数据集在相同环境下的正确率、精确率和召回率。

实验从测试数据集中选取了8组数据作为样本。第1组实验总共选取了500个URL，其中可信URL数量为300个，钓鱼URL为200个；第2组实验总共选取了1 000个URL，其中可信URL为600个，钓鱼URL为400个；第3组实验总共选取了1 500个URL，其中可信URL为1 000个，钓鱼URL为500个；第4组实验总共选取了2 000个URL，其中可信URL为1 200个，钓鱼URL为800个；第5组实验总共选取了2 500个URL，其中可信URL为1 500个，钓鱼URL为1 000个；第6组实验总共选取了3 000个URL，其中可信URL为2 000个，钓鱼URL为1 000个；第7组实验总共选取了3 500个URL，其中可信URL为2 500个，钓鱼URL为1 000个；第8组实验总共选取了4 000个URL，其中可信URL为2 500个，钓鱼URL为1 500个。

分别对改进前的朴素贝叶斯方法、改进后的朴素贝叶斯方法以及主流的基于决策树的分类方法[4]在召回率、精确率和正确率等方面进行对比。

如图5～图7所示，改进后的朴素贝叶斯方法在正确率、精确率和召回率等方面的指标比未改进的方法有大约10%的提高。和主流的基于决策树分类器相比，改进后的朴素贝叶斯方法的精确率、召回率都比基于决策树的分类器要高。在正确率方面，只有当样本数据为1 000时，基于决策树的分类方法才高于改进后的朴素贝叶斯方法；在其余样本点数情况下，改进后的朴素贝叶斯方法的正确率都要比基于决策树的分类方法的正确率高；以此同时，随着样本数据的增大，两者正确率的差值也会越来越大，这是因为朴素贝叶斯方法非常依赖于样本数据集，样本数据集越大，它在计算概率的时候就越准确。当测试数据达到3 000时，系统检测的正确率达到了97.32%。因此，当用户使用浏览器进行网络访问时，可以对手机的安全性进行很好的保护。

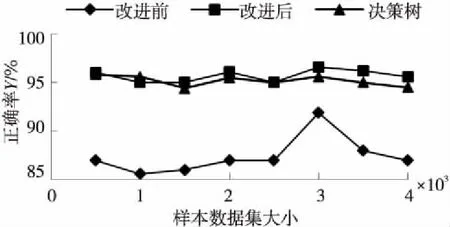
Figure 5 Comparison of Y图5 正确率对比

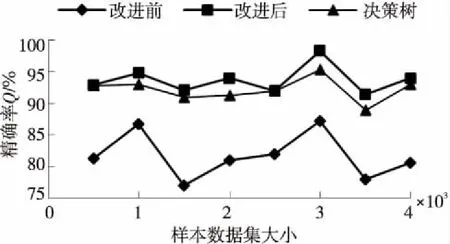
Figure 6 Comparison of Q图6 精确率对比

Figure 7 Comparison of R图7 召回率对比

方案的运行结果如图8所示。当用户输入钓鱼网站的URL时，系统会很快检测出来，并用提示框的形式提醒用户。

Figure 8 Experiment of phishing site detection图8 钓鱼网站检测实验

以下实验比较不同方案之间检测效果的差异。实验的样本数为2 000，其中钓鱼网站数为500，可信网站数为1 500。其中，基于决策树的方案[4]是根据使用树形结构对网站的特征属性进行分类的。基于属性加权的分类器是对数据样本的属性进行加权处理来对钓鱼网站进行检测[8]。基于贝叶斯和支持向量机的分类器是将URL和网页内容分别用贝叶斯和支持向量机进行分类[19]。表3展示了不同方案检测钓鱼网站正确率的对比。

从表3的对照结果可以看出：(1)在正确率上，本文提出的改进的朴素贝叶斯方案相比其它三个方案都有不同程度的提高；(2)本文方案的方差也稍低于其它三种方案，说明本文方案的稳定性要好于其它三种方案。与此同时，由于贝叶斯算法在分类消耗时间上有着自身的优势，综合比较可知，本文的方案要优于其它三个方案。

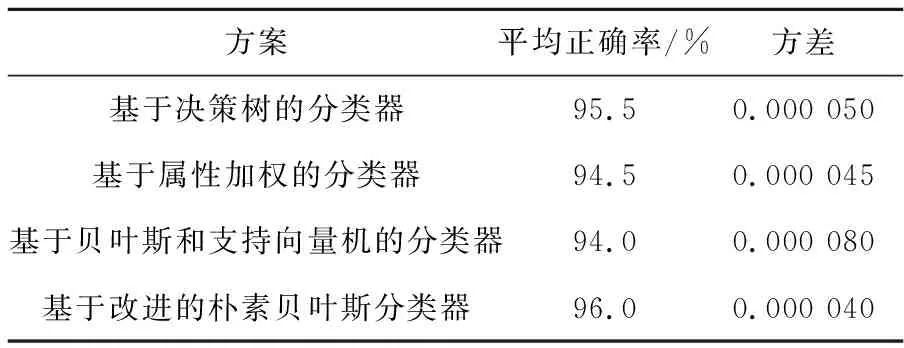
Table 3 Accuracy comparison of different schemes

5.5 检测时间

当用户输入URL开始连接网络时，系统必须在极短的时间内对用户输入的URL做出判断，如果是钓鱼网站，需要及时提醒用户。

反钓鱼方案的检测过程大致可以分为三个阶段：(1)提取URL特征属性；(2)通过URL加载HTML源代码，并提取网页内容的特征属性；(3)通过样本数据得出结果。每个阶段的检测时间如表4所示。从表4可以看出，三个阶段的平均执行时间[20]分别是0.013 s，1.3 s和0.085 s。其中，通过URL加载网页内容并提取特征属性阶段占据了整个检测阶段93%的时间。

三个阶段执行时间的实验结果是取100次结果的平均值，最终检测一次所花费的平均时间为1.398 s。当检测开始时，如果检测的结果是钓鱼网站，系统会用提示框的形式提醒用户。在大多数情况下，在用户输入隐私信息之前，检测的结果就会出来，这对于用户来说是可以接受的。

Table 4 Execution time

6 结束语

本文针对移动平台钓鱼网站频发的现象，提出了一种基于改进朴素贝叶斯算法的方案来检测针对移动端的钓鱼网站。在检测过程中，对于缺失属性值的数据，本文用K-means算法对缺失的值进行填充；针对朴素贝叶斯算法计算概率时会出现过低估计的问题，本文将概率进行放大，解决了结果下溢的问题；针对朴素贝叶斯算法容易忽略属性之间的关联性问题，本文对不同的属性值进行了加权处理，进而提高了检测的正确率；根据实际情况中钓鱼网站出现概率较小的情况，本文通过调整钓鱼网站与可信网站的概率比值，从而进一步提高了检测的正确率。本文实验部署在基于Android 5.0操作系统的手机上，结果表明改进后的算法能够在较短的时间内有效判断出用户需要连接的网站是否是钓鱼网站。

虽然本方案可以有效地判别用户连接的网站是否是钓鱼网站，但是钓鱼网站的更新速度很快，本文所选取的特征属性只有8个，涉及的范围不够全面，所以需要做进一步的改进，以扩大本方案的适用范围。