客车空调冷凝器数值分析与结构优化

章嵩松

(上海加冷松芝汽车空调股份有限公司，上海 201100)

随着客车技术的发展，对客车空调结构设计和性能的要求越来越高［1］。蒸发器和冷凝器是空调的重要组成部分，而空气侧气流分布的均匀性是影响其性能的重要因素之一［2－4］。

关于换热器性能与气流均布性的研究［5－10］有很多，而采用CFD技术已经成为一种重要的手段。本文利用Fluent软件对某客车空调冷凝器的气流分布进行分析，利用风速相对偏差均值作为气流均布性的评价标准，在此基础上提出不同的结构优化方案，以改善芯体的气流均布性。

1 原方案模拟计算

1.1 建立模型

该冷凝器双侧对称，故对冷凝器的一侧建立1∶1的二维模型并进行模拟计算，一方面减小计算量，另一方面有利于结构优化，大大缩短设计周期。在模型简化中，尽量保留对内部流场产生影响的内置构件，如风机壳、芯体支架、导流肋等。简化的冷凝器二维模型如图1所示(图中尺寸单位为mm)，其中风机采用送风的形式，长度为160 mm，出风口半径为810 mm，弧长为390 mm，导流肋与芯体支架间距L=280 mm，导流肋高度h=25 mm，跨度为60 mm，采用管片式芯体，芯体管为6排24列。

图1 简化的冷凝器二维模型图

1.2 网格划分与边界条件

模型采用四边形结构化网格，网格尺寸为2 mm，芯体区域网格进行加密处理，芯体管周围建立5层边界层，层高为0.1 mm，网格总数为89 257个，节点总数为84 307个。风机送风口采用速度进口，均匀送风，风速为7～15 m/s，采用标准κ－ε双方程湍流模型，湍流强度为4%。出风口采用压力出口，表压为0 Pa。芯体管采用wall壁面边界条件。

1.3 模拟结果与分析

在每排相邻芯体管之间提取计算点考察冷凝器内部气流的均布性。计算点布置如图2所示，芯体管排数用N表示，共6排，每排23个计算点，计算点1～8位于芯体上端，计算点9～16位于芯体中端，计算点17～23位于芯体下端。气流均布性的评判标准有多种［11］，本文采用风速相对偏差δi及其均值δ来表示，分别考察不同N下各计算点的风速分布，公式为:

图2 计算点布置图

不同工况下各计算点的风速分布结果如图3所示。图3(a)中，对于大部分计算点，风速的增加会导致相对偏差增大，气流均布性降低。计算点1～4、10～15相对偏差很大，说明芯体上端和中端气流分布很不均匀，上端风速偏小，中端风速偏大;芯体下端各计算点相对偏差较小，说明其风速分布比较均匀。图3(b)中芯体上端计算点1、4、5相对偏差差异性较小，2、3差异性较大，说明芯体上端流场较复杂，风速分布的均匀性较差。

图3(b)中当N=4时，总体上相对偏差均值最大，达到40.0%，结合图3(a)，后续的流场优化方案考察进口风速15 m/s、芯体管N=4条件下各计算点的风速分布。

图4为进口风速15 m/s冷凝器流场速度云图，其中风机壳和导流肋对流场影响较大，风机壳的存在导致芯体上端存在负压区，气流在芯体管周围形成了漩涡，导致风速偏低，管内制冷剂不能得到充分利用，严重影响其换热效率，需要进行优化。导流肋位于冷凝器内部风速较大的区域，迫使气流由芯体下端转向芯体中端。

图3 不同工况下各计算点相对偏差对比

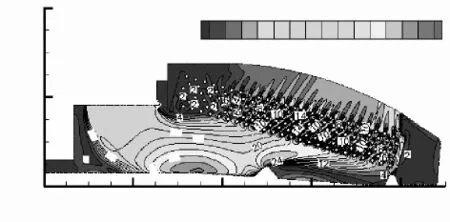
图4 进口风速15 m/s冷凝器流场速度云图

通过对现有结构分析，发现冷凝器芯体气流分布的均匀性较差，需要结构优化改善其气流组织，提高气流分布的均匀性。

2 优化方案一

只对冷凝器底壳部分进行改进，分别考察其导流肋与芯体支架间距L、导流肋的高度h对提升气流均布性的影响。

2.1 改变冷凝器底壳中导流肋的位置

原冷凝器其他参数保持不变，只改变其底壳中导流肋与芯体支架的间距L，分为两种情况:一种是增大，L分别为280 mm(原结构)、320 mm、360 mm、400 mm、440 mm、480 mm、520 mm、560 mm;另一种是减小，L分别为 280 mm、240 mm、200 mm、160 mm、120 mm、80 mm。计算冷凝器内部气流分布情况。

计算结果如图5所示，图5(a)中，当L由280 mm增至480 mm时，芯体上端风速增加，中端风速降低，下端风速基本不变，整体风速均布性提高，当L=440 mm时，相对偏差均值最小，达到25.5%;当L增至480 mm以后，芯体下端风速急剧增加，整体风速均布性降低。图5(b)中，随着L的减小，芯体上端、中端风速减小，下端风速增加，导流肋的导流作用越来越弱，相对偏差均值增大，严重降低了风速分布的均匀性。

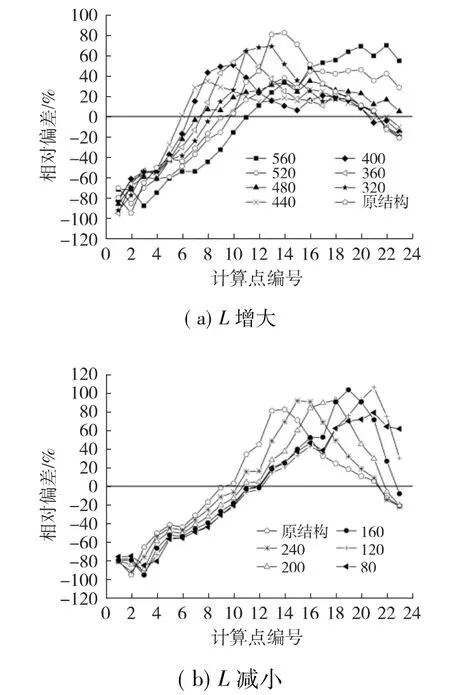
图5 导流肋不同位置气流均布性对比

总结来看，增加L有利于提升气流均布性，当L为440 mm时，气流的均布性最好，相对于原结构，气流均布性提升36.3%。

2.2 改变冷凝器中导流肋的高度

原冷凝器其他参数保持不变，只改变其底壳中导流肋的高度 h，使 h分别为 5 mm、10 mm、15 mm、20 mm、25 mm(原结构)、30 mm、35 mm。计算冷凝器内部气流分布情况。

计算结果如图6所示，当h由25 mm减小至5 mm，芯体上端风速降低，下端风速增加，相对偏差平均值一直增加，气流的均布性降低;当h由25 mm增加至30 mm，芯体中端风速增加，下端风速降低，气流均布性基本不变;当h增加至30 mm以后，芯体中端风速偏大，下端风速偏小，气流均布性降低。与原结构相比，只改变导流肋的高度h对提升气流均布性效果不明显。

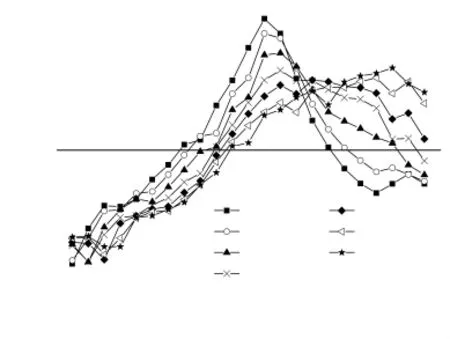
图6 导流肋不同高度气流均布性对比

综上，优化方案一中通过增加导流肋与芯体支架的间距L可以有效提升原冷凝器气流的均布性，当L=440 mm时，效果最佳，而只改变导流肋的高度h对提升气流均布性效果不明显。

3 优化方案二

原冷凝器底壳不变，在风机下方添加导流板，其几何模型如图7所示(图中尺寸单位为mm)，其中导流板由平板和圆弧构成，平板长度为40 mm，圆弧半径为36 mm，平板相对于底壳的高度为H。在原冷凝器和导流板其他参数不变的情况下，只改变导流板的高度H，使H 分别为30 mm、40 mm、50 mm、60 mm、70 mm、80 mm、90 mm。计算冷凝器内部气流分布情况。

图7 导流板模型图

计算结果显示:当H＜50 mm时，芯体中端风速偏大，气流整体均布性较差;当H＞70 mm时，导流板会挡风，导致芯体上端局部风速偏低，气流均布性也会变差;当50 mm≤H≤70 mm，导流板导流作用较好，减弱了原结构中芯体上端风速偏低，中端风速偏高的程度，气流整体的均布性得到了提高，其中，当H=60 mm时，如图8所示，气流均布性最好，相对偏差均值为23.0%，与原结构相比，气流均布性提升了42.5%。

图8 导流板不同高度气流均布性对比

总体来看，优化方案二中添加导流板，可以有效提升原冷凝器气流的均布性，同时，当导流板的高度H=60 mm时，效果最佳。

4 优化方案三

采用正交设计方法对方案一、方案二的结合进行分析，所选因素包括导流肋相对位置L、导流肋的高度h、导流板的高度H。添加导流板后，原冷凝器内部流场改变，导流肋相对位置L和导流肋的高度h的水平范围需要重新计算，所选用的因素与水平见表1。

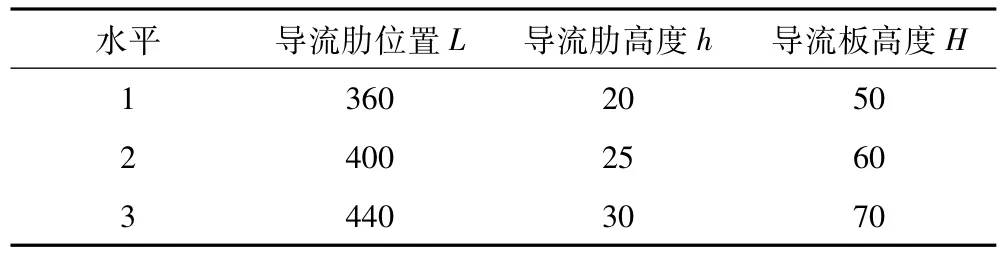
表1 结构优化因素水平表 mm

从表3可以看出，各因素对气流均布的影响程度导流肋高度＞导流板高度＞导流肋位置;从表2相对偏差均值可以看出，提高原冷凝器气流均布的最优方案为实验7，即最佳的结构优化方案是导流肋相对位置L为440 mm、导流肋高度为20 mm、导流板高度为70 mm，此组合下气流分布的相对偏差均值为15.2%，相比较于原冷凝器，气流均布性提高62.0%。

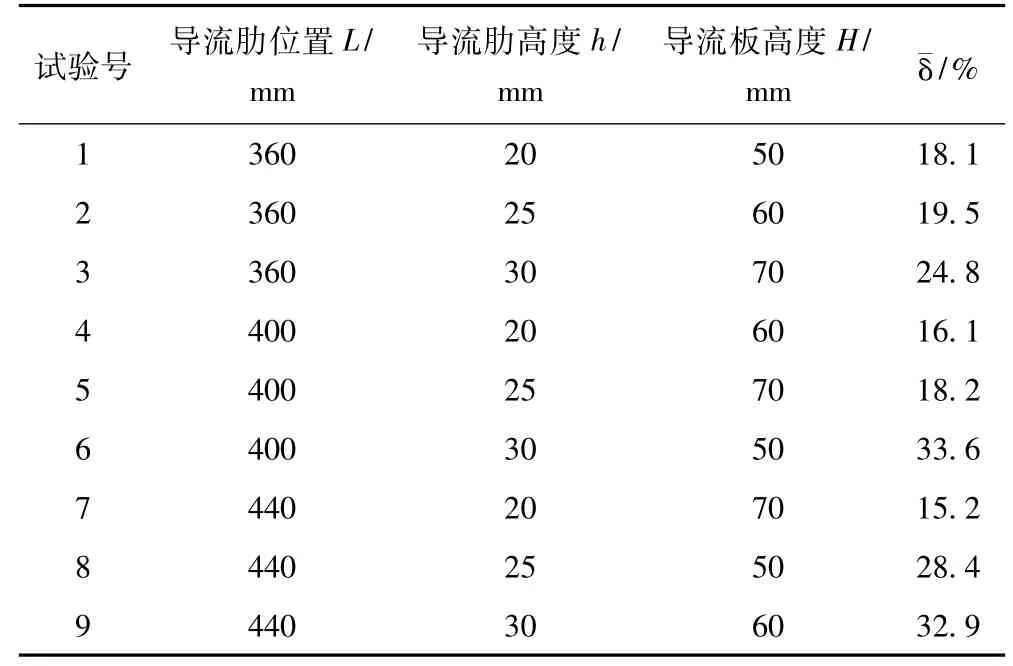
表2 正交实验方案和计算表

表3 试验结果极差分析表 %

5 结束语

通过CFD技术与正交设计方法相结合，对客车空调冷凝器原方案进行了数值分析与结构优化，通过改变导流肋的位置、导流肋的高度以及导流板的高度得到3种方案，其中最佳的优化方案使得风速相对偏差均值由原方案的40.0%降低至15.2%。采用CFD技术与正交设计方法相结合，可以对客车空调冷凝器的多种结构特征进行设计与优化，大大缩短项目的开发周期。

修改稿日期:2018－04－03