车载雷达检测图像自动识别追踪

张 帆

(中铁第四勘察设计院集团有限公司,武汉 430063)

0 引言

隧道病害是困扰铁路发展的关键因素，更是影响国民经济发展的重要因素。隧道围岩长期在线路荷载振动等作用下，会出现隧道衬砌厚度不足等隧道病害。铁路相关部门于1997年对我国铁路隧道状态进行的统计显示，全国运营的铁路隧道有5 000余座，其中发生病害而导致无法正常运营的达到了1 502座，约占运营总隧道的50%[1-2]。据资料记载，成昆线、宝中线、襄渝线、贵昆线、宝成线等都发生过衬砌掉块现象，导致隧道衬砌厚度不足，造成隧道衬砌病害。特别是2001年达成铁路线，其中一隧道出现的拱顶衬砌掉块达到30 m范围，给安全行车带来极大隐患。因此，铁路相关部门每年都对隧道衬砌病害的预防和维护投入大量的人力、物力和资金，但是隧道病害的现象仍然没有得到根本好转[3-4]。

笔者采用车载空气耦合式探地雷达对隧道衬砌进行检测，基于GprMax2D模拟软件并以Matlab为平台环境，建立五种隧道衬砌模型并对其追踪算法进行研究，分析追踪结果，探究位于同一隧道横截面处五种工况下的自动识别追踪方法。

1 原理介绍

1.1 探地雷达波传播原理

图1为车载式铁路探地雷达的探测原理[5]，探地雷达脉冲源产生脉冲电信号，由转换器将电信号转换为电磁波信号，通过发射天线发射出来，电磁波在介质层面进行传播，当介质的介电常数发射变化时，产生反射回波，反射回波由接收天线接收。在同一个测点处，探地雷达接收天线将在瞬间接收到隧道衬砌不同界面反射回来的反射波，每条反射波的波峰或波谷和相应深度的衬砌层面一一对应。每一个完整的波形，称一个扫描线(A-scan)，当测试连续进行时，将每个测点处得到的扫描线重叠到一起，就得到了反射波连续的剖面图，也就是探地雷达图像。探地雷达图像可直观地反映地下结构层面的变化和物性的变化。

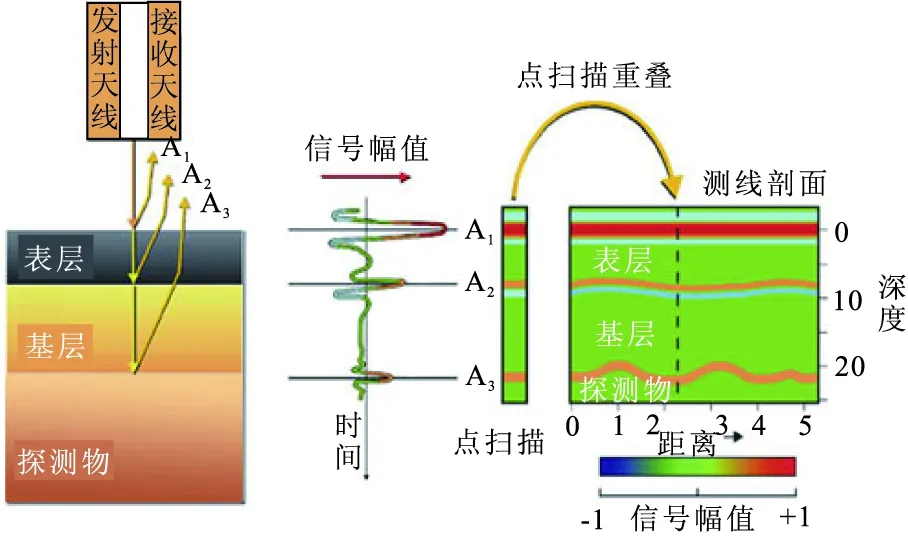
图1 探地雷达探测原理Fig.1 The detection principle of ground penetrating radar

1.2 GprMax2D正演模拟原理

在电磁场计算领域中，由K. S. Yee[6]提出的时域有限差分法(Finite-Difference Time-Domain, FDTD)，是常用的一种方法，常用的麦克斯韦方程(Maxwell's equation)就是其模型基础。随着电子计算机技术的快速发展，时域有限差分法快速发展，被广泛应用于电子学，电磁学，光学等领域。

麦克斯韦方程可用来表示宏观中全部的电磁现象，电磁场量间的数学关系通常用如下偏微分方程进行描述：

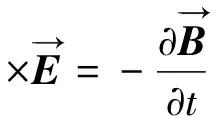
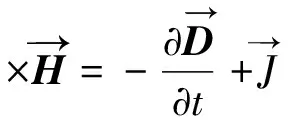
(1)

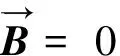
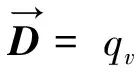
其中:t为时间，s；qv为电荷密度，C/m3；B为磁感应强度，Wb/m2；D为点位移矢量,C/m2；H为磁场强度,A/m；E为电场强度,F/m；J为电流密度,A/m2。方程中的所有向量都是连续、无界的。

空间离散Δx、Δy和时间离散Δt的取值大小，对时域有限差分模型的网格划分有很大影响，它们取值较小时，模型就会比较精确，但运行量会较大。因此，要同时兼顾模型的精度和运行速度，确定适量的时间步长Δx、Δy，来得到满意的结果。Δt可以通过公式(2)确定。

(2)

其中:c为光速。

探地雷达是通过电磁波对有限领域内的目标进行探测得到反射波，经过计算得到目标的距离来确定目标位置的，因此，在模型中需要对探测范围的边界条件要进行假设，即吸收边界条件(ABC)，来模拟无界的空间。吸收边界条件的作用是吸收边界处的电磁波能量，以达到无界空间的要求[7-8]。

1.3 自动识别追踪原理

笔者对铁路隧道衬砌层位自动识别追踪进行模拟研究。对模拟得到的探地雷达数据进行数据处理，并分析总结隧道衬砌层位特征，根据反射波的波谷或波峰出现的时间和相应深度的衬砌层面一一对应的波形特征，利用Matlab编程找到初衬和二衬的分界层，对层位及病害进行自动追踪，研究隧道衬砌及病害层位自动追踪算法，实现自动解译，并在剖面图中显示出来，从而达到隧道衬砌层位自动追踪的目的。

2 层位自动识别追踪

隧道结构的组成，从外向里依次为二衬、初衬、围岩，为了便于模拟计算，在模型中每层介质的介电常数和电导率都是恒定的，根据实际介质的介电常数和电导率的大小，在模型中每层介质的取值如下：

由于模型采用的是空气耦合式探地雷达，雷达和隧道之间有一定的距离，所以第一层为隧道中的空气，取其相对介电常数为“1”，电导率取为“0”；第二层为二衬，其组成材料是混凝土，根据隧道设计规范，取其相对介电常数为9，电导率取为0.03；第三层为初衬，其组成材料也是混凝土，但是和第二层相比，它们的介电常数和电导率不同，取其相对介电常数为4，电导率取为0.02；如果病害层含有水介质，取其相对介电常数为81，电导率取为0.01。模型中探地雷达的参数根据实际雷达情况，设置如下：雷达波的脉冲频率为900 MHz，时窗为30 ns，雷达发射和接收天线之间的距离为2 cm，离散模型的网格大小为0.1 cm。

结合隧道衬砌病害的实际情况，分别建立正常以及含有病害的隧道衬砌模型，各个模型除了介质不同外，其他参数都相同，对模拟得到的数据经过数据处理后[9]，通过隧道衬砌层位识别特征[10]，编写程序自动识别追踪隧道衬砌及病害结构的分界层[11]，得出最终自动识别追踪结果。正演模型参数如表1所示。

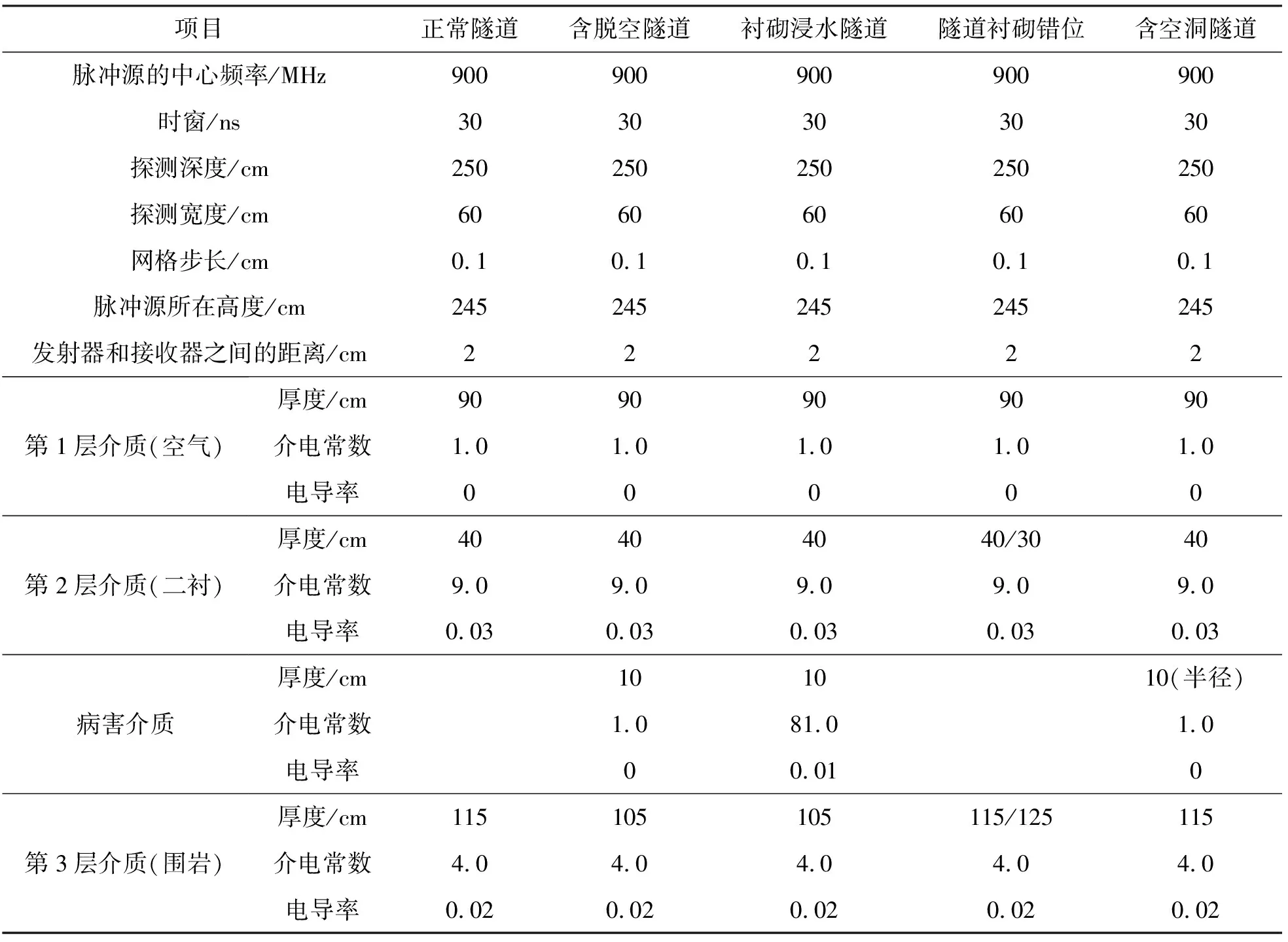
表1 隧道衬砌模型建模参数

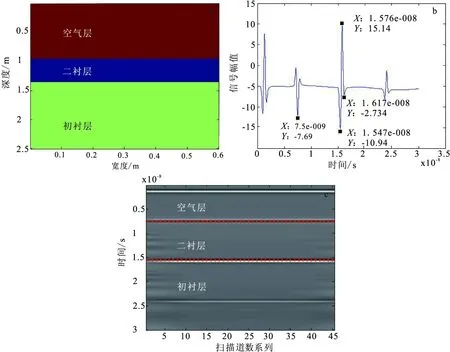
图2 正常隧道衬砌自动追踪结果Fig.2 Model of normal tunnel lining(a)正常隧道模拟图像；(b)正常隧道处理后信号；(c)正常隧道自动识别追踪结果

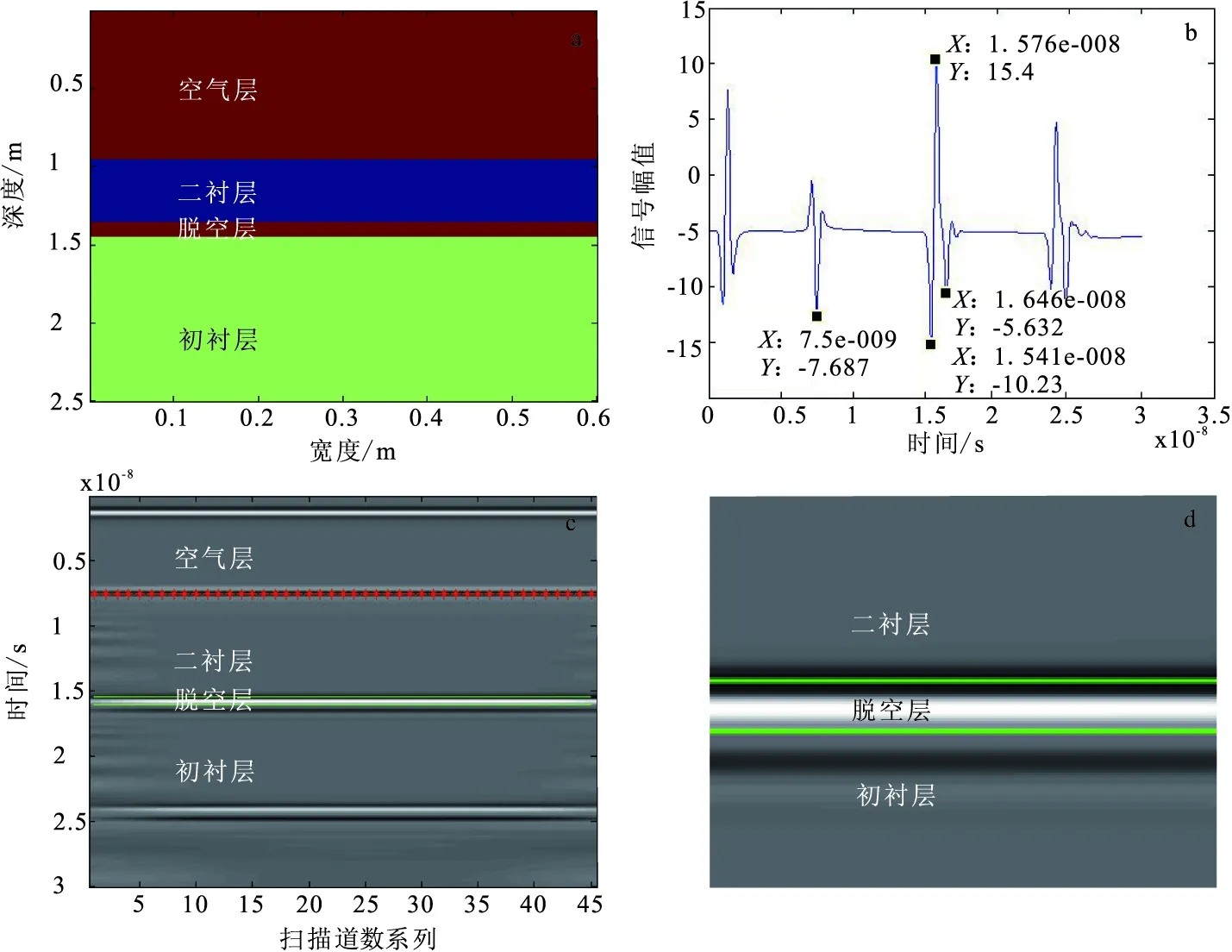
图3 脱空隧道衬砌自动追踪结果Fig.3 Model of tunnel lining with void(a)脱空隧道模拟图像；(b)脱空隧道处理后信号；(c)脱空隧道自动识别追踪效果；(d)脱空层局部放大图

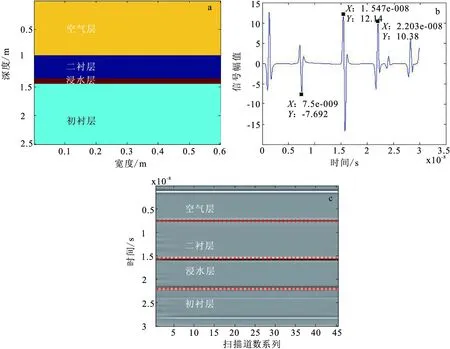
图4 浸水隧道衬砌自动追踪结果Fig.4 Model of tunnel lining with cavity water(a)浸水隧道模拟图像；(b)浸水隧道处理后信号；(c)浸水隧道自动识别追踪效果

在图2正常隧道衬砌模型中，第一层介质为空气，厚度为90 cm；第二层介质为二衬，厚度为S二T=40 cm，介质的相对介电常数为9，电导率为0.03；第三层介质为初衬，厚度为115 cm，介质的相对介电常数为4，电导率为0.02。

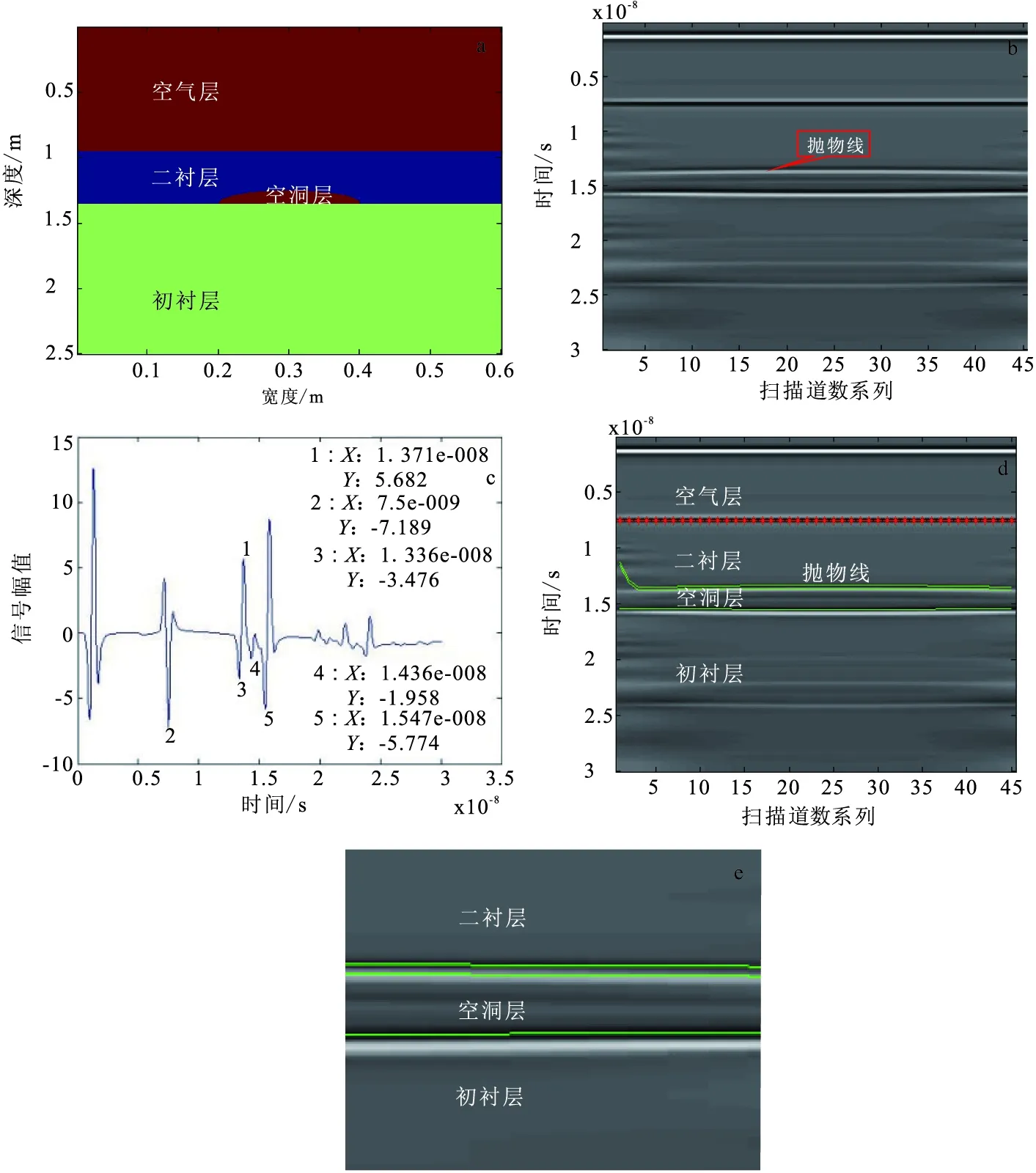
图5 含空洞隧道衬砌自动追踪结果Fig.5 Model of tunel lining with cavity(a)含空洞隧道模拟图像；(b)含空洞隧道雷达剖面图；(c)含空洞隧道处理后信号；(d)含空洞隧道自动识别追踪效果；(e)空洞层局部放大图

雷达波在二次衬砌层两个界面的反射时间分别为t11=7.5 ns，t12=15.7 ns，t13=t12-t11=15.47 ns-7.5 ns=7.97 ns。

通过以上分析，根据反射波波峰或波谷与反射界面一一对应的特征，编写程序，得到了两条平行直线，分别是空气与二衬、二衬与围岩的分界层。

在图3脱空隧道衬砌中，第一层介质为空气层，厚度为90 cm；第二层介质为二衬，厚度S二T=40 cm，介质的相对介电常数为9，电导率为0.03；第三层介质为脱空层，厚度ST=10 cm，介质的相对介电常数为“1”，电导率为“0”；第四层介质为初衬，厚度为105 cm，介质的相对介电常数为4，电导率为0.02。

在有脱空的隧道衬砌中，雷达波在二次衬砌层两个界面的反射时间分别为t21=7.5 ns，t22=15.41 ns，t23=t22-t21=15.41 ns-7.5 ns=7.91 ns，在脱空层两个界面的反射时间分别为tT1=15.41 ns，tT2=15.76 ns，tT3=tT2-tT1=15.76 ns-15.41 ns=0.35 ns。根据脱空下界面反射波的震荡波的第二个峰值与上界面的震荡波第三个波峰值的时间差tT4=16.46 ns-16.17 ns=0.29 ns，可推断出下界面反射时间为tT3+tT4=0.35 ns+0.29 ns=0.64 ns。

通过以上分析，根据反射波波峰或波谷与反射界面一一对应的特征，编写程序，得到了三条平行直线，第一条直线是空气和二衬的分界层；下面两条平行直线，分别是二衬和脱空、脱空和初衬的分界层。

在图4浸水隧道衬砌中，第一层介质为空气，厚度为90 cm；第二层介质为二衬，厚度S二S=40 cm，介质的相对介电常数为9，电导率为0.03；第三层介质为浸水层，厚度SS=10 cm，介质的相对介电常数为81，电导率为0.01；第四层介质为初衬，厚度为105 cm，介质的相对介电常数为4，电导率为0.02。

在有浸水的隧道衬砌中，雷达波在二次衬砌两个界面的反射时间分别为t31=7.5 ns，t32=15.47 ns，t33=t32-t31=15.47 ns-7.5 ns=7.97 ns。在浸水两个界面的反射时间分别为ts1=15.47 ns，tS2=22.03 ns，ts3=ts2-ts1=22.03 ns-15.47 ns=6.56 ns。

通过以上分析，根据反射波波峰或波谷与反射界面一一对应的特征，编写程序，得到了三条平行直线，分别为空气与二衬、二衬与水、水与围岩的分界层。

在图5含空洞的隧道衬砌中，第一层介质为空气，厚度为90 cm；第二层介质为二衬，厚度S2D=40 cm，介质的相对介电常数为9，电导率为0.03；第三层介质为初衬，厚度为115 cm，介质的相对介电常数为4，电导率为0.02；病害介质为空洞，空洞半径RD=10 cm，介质的相对介电常数为“1”，电导率为“0”。

在含空洞的隧道衬砌中，雷达波在二衬两个界面的反射时间分别为tD1=7.5 ns，tD2=13.36 ns，tD3=tD2-tD1=13.36 ns-7.5 ns=5.86 ns。

通过以上分析，根据反射波波峰或波谷与反射界面一一对应的特征，编写程序，得到了三条线，第一直线是空气和二衬的分界层；和病害介质同为空气的脱空隧道衬砌相比，第二条线为抛物线，是二衬与空洞的分界层；第三层直线是空洞与围岩的分界层。

在图6错位隧道砌中，第一层介质为空气，厚度为90 cm；第二层介质为二衬，错位之前二衬厚度S2c1=40 cm，错位之后二衬厚度S2c2=30 cm，介质的相对介电常数为9，电导率为0.03；第三层介质为初衬，错位之前初衬厚度为115 cm，错位之后初衬厚度为125 cm，介质的相对介电常数为4，电导率为0.02。

在有错位的隧道衬砌中，两个单道波分别为错位前、后一扫描道上的波形，雷达波在错位前二衬两个界面的反射时间分别为tC11=7.5 ns，tC12=15.41 ns，tC13=tC12-tC11=15.41 ns-7.5 ns=7.91 ns。雷达波在错位后二衬两个界面的反射时间分别为tC21=7.5 ns，tC22=13.36 ns，tC23=tC22-tC21=13.36 ns-7.5 ns=5.86 ns。

通过以上分析，根据反射波波峰或波谷与反射界面一一对应的特征，编写程序，得到了三条直线，第一条完整的直线是空气和二衬的分界层；剩下两个半条平行直线，为错位衬砌和围岩的分界层。

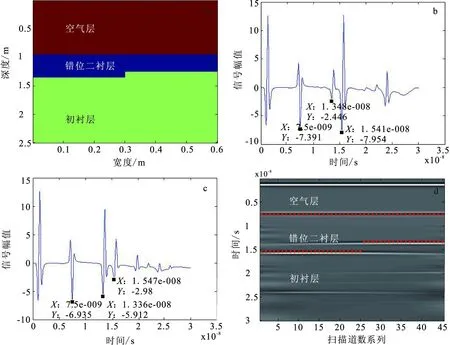
图6 错位隧道衬砌自动追踪结果Fig.6 Model of tunnel lining with dislocation(a)错位衬砌模拟图像；(b)错位前隧道处理后信号；(c)错位后隧道处理信号；(d)错位隧道自动识别追踪效果

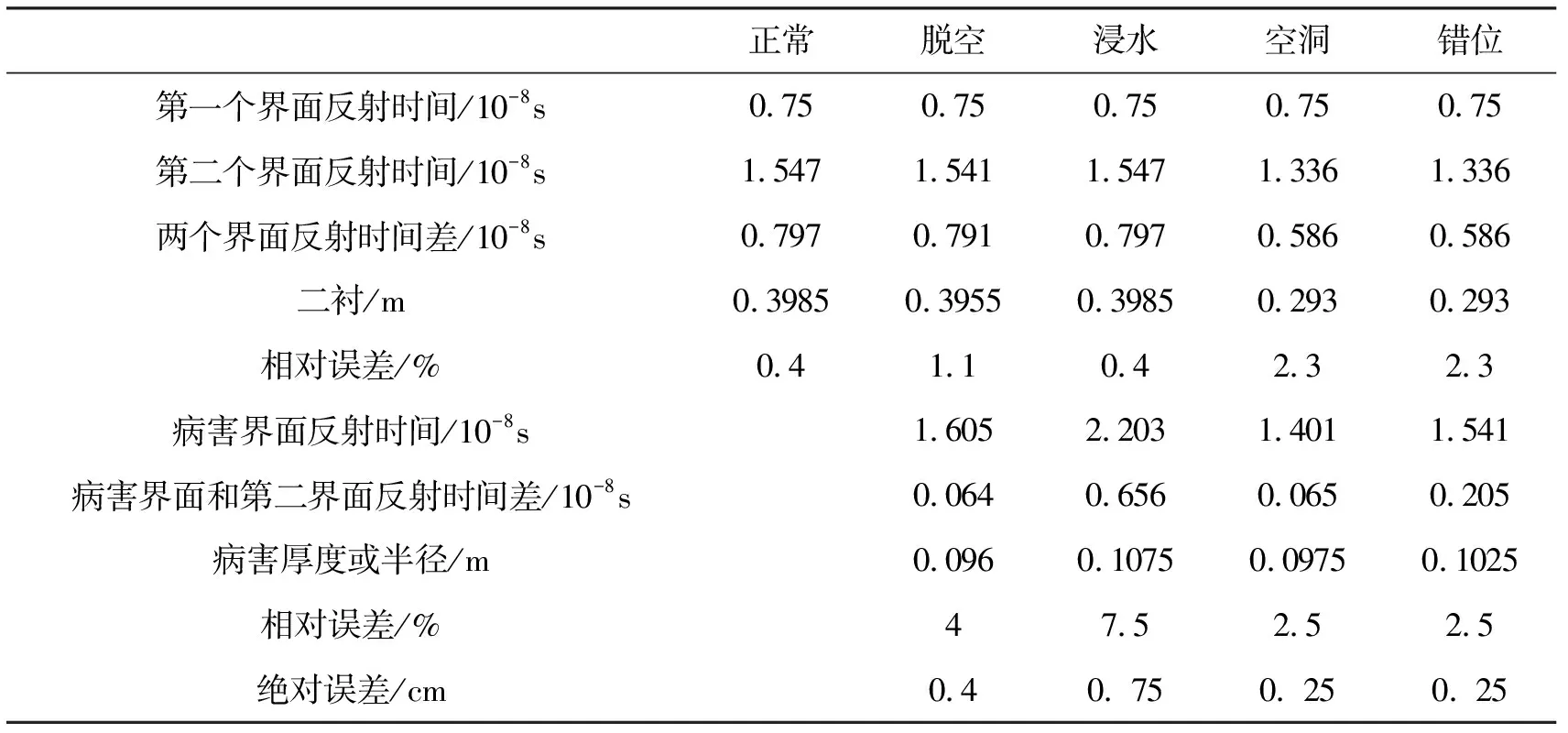
正常脱空浸水空洞错位第一个界面反射时间/10-8s0.750.750.750.750.75第二个界面反射时间/10-8s1.5471.5411.5471.3361.336两个界面反射时间差/10-8s 0.7970.7910.7970.5860.586二衬/m0.39850.39550.39850.2930.293相对误差/%0.41.10.42.32.3病害界面反射时间/10-8s1.6052.2031.4011.541病害界面和第二界面反射时间差/10-8s0.0640.6560.0650.205病害厚度或半径/m0.0960.10750.09750.1025相对误差/%47.52.52.5绝对误差/cm0.40. 750. 250. 25

从以上反射时间可以看出，根据隧道衬砌的分层特征，在隧道衬砌中，可以自动识别衬砌分界层，通过计算隧道衬砌的厚度，用来检测隧道是否发生病害，当判断出隧道衬砌发生了病害时，也可以根据不同病害的不同特征，识别出隧道衬砌病害的厚度。

3 结论

笔者对铁路隧道衬砌层位自动识别追踪进行模拟研究，对模拟得到的探地雷达数据进行数据处理，并分析总结隧道衬砌层位特征，根据反射波的波谷或波峰出现的时间和相应深度的衬砌层面一一对应的波形特征，利用Matlab编程来自动识别衬砌分界层，从而用来检测隧道衬砌厚度，并且当隧道衬砌含有病害时，根据特征，不仅可以识别隧道衬砌厚度，也能可以识别出隧道衬砌病害的厚度。通过以上计算分析，可知当所有工况都存在于同一隧道横截面时，自动识别追踪的方法是：①按照正常隧道衬砌模型特征进行追踪，追踪结果如果没有出现错位现象，并且在其上方存在抛物线状反射波，则说明为空洞隧道衬砌，否则为正常隧道衬砌；②如果出现错位现象，但在其下方较远处存在直线状较强反射波，则说明为浸水隧道衬砌，若在其下方较近处存在直线状较强反射波，则说明为脱空隧道衬砌，否则为错位隧道衬砌；③可以根据具体反射波的时间来具体判断衬砌或者病害的厚度。