基于MCMC方法的WOFOST模型参数标定与不确定性分析

黄健熙，黄 海，马鸿元，李 颖，侯英雨，何 亮，朱德海

(1. 中国农业大学土地科学与技术学院，北京 100083；2. 农业部农业灾害遥感重点实验室，北京 100083；3. 中国气象局河南省农业气象保障与应用技术重点开放实验室，郑州 450003；4. 河南省气象科学研究所，郑州 450003；5. 中国气象局国家气象中心，北京 100081)

0 引 言

气候变化、人口膨胀、资源短缺等一系列问题对农业的高效持续发展提出了更高要求，如何在宏观上准确地进行作物估产，获取作物生长关键性参数，以帮助确保粮食安全，已经越来越成为研究的热点。基于机理过程模拟的作物生长模型普遍用于农作物产量预报、参数估计、灾害影响评估[1-7]，还有学者将其成功应用于作物重金属、营养品质监测等[8-9]，在不同区域环境、不同作物研究中均得到广泛验证。

作物模型机理性模拟的准确性依赖于众多模型参数、气象驱动数据、土壤参数的准确获取，模型应用的区域越大，数据的直接、准确获取越困难，模拟的精度也越难以保证。实际应用中，往往将一定的地理区域进行人为的均质化，在此区域内共用全部或者部分模型参数，由此不可避免的引起代表性误差。为了更准确反映出区域模型模拟的空间变异性，降低以点代面导致的误差，近年来众多学者将遥感观测数据对作物模型进行约束，通过数据同化在空间上对模型参数进行优化，取得了大量的成果[3-5,10-12]。然而，诸多研究中鲜有对模型参数标定的详尽描述，也缺乏模型不确定性的定量表达，使得模型在更大区域上的应用可靠性受到质疑。

所谓模型参数标定，就是调整模型参数使其适用于特定的研究区域。传统方法是采用一定数量的实测值，通过试错法标定出一套“最适”参数，这种标定方法很难准确代表空间变异性的结果的综合。并且由于数据代表性、测量精度、标定方法等限制，常常基于一组观测值会得到多组相异参数，即模型的“异参同效”现象。因此，无论是“以点代面”的区域模拟，还是更大范围的模型同化应用，都迫切需要更为科学精确的参数标定方法以及标定后参数不确定性的定量评价方法。

基于贝叶斯理论的 MCMC（Markov chain Monte Carlo，马尔科夫链-蒙特卡洛）方法能够结合观测数据和参数的先验知识得到模型参数的后验分布，从而利用参数后验样本的均值或中值作为参数标定结果，并且可以通过后验样本的均方根偏差定量的表达模型参数的不确定性。MCMC方法在水文模型[13-15]、森林管理模型[16]、林冠蒸腾模型[17]等模型参数标定研究中已得到较多应用，并且显示出较强的适用性，其在作物模型参数标定与不确定性评价中也逐渐得到应用[18-20]。中国的作物模型应用面临地形复杂、气候多样空间异质性挑战，因此模型参数也具有更大的不确定性。利用MCMC方法对中国小麦种植区作物模型参数较大范围的标定、不确定性评价以及比较目前还少有报道，因此需要进一步研究探索。

本研究实现利用融入 snooker更新算法的 DE-MC（differential evolution Markov chain ，差分进化马尔科夫链）方法在Python环境下对WOFOST作物生长模型参数进行标定和不确定性分析。标准的 DE-MC算法由Braak等[21]于2006年提出，并通过引入snooker更新算法进一步改进，研究表明融入snooker更新的DE-MC算法能够通过少至3条的并行链实现对多达50～100维参数空间的后验估计[22]。在河南郑州农业气象站点上，结合多年实测LAI（leaf area index，叶面积指数）和产量数据得到参数后验分布，实现对模型参数的估计和不确定性评价。

1 数据及模型

1.1 研究数据

本文所用的试验观测数据来自河南郑州农业气象试验站2008—2012年的观测数据，其中2008—2011年数据用于模型参数标定，2012年数据用于标定结果验证。研究区均位于种植区划中的黄淮冬麦区，耕作模式主要为一年两熟，小麦生育期降水约 120～140 mm，播种期至成熟期大于0 ℃积温2 100～2 300 ℃，无霜期180～200 d。冬小麦播种期一般为10月份上中旬，成熟期一般为次年5月下旬到6月上旬。

作物数据主要包括从播种到成熟各个生育期的时间、生长状况、管理措施、土壤情况、产量及产量结构等。其中，LAI观测值分别对应三叶期、分蘖期、越冬始期、返青期、拔节期、抽穗期和乳熟期 7个生育时期；模型运行所需气象数据来自中国科学院青藏高原研究所制作中国区域地面气象要素数据集[23]，该数据是用于驱动陆面模型模拟的栅格数据集，包括近地面气温、近地面气压、近地面空气比湿、近地面全风速、地面向下短波辐射、地面向下长波辐射与降水率共7个要素。

1.2 WOFOST模型

WOFOST模型是荷兰瓦赫宁根大学开发的一个机理性过程模型，基于光截获和二氧化碳同化作为驱动过程来描述作物生长，并将物候发育作为生长控制过程，分别用 0、1、2代表作物出苗、开花、成熟 3个生育期（development stage，DVS）。

本研究采用 Python下的 PCSE 5.3.1（python crop simulation environment，PCSE）软件包进行WOFOST的运行。PCSE提供了作物模型模拟的环境、读取数据（如气象、土壤、农艺管理等）的工具、模拟生物物理过程（如物候、呼吸、蒸散发等）的模块。相比于传统FORTRAN版本的作物模型，PCSE是用纯Python代码编写，使其具有更加灵活、易于修改和拓展的特性，并可轻松连接数据库、图形用户界面、可视化工具和数值统计软件包。有关PCSE更详细的介绍可以参考网站：https://pcse.readthedocs.org或者http://github.com/ajwdewit/pcse。

1.3 标定参数选择

本研究利用LAI和产量观测值对模型参数进行标定，与积温有关的作物参数直接依据作物物候发育日期与近地面气温计算得到。其余作物参数通过 Sobol方法[24-25]进行全局敏感性分析，以Sobol全局敏感性指数大于0.05作为参数敏感的标准，选取对不同生育期LAI以及成熟期产量敏感的参数作为待标定参数。

2 研究方法

2.1 MCMC方法

贝叶斯理论能够结合模型参数的先验知识和模型输出对应的观测值，实现对模型参数的后验估计。MCMC方法即在贝叶斯理论框架下，构造以参数后验分布为平稳分布的马尔科夫链，从而得到参数的后验样本，基于这些样本实现对参数数字特征的推断。贝叶斯理论用公式表达如下

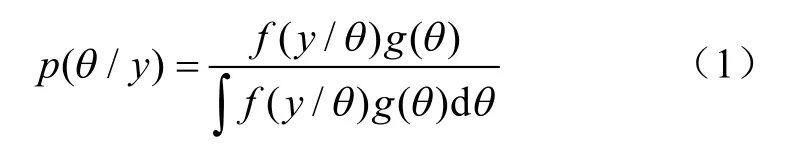
式中θ和y分别代表WOFOST模型的参数和模拟输出值（如LAI、产量等）；p(θ/y)为参数的后验概率密度函数；f(y/θ)为观测值似然函数；g(θ)为参数的先验分布。研究中，将模型的驱动数据，如气象数据、降水等，记为x，则式（1）可以改为

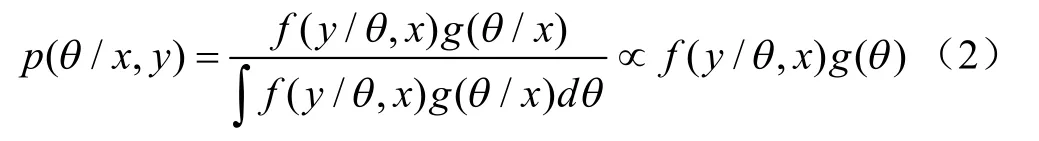
引入MCMC方法的目的就是通过结合实测数据得到模型参数后验样本和并定量评价其不确定性，研究中，模型参数的不确定性用MCMC方法标定得到的参数后验样本的均方根偏差RMSDq计算

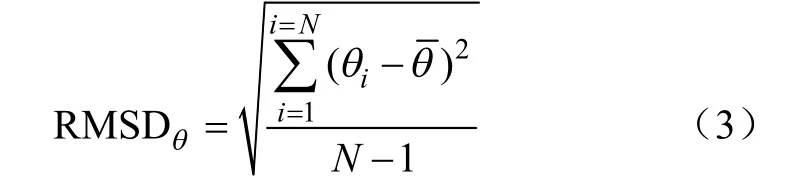
式中N表示参数θ后验样本个数；θi表示第i个后验参数；表示参数θ后验样本均值，当θ服从高斯分布时，RMSDθ可以作为θ总体标准差的无偏估计。

为便于比较不同参数样本内部的离散程度，对每个参数后验分别再计算相对均方根偏差RRMSDq，定义为

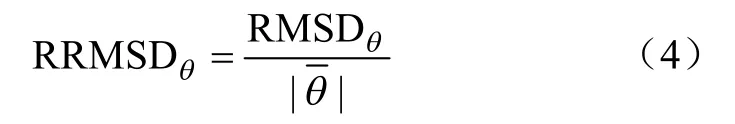
式中RMSDθ表示参数θ的均方根偏差，`表示参数θ后验样本均值。

2.2 DE-MC算法及snooker更新

差分进化马尔科夫链(differential evolution Markov chain, DE-MC)算法[21]通过多条平行链的运行，以实现更好的探索参数空间。但标准DE-MC算法中并行链数必须大于参数空间的维数。为了提高采样效率，Braak等[22]在提出DE-MC算法的基础上，引入snooker更新算法[26-27]以部分取代其中的平行方向更新（parallel direction update），克服了标准DE-MC中并行链数必须大于维数的限制，发展成为DE-MC(Z)S算法。本文基于这种思想实现算法的构建，主要步骤为：

1）初始化M0´d维的矩阵Z，即依据先验分布随机生成M0组参数，其中M0>max(d,N),然后复制矩阵Z中前N行，记为种群（population）X，并设置M←M0；

2）设置一定的次数K，每逢K倍对X进行更新（update）。

3）将更新后的X添加到Z中，即M←M+N；

4）如果X已经达到收敛（本研究通过比方差法（variance ratio）[28]进行判断），或者总的更新次数超过了程序设定值，则进行到第5步，否则回到步骤2；

5）丢弃Z中一部分较早状态的样本（burn in），并进行一定比例的细化（thin），最终得到参数的后验样本。

其中每次对X的更新形成一个世代周期（generation cycle），并依次对链x1,x2,…,xN进行更新，首先随机生成0到1之间的随机数，如果小于0.1，则进行snooker更新，否则按照标准的 DE-MC算法进行平行方向更新[22]。snooker更新的步骤为：

1）选择另外一条处于状态z的链；

2）沿着xiz方向按如下步骤依概率密度采样，

① 选择另外2条分别处于状态zR1和zR2的随机链R1和R2，

② 将zR1和zR2正射投影到xiz方向，并分别生成zP1和zP2，

③ 提议x*←xi+γs(zP1-zP1)，其中γs为缩放因子，取1.2～2.2之间的随机数，

④计算Metropolis系数：

⑤ 以概率min(1,r)接受提议，否则保持xi状态不变。

3 结果与分析

3.1 Sobol敏感性分析结果

Sobol全局敏感性分析结果表明，对三叶期LAI敏感的参数包括SLATB00（specific leaf area at development stage of 0，生育期为0时的比叶面积）、TBASEM（lower threshold temperature for emergence，出苗的低温阈值）、TDWI（initial total crop dry weight，作物初始干物质质量）、SLATB020（specific leaf area at development stage of 0.2，生育期为0.2时的比叶面积）；对分蘖期LAI敏感的参数包括SLATB00、SLATB020、TBASEM、AMAXTB00（maximum CO2assimilation rate at development stage of 0，生育期为 0时的单叶最大二氧化碳同化速率）；对越冬期 LAI敏感的参数包括 SLATB00、SLATB020、TBASEM、AMAXTB00、TBASE（lower threshold temperature for aging of leaves，叶龄的低温阈值）、TMNFTB_min（low temperature threshold when reduction factor of gross assimilation rate is 0，总同化率降低因子为0时的低温阈值）；对返青期 LAI敏感的参数包括SLATB00、SLATB020、TMNFTB_min、TBASEM、TBASE、AMAXTB00；对拔节期 LAI敏感的参数包括SLATB040（specific leaf area at development stage of 0.4，生育期为 0.4时的比叶面积）、SLATB00、TBASE、SLATB020、AMAXTB00、 SLATB070（specific leaf area at development stage of 0.7，生育期为0.7时的比叶面积）、TMNFTB_min、RGRLAI（maximum relative increase in LAI，叶面积指数最大增长率）；对抽穗期LAI敏感的参数包括 SLATB070、SLATB040、SLATB00、TBASE、KDIFTB100（extinction coefficient for diffuse visible light at development stage of 1，生育期为1时的散射消光系数）、AMAXTB00、SLATB020、AMAXTB100（maximum CO2assimilation rate at development stage of 1，生育期为1时的单叶最大二氧化碳同化速率）；对乳熟期LAI敏感的参数包括SPAN（life span of leaves growing at 35 Celsius，在35 ℃时叶面积的生命周期）、SLATB070、KDIFTB100；对成熟期产量敏感的参数 SPAN、CVO（efficiency of conversion into storage organs，储存器官的同化物转换效率）、AMAXTB130（maximum CO2assimilation rate at development stage of 1.3，生育期为1.3时的单叶最大二氧化碳同化速率）、SLATB070、AMAXTB100、KDIFTB100、SLATB040。

上述敏感性分析是以2008年郑州农业气象试验站上数据运行分析得到的，由于TBASEM的改变会引起生育期在时间上的“漂移”，因而设置该参数为默认值，不进行标定。最终综合敏感性分析结果，选取 SLATB00、SLATB020、AMAXTB00、SLATB070、TBASE、AMAXTB100、KDIFTB100、SLATB040、TMNFTB_min、SPAN、CVO、AMAXTB130、RGRLAI、TDWI共计 14个参数作为待标定参数。

3.2 MCMC标定

3.2.1 参数先验分布

对14个参数设置为以模型默认值为初始值、在参数范围内的均匀分布。参数初始值及范围如表1。

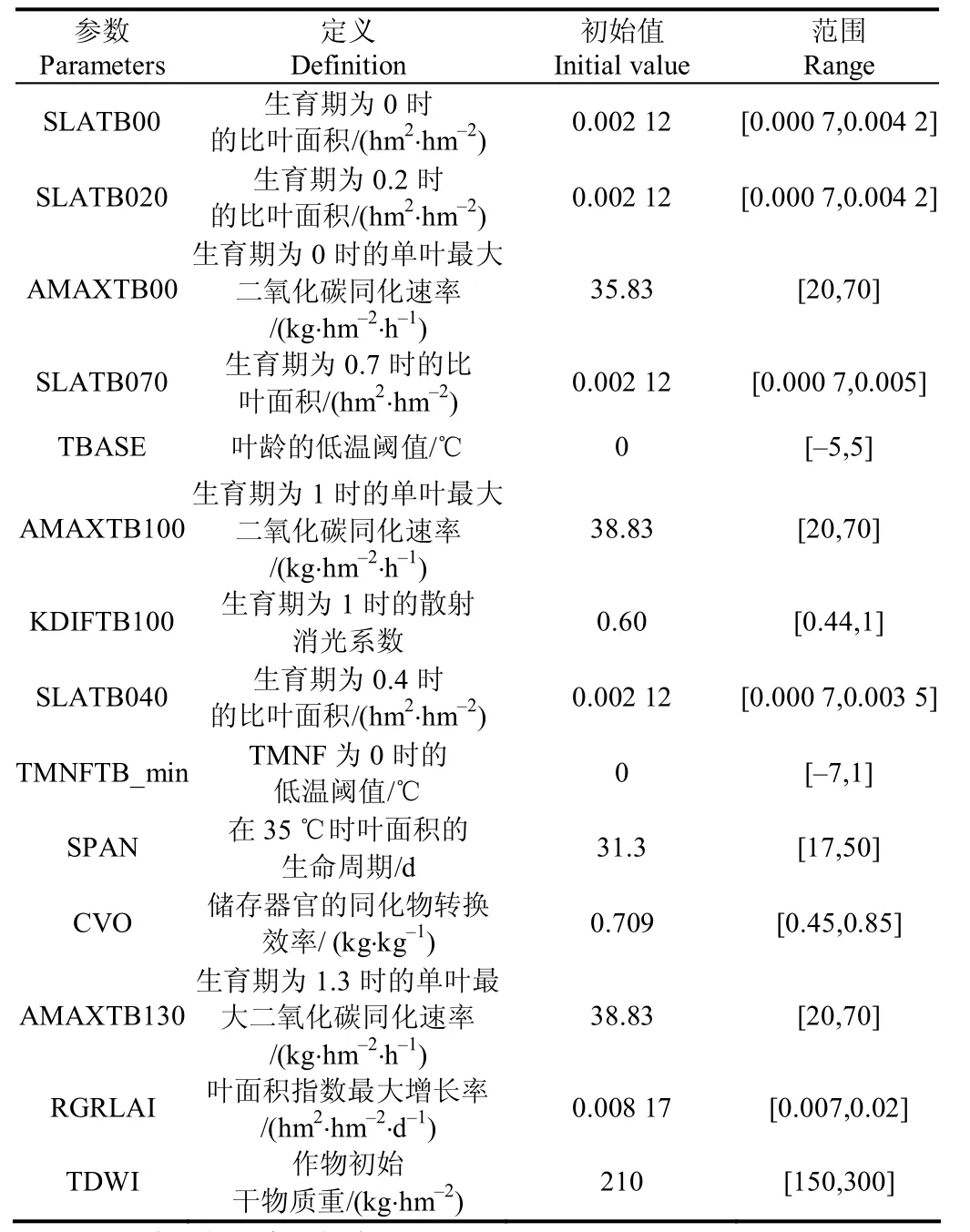
表1 待优化的14个参数的初始值及范围Table 1 Initial value and range of 14 parameters for optimization

3.2.2 似然函数的确定

本研究中认为LAI和产量服从以观测值为期望的高斯分布，由于概率密度可能非常小，为了避免位数舍入引起的误差，所有概率密度的计算均通过取对数形式计算，由此确立似然函数

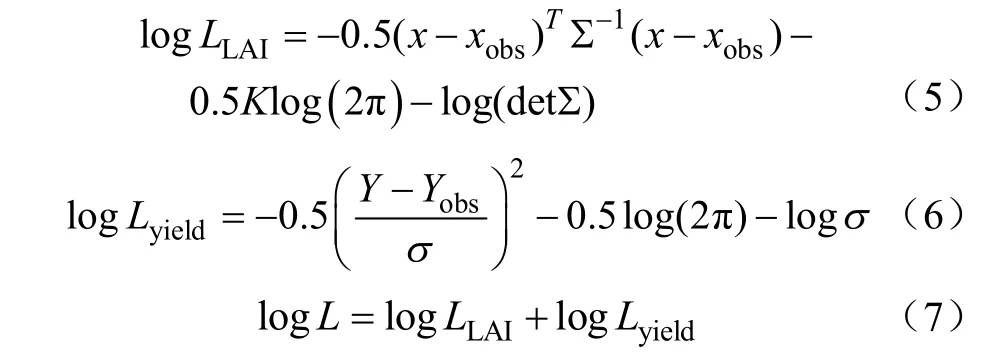
式中LLAI和Lyield分别表示LAI和产量的似然函数；L表示似然函数（likelihood function）的返回值；矢量x和xobs分别表示对应不同生育期LAI的模型模拟值和观测值；Σ表示LAI观测值的协方差矩阵，本研究中不同生育期LAI观测值相互独立，且方差均取0.2；K表示空间维数，即LAI观测值的个数；detΣ表示 Σ的行列式值；Y和Yobs分别表示成熟期产量的模型模拟值和观测值；σ表示产量观测值的标准差，本研究中取观测值的10%。

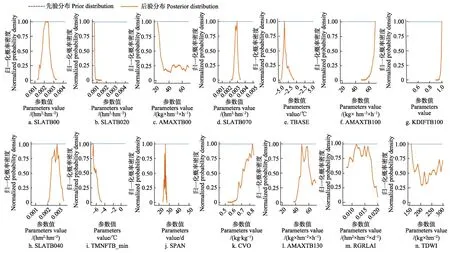
图1 14个参数的先验及后验分布Fig.1 Prior and posterior distribution of 14 parameters

3.2.3 参数的后验分布

本研究中设定DE-MC种群（并行链）数目为3，每5次采样进行一次种群进化（链的更新），每5 000次迭代通过比方差法进行一次收敛性判断，计算诊断指标ˆR[28]，ˆR>1时，表明链没有达到收敛，若ˆR≈1，表明链已经处于静止状态。本研究中当连续超过3次诊断指标ˆR<1.05，则认为马尔科夫链达到收敛。收敛后舍弃前2000次采样（burn-in），为解决自相关问题，并每隔5次对链进行细化，最终得到参数的后验样本及其分布。图1为14个参数先验及后验样本的分布图。表2列出了最终得到参数后验样本的均值、中值、95%置信区间、RMSD以及 RRMSD，结果均保留小数点后4位。

从图 1可以看出，相对于各参数的先验分布，参数的后验分布均出现较大改变，表明标定参数选取的有效性。由于WOFOST模型无法准确模拟越冬期小麦实际生长情况，因而在标定参数包含越冬期前后LAI观测值的情况下，部分参数的后验分布表现出极端变化，表现为：SLATB020集中分布在参数区间的左边界，这是因为模型运行时，比叶面积与LAI模拟值成正比例关系，生育期为0.2较为接近越冬期，由于WOFOST无法模拟低温导致的叶片损伤减少，其LAI“模拟期望值”很大程度上高于实际LAI值，因而在实际LAI观测值的标定下，导致该时期比叶面积极端减小以使模型模拟出较小的LAI值。同理，生育期为 1时大致处于抽穗期附近，此阶段 LAI值基本处于整个生育期的峰值，因而在抽穗期LAI峰值的影响下，AMAXTB100和KDIFTB100集中分布在参数区间的右边界。

除个别极端分布的参数，表 2中参数的后验样本均值和中值基本相一致。后验参数的 95%置信区间一定程度上反映了参数的合理取值区间，与表 1中参数的初始范围相比，其范围缩小的越多，也一定程度表明该参数标定后的不确定越小。RMSD和RRMSD描述了参数样本内部相对于均值的离散程度，可作为参数不确定性的定量评价。在参数符合高斯分布时，参数样本的 RMSD是参数总体高斯分布的标准差σ的无偏估计。由图1分布，可近似认为 SLATB00、SLATB070、SLATB040、SPAN、AMAXTB130符合高斯分布，以RRMSD为指标，不确定性由小到大依次为 SPAN、SLATB070、SLATB040、AMAXTB130、SLATB00。

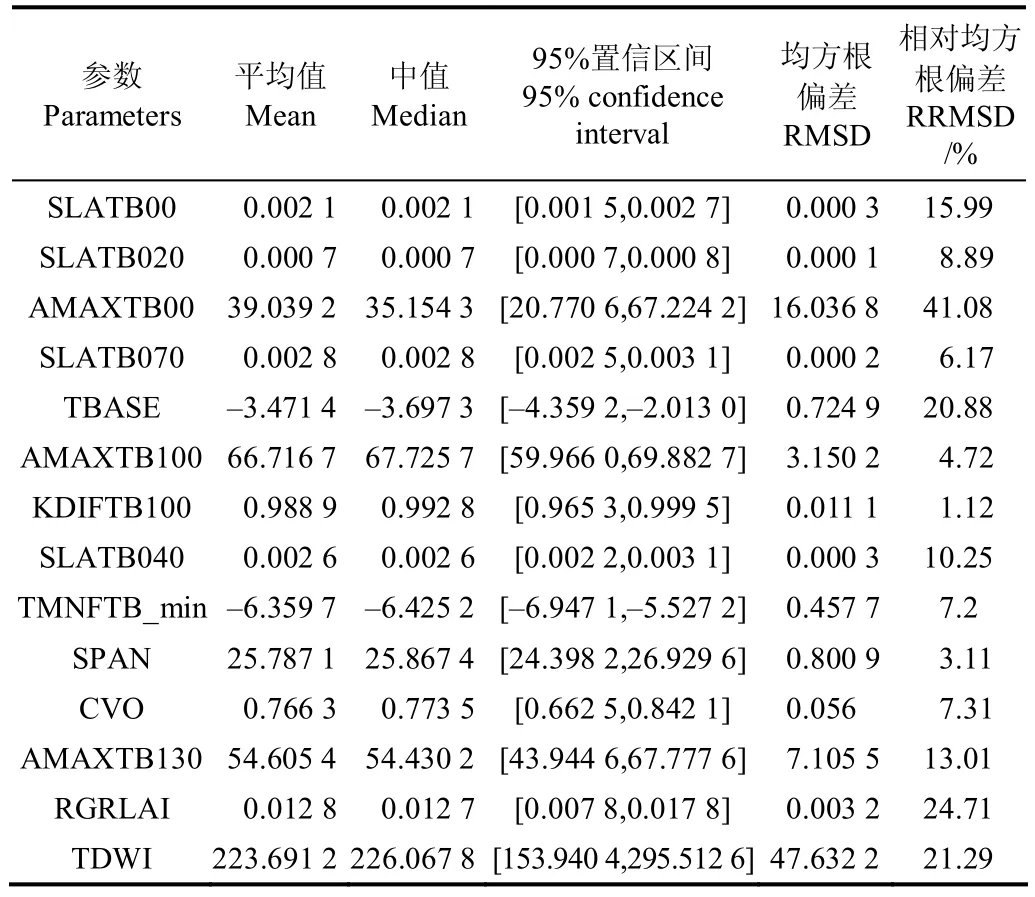
表2 参数后验样本的均值、中值、95%置信区间、RMSD、RRMSDTable 2 Mean, median, 95% confidence interval, RMSD and RRMSD of parameters posterior sample

3.3 标定运行结果

3.3.1 标定精度验证

以2012年生长季站点上气象数据为驱动，分别以参数初始值、后验均值和中值带入模型运行，与观测值进行比较，结果如图2所示。计算LAI模拟值和对应观测值间的均方根误差（RMSE）作为精度评价指标，公式为

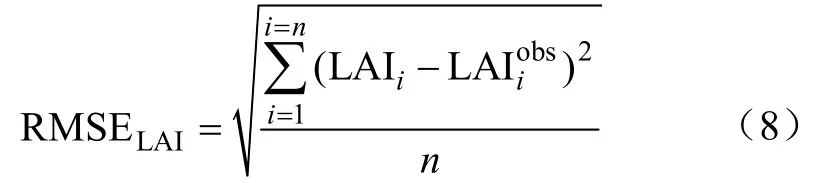
式中LAIi表示第i个LAI模拟值，LAIiobs表示第i个对应的观测值，n表示LAI观测值个数。结果显示：参数初始值（模型默认参数）、后验均值和后验中值带入模型模拟的LAI值的RMSE分别为1.79、0.84、0.87，相比于初始值，标定后LAI模拟精度分别提高了53.07%（后验均值）和51.40%（后验中值）；产量模拟精度从初始值的75.15%提高至 83.40%（后验均值）和 84.03%（后验中值），模拟精度提高8.25%~8.88%。这表明利用MCMC标定得到的后验样本均值和中值在很大程度能够实现对观测数据的拟合。此外，由图 2可以发现，相比于初始状态，标定后并非在每个观测节点上都提高了精度，但是却在整体上提高了与观测数据的拟合精度。标定后的LAI曲线较好的捕捉到了LAI的峰值，但是在越冬期前后的LAI模拟值具有较大误差，主要是由于WOFOST模型开发之初主要是为了模拟欧洲的作物生长，并未实现中国冬小麦越冬期情况模拟[29]。

标定后的产量模拟精度较初试状态有所提高，但相对观测值仍有一定误差，这很大程度上是因为用于标定的2008—2011年的产量数据仅仅是4个标量值，并不能够充分实现对产量形成相关参数的准确标定，进一步研究可以引入生育期内的穗重数据进行标定，以提高产量标定精度。

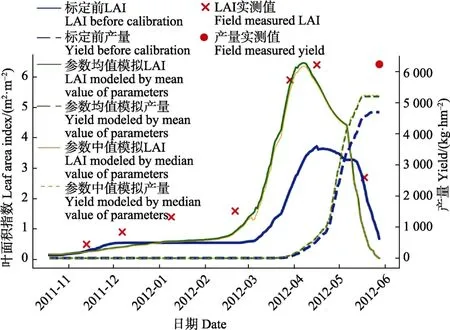
图2 参数标定前后模型模拟结果对比Fig.2 Comparison of model simulated results before and after parameters calibration

3.3.2 模型输出的不确定性评价

将后验样本作为参数集合，分别带入WOFOST模型并输出得到LAI和产量时间序列上的模拟集合，结果如图 3所示。由阴影部分的走势可以直观的反映出后验参数集模拟结果所代表的不确定性，整体上LAI模拟的不确定性在三叶期至返青期之间以及LAI曲线峰值（拔节期至抽穗期之间）较大，其它时期相对稳定。产量模拟的不确定性在开始模型模拟籽粒形成开始逐渐扩大，并在乳熟期达到最大，至成熟期基本趋于稳定。

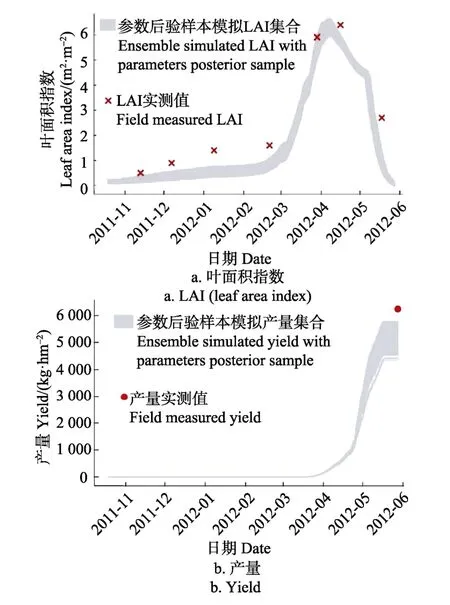
图3 参数标定后模型模拟LAI和产量的不确定性Fig.3 Uncertainty of model simulated LAI and yield with calibrated parameters dataset

4 结 论

本研究以郑州农业气象试验站2008—2011年观测数据作为标定数据，选取14个敏感参数，运用融入snooker更新的DE-MC方法实现参数的标定，并用2012年的观测数据进行了验证，得到结论如下：

1）以模型默认参数为初始值，通过DE-MC方法可以实现参数的自动标定，相比于模型默认参数模拟结果，参数标定后LAI模拟精度可提高51.40%~53.07%，产量模拟精度提高8.25%~8.88%。

2）以生育期内LAI观测值和成熟期产量为标定数据，SPAN、SLATB070、SLATB040、AMAXTB130 和 SLATB00的后验分布可近似为高斯分布，其中 SPAN的不确定性最低。

3）带入后验参数集合进行模型，LAI在三叶期至返青期之间以及拔节期至抽穗期之间模拟的不确定性较大；产量模拟的不确定性随时间不断增大，至乳熟期前后达到稳定。

本研究使用的标定数据为农业气象站点上的观测数据，虽然作物品种一致，但年际间的栽培管理措施并未严格进行控制（如播种密度等），导致标定结果的精度可能受到一定影响。后续可在更多地区，采用具有定量控制的试验数据开展研究，以进一步验证本方法的有效性。

[1]Wang H, Zhu Y, Li W, et al. Integrating remotely sensed leaf area index and leaf nitrogen accumulation with RiceGrow model based on particle swarm optimization algorithm for rice grain yield assessment[J]. Journal of Applied Remote Sensing, 2014, 8(1): 83674.

[2]Huang J, Tian L, Liang S, et al. Improving winter wheat yield estimation by assimilation of the leaf area index from Landsat TM and MODIS data into the WOFOST model[J].Agricultural & Forest Meteorology, 2015, 204: 106－121.

[3]He B, Li X, Quan X, et al. Estimating the aboveground dry biomass of grass by assimilation of retrieved LAI into a crop growth model[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2015, 8(2): 550－561.

[4]王东伟，王锦地，梁顺林. 作物生长模型同化 MODIS反射率方法提取作物叶面积指数[J]. 中国科学：地球科学，2010(1)：73－83.Wang Dongwei, Wang Jindi, Liang Shunlin. Assimilating MODIS reflectance into crop growth model to extract crop leaf area index [J]. Scientia Sinica Terrae, 2010(1): 73－83.(in Chinese with English abstract)

[5]Fang H, Liang S, Hoogenboom G, et al. Corn-yield estimation through assimilation of remotely sensed data into the CSM-CERES-Maize model[J]. International Journal of Remote Sensing, 2008, 29(10): 3011－3032.

[6]张建平，赵艳霞，王春乙，等. 基于 WOFOST作物生长模型的冬小麦干旱影响评估技术[J]. 生态学报，2013，33(6)：1762－1769.Zhang Jianping, Zhao Yanxia, Wang Chunyi, et al. Evaluation technology on drought disaster to yields of winter wheat based on WOFOST crop growth model[J]. Acta Ecologica Sinica, 2013, 33(6): 1762－1769. (in Chinese with English abstract)

[7]马玉平，王石立，李维京. 基于作物生长模型的东北玉米冷害监测预测[J]. 作物学报，2011，37(10)：1868－1878.Ma Yuping, Wang Shili, Li Weijing. Monitoring and predicting of maize chilling damage based on crop growth model in Northeast China[J]. Acta Agronomica Sinica, 2011,37(10): 1868－1878. (in Chinese with English abstract)

[8]Jin M, Liu X, Wu L, et al. An improved assimilation method with stress factors incorporated in the WOFOST model for the efficient assessment of heavy metal stress levels in rice[J].International Journal of Applied Earth Observations &Geoinformation, 2015, 41: 118－129.

[9]李振海. 基于遥感数据和气象预报数据的 DSSAT模型冬小麦产量和品质预报[D]. 杭州：浙江大学，2016.Li Zhenhai. Predicting Winter Wheat Yield and Quality by Integrating of Remote-sensing Data and the Weather Forecast Data Into the DSSAT Model[D]. Hangzhou: Zhejiang University, 2016. (in Chinese with English abstract)

[10]Huang J, Sedano F, Huang Y, et al. Assimilating a synthetic Kalman filter leaf area index series into the WOFOST model to improve regional winter wheat yield estimation[J].Agricultural & Forest Meteorology, 2016, 216: 188－202.

[11]Ma H, Huang J, Zhu D, et al. Estimating regional winter wheat yield by assimilation of time series of HJ-1 CCD NDVI into WOFOST–ACRM model with Ensemble Kalman Filter[J].Mathematical & Computer Modelling, 2013, 58(3-4):753－764.

[12]Morel J, Todoroff P, Bégué A, et al. Toward a satellite-based system of sugarcane yield estimation and forecasting in smallholder farming conditions: A case study on Reunion Island[J]. Remote Sensing, 2014, 6(7): 793708.

[13]Rwasoka D T, Madamombe C E, Gumindoga W, et al.Calibration, validation, parameter indentifiability and uncertainty analysis of a 2 – parameter parsimonious monthly rainfall-runoff model in two catchments in Zimbabwe[J].Physics & Chemistry of the Earth Parts A/b/c, 2014,67–69(12): 36－46.

[14]Hassan A E, Bekhit H M, Chapman J B. Using Markov Chain Monte Carlo to Quantify Parameter Uncertainty and Its Effect on Predictions of a Groundwater Flow Model.[M].Elsevier Science Publishers B. V., 2009.

[15]Gallagher M, Doherty J. Parameter estimation and uncertainty analysis for a watershed model[J]. Environmental Modelling & Software, 2007, 22(7): 1000－1020.

[16]Van O M, Reyer C, Bohn F J, et al. Bayesian calibration,comparison and averaging of six forest models, using data from Scots pine stands across Europe[J]. Forest Ecology &Management, 2013, 289(2): 255－268.

[17]Li X, Yang P, Ren S, et al. An improved canopy transpiration model and parameter uncertainty analysis by Bayesian approach[J]. Mathematical & Computer Modelling An International Journal, 2010, 51(11, 12): 1368－1374.

[18]Toshichika I, Masayuki Y, Motoki N. Parameter estimation and uncertainty analysis of a large-scale crop model for paddy rice: Application of a Bayesian approach[J].Agricultural & Forest Meteorology, 2009, 149(2): 333－348.

[19]Marin F, Jones J W, Boote K J. A stochastic method for crop models: including uncertainty in a sugarcane model[J].Agronomy Journal, 2017, 109(2).

[20]何亮，侯英雨，赵刚，等. 基于全局敏感性分析和贝叶斯方法的 WOFOST作物模型参数优化[J]. 农业工程学报，2016，32(2)：169－179.He Liang, Hou Yingyu, Zhao Gang, et al. Parameters optimization of WOFOST model by integration of global sensitivity analysis and Bayesian calibration method[J].Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(2): 169－179. (in Chinese with English abstract)

[21]Braak C J F T. A Markov chain Monte Carlo version of the genetic algorithm differential evolution: Easy Bayesian computing for real parameter spaces[J]. Statistics &Computing, 2006, 16(3): 239－249.

[22]Braak C J T, Vrugt J A. Differential evolution Markov chain with snooker updater and fewer chains[J]. Statistics &Computing, 2008, 18(4): 435－446.

[23]何杰，阳坤. 中国区域高时空分辨率地面气象要素驱动数据集[Z]. 寒区旱区科学数据中心，2011.

[24]Sobol, I. M. Global Sensitivity Indices for Nonlinear Mathematical Models and Their Monte Carlo Estimates[M].Elsevier Science Publishers B. V., 2001.

[25]Zhang X Y, Trame M N, Lesko L J, et al. Sobol sensitivity analysis: A tool to guide the development and evaluation of systems pharmacology models[J]. Cpt Pharmacometrics &Systems Pharmacology, 2015, 4(2): 69.

[26]Gilks W R, Roberts G O, George E I. Adaptive direction sampling[J]. Journal of the Royal Statistical Society, 1994,43(1): 179－189.

[27]Liang F, Wong W H. Real-parameter evolutionary Monte Carlo with applications to Bayesian mixture models[J].Publications of the American Statistical Association, 2001,96(454): 653－666.

[28]Brooks S P, Roberts G O. Convergence assessment techniques for Markov chain Monte Carlo[J]. Statistics &Computing, 1998, 8(4): 319－335.

[29]马玉平，王石立，张黎. 针对华北小麦越冬的 WOFOST模型改进[J]. 中国农业气象，2005，26(3)：145－149.Ma Yuping, Wang Shili, Zhang Li. Study on improvement of WOFOST against overwinter of wheat in North China[J].Chinese Journal of Agrometeorology, 2005, 26(3): 145－149.(in Chinese with English abstract)