基于Realizable k-epsilon模型的水闸下游水流数值模拟

代 彬，陈章淼，周 维

(贵州省水利水电勘测设计研究院, 贵州 贵阳 550000)

水闸是渠道或河道工程中十分重要的水工建筑物，其主要作用是控制上下游水位与流量，可以用于挡潮、拦洪、蓄水、泄洪、冲沙、排涝等目的[1-3]。随着社会经济的发展，我国河道污染状况形势严峻，水闸也可用于阻挡上游的部分杂物，从而保证下游水体的水质。水闸流的水力分析一方面可以为水闸及其配套设施的设计与管理提供基础，另一方面也有助于了解水闸的设置与运行对河流的影响[4]。但目前，水闸流的研究范围主要集中于过闸水流，而水闸下游水流的研究成果则相对较少。水闸下游的水流特性可以引发河床的冲淤变化、影响下游水工建筑物、改变下游河道形态，因此其水力分析具有十分重要的现实意义。

水闸下游水流的特性分析可以采用统计分析法、经验公式法、物理试验法、数值模拟法[5]等。其中，统计分析法的操作方法相对简单，但对数据的依赖性较高；随着大数据、物联网以及神经网络等技术[6]的发展，未来可以成为非常重要的分析工具，但目前的数据储备状况尚不足以支撑准确的工程预测。经验公式法与统计分析法较为接近，主要是将实际案例的状况与一定的理论背景知识相结合，提出较为简单的公式；该方法可用于工程项目的粗略估算，但是精确度较低，未来可能被逐渐淘汰。物理试验法除却比尺问题外，一般被认为精确度较高，让是当前水力分析的最重要途径之一，但该方法需要的人力与时间成本较高。数值模拟法可结合以上各方法的优点，可以在保证一定精确度的基础上降低成本、提高效率，因此正逐渐成为水流特性研究的一种主流方式[7]。但是，不同的数值模型在不同的研究问题中具有明显不同的适用性，因此在应用之前，必须要进行模型的适用性分析和模型优选。数值模型中的湍流模型一般对模拟具有较大的影响，是数值模型不确定性的最主要来源之一，因此有必要对其进行详细研究。当前，最为常用的湍流模型为标准的k-epsilon模型，该模型可以求解湍流动能与湍流动能消散率两个变量，从而对整个模拟系统进行闭合。该模型具有较好的收敛速度与内存要求，精确度也一般满足工程要求。标准的k-epsilon模型实际在求解以上变量中采用了半经验的公式，因此其适用性可能在不同的条件下出现明显的差异。近些年出现的Realizablek-epsilon模型则可以在此方面对标准模型进行改进，它为湍流黏性增加了一个计算公式，也为耗散率的计算增加了新的传输方程，因此大幅降低了标准k-epsilon模型的经验性。截止目前，无论是在实际工程设计中还是理论研究中，基于Realizablek-epsilon模型的水闸流模拟几乎没有被报道过。鉴于此，以贵州省盘县鱼洞坝水利工程放空底孔为原型，采用Realizablek-epsilon模型进行三维数值模拟，并将模拟结果与标准k-epsilon模型的模拟结果和试验测量结果进行对比与分析，以分析该方法在水闸下游水流预测中的有效性。

1 方 法

1.1 控制方程

不可压缩流体的连续方程主要基于质量守恒定律，它可以表示为：

(1)

Navier-Stokes方程中的动量方程则主要基于动量守恒定律，它可以表示为：

(2)

式中：ρ代表密度；t是时间；Ui表示速度；xi与xj为坐标。式中p为压强，μ和μt分别代表分子黏性与湍流黏性。

1.2 标准k-epsilon模型

标准k-epsilon模型是河道水流模拟中最为常用的模型之一，它主要采用两个传递方程来描述湍流，一个是确定湍流能量的湍流动能方程，另一个是表达湍流动能的能量消散率的湍流消散方程。该模型可表达为[8]：

(3)

(4)

式中：k代表湍流动能；ε代表湍流动能消散率；μ1为层流涡黏系数；σk、C1ε和C2ε为模型常数。

1.3 Realizable k-epsilon模型

标准的k-epsilon模型具有一定的经验性，而Realizablek-epsilon模型则对其进行了改进。一方面它引入了一个更为合理的湍流黏度公式，同时它又使用了一个新的能量消散率传输方程，该方程不再基于假设而是由一个准确的涡流脉动传输方程推导而得[9]。该模型可表示为：

(5)

(6)

式中：Pk代表由速度梯度产生的湍流动能；Pb代表由浮力产生的湍流动能；YM是由于扩散产生的波动；Sk与Sε为参数；C3ε为模型常数。

1.4 模型设置

模拟主要以贵州省盘县鱼洞坝水利工程放空底孔为原型，而Demirel的水闸流试验[10]与该工程的布置形式基本一致，分别如图1与图2所示，且其所得测量结果均以无量钢化的形式表达，因此可直接采用该测量成果对模拟进行验证与分析。本次模拟主要在Linux系统下的开源计算流体力学平台OpenFOAM中进行，采用同系统下的前期处理软件Salome进行几何文件与计算网格的生成，并用后期处理软件ParaView进行数据提取，最后采用MATLAB程序对数据进行处理与分析。模拟中水槽长10 m、宽0.4 m、深0.6 m。闸门开启度(B0)为0.03 m，将此闸门开启间隙设置为速度入口，其速度(U0)为2 m/s，雷诺数为6×104。下游边界为压力出口，其水位控制为0.25 m。采用非结构化网格，其计算单元尺寸量级为0.001 m；时间步长为0.1 s,模拟计算到1 000 s；单元尺寸与时间步长对结果的影响可以忽略不计。模拟时长为360 s，之后水流基本保持稳定。

图1 鱼洞坝水利工程放空底孔布置形式

图2水闸流试验设置示意图

2 结果与讨论

2.1 自由水面

水闸下游水位是水闸流分析中最重要的参数之一，也是验证数值模型的最根本依据。由图3所示，k-epsilon和Realizablek-epsilon湍流模型所预测的水面线变化趋势均与实验数据保持一致，证明两者均可用于水闸流的模拟中，但是相对于k-epsilon模型，Realizablek-epsilon模型的模拟结果更为精确。

2.2 流速分布

水闸下游水流流速的测量与模拟结果如图4所示，各图分别代表不同水平位置处的流速分布，其中x+表示无量钢化的水平位置(x+=x/B0)，图中y+表示无量钢化的数值位置(y+=y/B0)，u+表示无量钢化的初始速度(u+=u/U0)。根据比较结果可知，两项模拟的结果均较接近于测量结果，但Realizablek-epsilon模型的模拟结果与实测数据具有更好的吻合性。

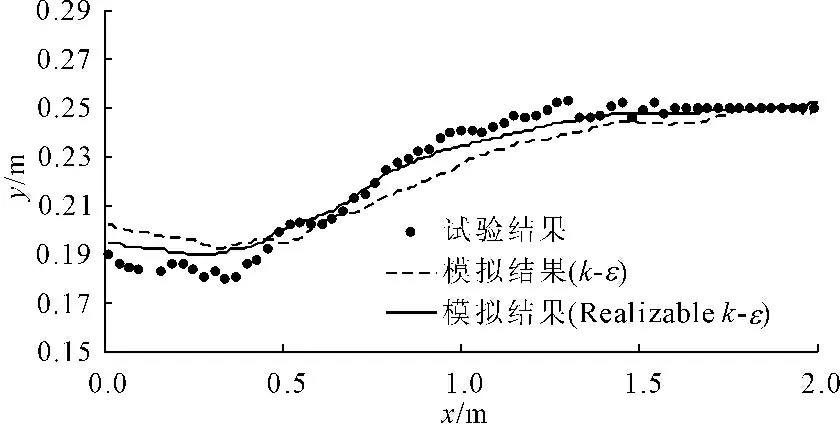
图3自由水面试验与模拟结果

2.3 误差原因分析

由模拟结果与实验数据的比较可知，k-epsilon和Realizablek-epsilon模型可以十分准确地计算水闸下游水流的自由水面与流速分布，但Realizablek-epsilon模型更为精确。模拟结果与实验数据的细小偏差可能由一下几个原因导致:首先，模型中的几个常数为经验参数，是由其它实验的结果而确定的，但这些参数的取值在不同问题中的适应性会略有不同，因此在以后的研究中可以通过修正这些参数来进一步提高模拟精度；其次，水闸流态是一种具有剧烈紊动性的水流，其流速分布会随时间轻微波动，而实验数据一般是用一个时间段内的平均值来表示最终的水力特性，因此数据统计操作可能是引起模拟与实验数据偏差的另一个因素。

图4流速试验与模拟结果

2.4 模型应用

采用经过验证的数值模拟法进行数值实验可以作为水闸流理论研究的重要工具。该方法在水闸流预测中的适用性已得到验证，因此在以后的研究中可以采用该模型对水闸流进行理论分析，例如水闸开口高度对自由水面的影响分析、水闸所处位置对水力特性的影响分析、入口水力条件与下游水位之间关系的分析等[11-13]。在实际水闸工程尤其是小型水闸工程应用中，流场分析大多还是基于经验法，而数值模拟的方法在水闸流分析中更为准确、全面、直观，因此可以在工程优化设计、安全分析、以及环境保护等实际工程应用中发挥重要作用[14-16]。例如，工程师可通过模拟来确定不同水闸开口高度所对应的下游水位及流速，从而根据实际需要来对水闸进行合理的设置；模拟可以确定不同工况下水闸所受压力，因此可以根据模拟结果来确定水闸设计标准，既保证工程安全又不造成材料浪费；模拟可以定性定量地显示出研究区域内各个位置的流速分布，因此结果可以用于确定水流对河岸河床的冲刷情况以采取相应的工程保护措施。贵州省盘县鱼洞坝水利工程的监测情况表明，应用Realizablek-epsilon模型所得的水面线形态与流速分布形式与实际状况基本一致，进一步证明了该模型的合理性。但模拟主要根据理想化的试验情景来设置，未来将对其进行拓展，考虑更多的因素，从而进一步提升其实际应用性。

3 结 论

采用Realizablek-epsilon模型对水闸下游水流进行了三维数值模拟，并将结果与标准k-epsilon模型结果和试验结果进行比较。模拟结果与测量的自由水面和流速分布基本一致，且优于k-epsilon模型，证明了该方法在水闸流水力特性计算中的有效性，为进一步提高当前的水闸流预测水平提供了信息与参考。Realizablek-epsilon方法可用于数值模拟试验中且成为水闸流理论研究中的可靠工具，并可以在工程优化设计、安全分析、以及环境保护等实际工程应用中发挥重要作用，但有必要对其进行拓展以考虑更多的影响因素，以提升其实际应用性。