全级配混凝土抗压强度尺寸效应及影响因素的统计分析
何 吉,徐小雪
(1.武汉大学 水资源与水电工程科学国家重点实验室, 湖北 武汉 430072;2.武汉大学 水工岩石力学教育部重点实验室, 湖北 武汉 430072)
工程中根据骨料的级配将混凝土分为一至四级,其中四级配混凝土的骨料粒径包含5 mm~20 mm、20 mm~40 mm、40 mm~80 mm、80 mm~150 mm四个完整等级,因此四级配混凝土也称为全级配混凝土[1]。全级配混凝土是重力坝、拱坝等大体积水工建筑物的核心建筑材料,其强度直接影响建筑物的稳定与安全,因此研究全级配混凝土的强度特性具有重要的科学意义和工程价值[2-3]。
全级配混凝土的强度一般通过物理试验测定。试验中为了减少骨料不均匀分布对结果的影响,通常将试件尺寸至少取为最大骨料粒径的3倍,即达到450 mm[4]。由于试验难度大、设备要求高,较大的试件尺寸极大地增加了试验成本,仅有少数重点工程才能进行全级配混凝土试验。因此设计中一般采用剔除拌合物中超过40 mm的大骨料,成型150 mm大小的湿筛混凝土试件进行小尺寸试验,并以此结果进行建筑物的设计和安全评价。如何采用湿筛小试件的试验结果来推测全级配混凝土的力学性能,一直是工程界和学术界普遍关心的问题[5-6]。
但是全级配大试件与湿筛小试件的强度特性差异较大,即存在明显的尺寸效应。据统计,两者的轴拉强度比值约为0.45~0.88,劈拉强度比值约为0.74~0.91,抗压强度比值约为0.70~1.09[7-8]。美国胡佛大坝的研究表明Φ18英寸×36英寸(约Φ450 mm×900 mm)圆柱体试件的抗压强度与Φ6英寸×12英寸(约Φ150 mm×300 mm)圆柱体试件抗压强度比值约为0.838[1];三峡工程的研究表明Φ450 mm×900 mm圆柱体试件与Φ150 mm×300 mm圆柱体试件抗压强度比值为0.90~1.02(28 d)、0.90~0.99(90 d);450 mm立方体试件与150 mm立方体试件劈拉强度比值为0.82~0.98(28 d)、0.80~0.87(90 d);Φ450 mm×900 mm圆柱体试件与Φ150 mm×300 mm圆柱体试件劈拉强度比值为0.75~0.85(28 d)、0.82~0.83(90 d)[9]。显然,强度比值与荷载形式、试件形状、龄期等影响因素有关,甚至出现大于1的现象。国内外学者从试件缺陷、骨料尺寸、骨料比表面积、破坏模式、试验条件等方面进行了研究[10-19]。此外,特别针对强度比值大于1的现象,从高频振捣对含气量的影响[17-18]、全级配与湿筛混凝土的砂浆—骨料界面差异[20]、试件受压面的减磨影响[9]等方面进行了研究。然而,已有的研究成果对于强度比值的设计取值及影响条件尚未达成一致的结论,这对大体积水工建筑物的设计、施工以及安全评价产生了极大影响。
目前常用的研究方法有理论分析、数值模拟以及数学统计。
(1) 理论分析方法是从能量、分形特性等角度分析混凝土的强度,通过实验修正,得到试件尺寸与强度比值的经验公式[21]。主要理论有Weibull脆性破坏统计理论[22]、基于能量释放理论的Bazant尺寸律理论[23]以及基于分形的Carpinteri尺寸律理论[24]。郑丹等[7]结合混凝土在不同荷载下的裂纹扩展模式,对Bazant断裂力学尺寸律理论进行了修正,得到了尺寸效应系数的经验公式。这些经验公式中通常假定较多,使用条件严苛,公式繁琐,难以被工程人员广泛采用。
(2) 数值模拟方法是对混凝土中砂浆、骨料及界面进行离散,建立细观尺度下的混凝土破损数值分析模型,通过数值模拟得到混凝土大试件的强度。Wang X F等[25]采用粘结单元方法,对大尺寸混凝土试件的破裂过程进行了模拟,建立了混凝土强度数值分析模型。但是数值模拟方法的操作复杂,建模及计算周期较长,并且如何准确标定计算参数是一个难题,不利于工程人员掌握。
(3) 数学统计方法是基于大量工程的试验数据,采用概率理论分析混凝土的强度比值,建立试件尺寸与混凝土强度之间的统计规律。杨忠义[9]采用溪洛渡与三峡工程的试验成果,统计了抗压强度比值的变化范围。邓宗才[1]采用三峡工程的试验数据,得到了抗压强度比值随龄期变化的经验公式。数学统计方法的本质是工程类比以及概率分析,因此概念明确、方法简单、经验丰富,容易被工程人员接受,其成果具有较好地工程应用前景。
本文将采用数学统计方法,重点针对混凝土的试件形状、龄期等影响因素,研究单轴受压荷载条件下混凝土强度的尺寸效应。
1 抗压强度比值的总体分析
将11个工程共137组全级配混凝土的试验数据汇总于图1,数据来源见图1中X轴所示的各工程[1,5-10,26-35]。

图1试验数据汇总
由图1可见,抗压强度比值最小为0.460,最大为1.210,平均为0.815,方差为0.026。当采用湿筛小试件的试验结果推测全级配混凝土的抗压强度时,如果取抗压强度比值的最小值计算,则得到的全级配混凝土抗压强度偏低,造成安全冗余偏大,经济成本偏高;如果取最大值计算,则结果偏大,造成强度预估不足,安全性偏低;如果取平均值计算,由于图中各点的离散性较大(方差较大),则结果偏差较大。
2 抗压强度比值的可靠性取值
由于上述最小值、最大值以及平均值在工程中均应用不便,下文将采用可靠性理论[35-39]来分析抗压强度比值。在可靠性理论中,混凝土的可靠度采用强度保证率来表示。工程中不同部位的混凝土具有不同的保证率要求,如水工大体积结构一般采用80%保证率,水工钢筋混凝土结构常采用90%保证率,薄壁结构或者重要部位宜采用95%保证率[40]。本文将可靠性理论从强度引入强度比值,采用图1中的试验数据计算具有80%、85%、90%、95%保证率的抗压强度比值,计算过程如下:
(1) 选取图1中立方体试件对应的72组试验数据,绘制抗压强度比值的柱状图,并拟合成概型分布曲线见图2。由图2可见,抗压强度比值具有服从正态分布的可能,平均值为0.843,方差为0.0522。

图2抗压强度比值的累积分布直方图及正态曲线拟合
(2) 假设随机变量β(抗压强度比值)服从正态分布N(0.843,0.0522),并采用K-S检验方法按显著性水平α=0.05进行非参数检验。
K-S检验是基于累积分布函数检验某个经验分布是否符合某种理论分布的经典方法[41]。该方法的基本理论为:令Sn(β)是一个容量为n的简单子样的经验分布函数,F(β)为所假设的总体分布函数,式(1)为检验统计量。基于柯尔莫哥洛夫定理[41],对于任意λ>0,满足式(2)。假设总体中变量β服从连续分布函数F(β),该假定记为H0。根据样本计算Sn(β)和统计量Dn,按照显著性水平α及样本容量n查阅柯尔莫哥洛夫分布的分位数表[41]得到D(n,α)。若D(n,α)大于Dn,则接受H0,即假设成立,总体变量服从假设的分布形式。
(1)
(2)

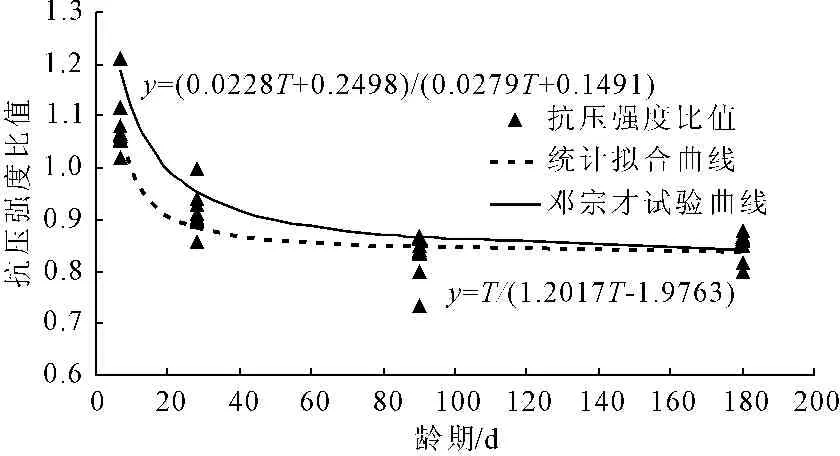
由式(1)可得统计检验量Dn=0.077。以显著性水平α=0.05,样本容量为n=72,查阅柯尔莫哥洛夫分布的分位数表[41]可得0.154 (3) 由正态分布查表[41]可得保证率为80%、85%、90%、95%对应的抗压强度比值如表1所示。 表1 不同保证率的抗压强度比值 目前混凝土湿筛试验的试件形状主要有两类标准[42]:立方体(150 mm×150 mm×150 mm)、圆柱体(Φ150 mm×300 mm)。这两类试件的试验结果存在显著差异,通常认为圆柱体试件与立方体试件的抗压强度比值约为0.7~0.8[40],影响因素主要有试件高径比、环箍效应、混凝土强度等[43]。全级配混凝土同样存在圆柱体(Φ450 mm×900 mm)与立方体(450 mm×450 mm×450 mm)两类试件,两者的强度差异是否仍为0.7~0.8,这是一个亟待明确的问题。 表2列出了溪洛渡[32]和二滩[29]水电工程采用不同试件形状时全级配混凝土大试件与湿筛混凝土小试件之间的抗压强度比值。由表2可见,立方体试件的平均值为0.847,圆柱体试件的平均值为0.560,说明不同的试件形状能够引起不同程度的尺寸效应,且圆柱体的尺寸效应大于立方体。通过简单计算,可得全级配圆柱体试件与立方体试件的强度比值约为(0.7~0.8)×0.560/0.847=(0.463~0.529)。由于数据有限,上述结果无法采用可靠性理论进行分析,无法得到基于保证率的结果,但是足以说明试件形状对尺寸效应的影响不容忽视。此外需要说明的是:由于图1中圆柱体试件的试验数据相对较少,因此表1中的结果由立方体试件得到,即该表仅适用于立方体试件;圆柱体试件对应的结果可以通过表1中的数据乘以系数(0.463~0.529)的方式换算得到。 表2 不同试件形状的抗压强度比值 注:表中抗压强度比值,立方体试件以150 mm×150 mm×150 mm的强度为基准,圆柱体试件以Φ150 mm×300 mm的强度为基准。 根据现有的研究成果[40],通常湿筛混凝土的强度在7 d内上升较快,之后减缓,28 d后趋稳。全级配混凝土强度的发展规律与湿筛混凝土基本一致[1],但是两者的抗压强度比值随龄期的变化规律则不同。 从图1中选取了溪洛渡[30,32]、锦屏一级[28]水电工程共8组试验数据,绘制了抗压强度比值随龄期变化图,如图3所示。由图3可见,龄期对尺寸效应的影响显著,抗压强度比值在7 d时最大,7 d~28 d下降显著,28 d~180 d基本稳定。 图3抗压强度比值随龄期变化图 (3) 同时拟合了湿筛混凝土抗压强度(fc)与龄期(T)的关系式: (4) 还将式(3)除以式(4),得到了抗压强度比值随龄期变化的表达式: (5) 图3中实线为式(5)对应曲线,可见该式能够反应溪洛渡、锦屏一级这8组试验数据的整体变化规律,但是在7 d~28 d下降偏缓。 借鉴式(3)、式(4)的表达形式,假定全级配混凝土抗压强度(y)与龄期(T)的关系式为y=T/(aT+b),采用最小二乘法拟合图3中数据,可得a=1.2017,b=-1.9763,即 (6) 图3中虚线为式(6)对应曲线,可见该式在7 d~28 d下降明显加快,基本接近试验数据的下限,说明更偏于安全。工程中可以采用式(6),基于湿筛混凝土的试验结果来推测不同龄期时全级配混凝土的抗压强度。 由于试验数据有限,骨料、水灰比、掺合料等因素的影响无法充分考虑,所以并不能够说明式(6)更能反应抗压强度比值随龄期的变化规律,仅仅为工程人员增加了一种参考。此外,图3中部分试验数据在90 d时明显偏小,甚至小于180 d的数值,其原因仍有待进一步研究。 本文根据11个工程共137组试验数据,运用数学统计原理分析了全级配混凝土大试件与湿筛混凝土小试件之间抗压强度比值的分布规律及影响因素,为如何采用湿筛小试件的试验结果推测全级配混凝土的抗压强度提供了量化依据,为工程的设计、施工以及安全评价提供了参考。
3 试件形状对抗压强度比值的影响

4 龄期对抗压强度比值的影响
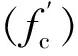
5 结 论

