考虑黏性成分时的渗流固结理论及其在工程中的应用
齐 龙,李志华,王述红
(1.东北大学 资源与土木工程学院, 辽宁 沈阳 110819; 2.中建五局土木工程有限公司, 湖南 益阳 413000)
自Terzaghi一维固结理论提出的半个多世纪以来,人们已有大量的工程实践和改进方法,但是问题仍然没有完全解决。在实际工作中常常发现Terzaghi一维固结理论计算的结果与实测值存在较大差距[1],传统的固结理论是在岩土工程中应用范围最广的理论之一[2]。众多学者针对固结度理论值与实际值相差过大,已展开了大量的研究工作[3-13]。一维固结又称为单向固结,是指土体荷载作用下产生的变形与孔隙水的流动仅发生在一个方向上的固结。严格的一维固结只发生在室内有侧限的固结实验中,在实际工程中并不存在[14]。但是当大面积均布荷载作用下的固结可近似为一维固结问题[15]。太沙基(1924)建立了如图1所示的固结模型,图中,整体代表一个土单元,弹簧代表土骨架,水代表孔隙水,活塞上的小孔代表土的渗透性,活塞与筒壁之间假定为完全光滑的。

图1经典渗流固结模型
不难理解,太沙基先生采用弹簧代替土骨架实际上是将土体看成完全弹性体,也就是采用此模型的前提是其必满足胡克定律。胡克定律(Hooke's law)是力学弹性理论中的一条基本定律,表述为:固体材料受力之后,材料中的应力与应变(单位变形量)之间成线性关系。满足胡克定律的材料称为线弹性或胡克型(Hookean)材料。实际情况中,即使是工程特性较为理想的砂土也并非胡克型材料,而可塑性强、流变性大的黏土就更不可能符合胡克定律。因此,以经典的太沙基渗流固结理论计算黏土地区的固结沉降势必造成非常大的误差。
1 对经典的太沙基一维渗流固结理论的修正
1.1 一种新的渗流固结物理模型
针对经典的太沙基渗流固结理论用于黏土地区时的不足,本文从工程实际土质情况出发,在经典的太沙基一维渗流固结模型中考虑黏滞效应,提出了一种新的渗流固结模型。为了形象的阐明饱和黏性土的渗流固结过程,这里借助一个弹簧-黏滞壶-透水活塞的力学模型进行说明见图2。
在一个装满水的圆筒中,上部安置一个带细孔的活塞。此活塞与筒底之间安装一个弹簧和一个黏滞壶,以此来模拟饱和黏性土层。弹簧可以看做土的骨架,黏滞壶代表黏性效应,模型中的水相当于土体孔隙中的自由水。则:
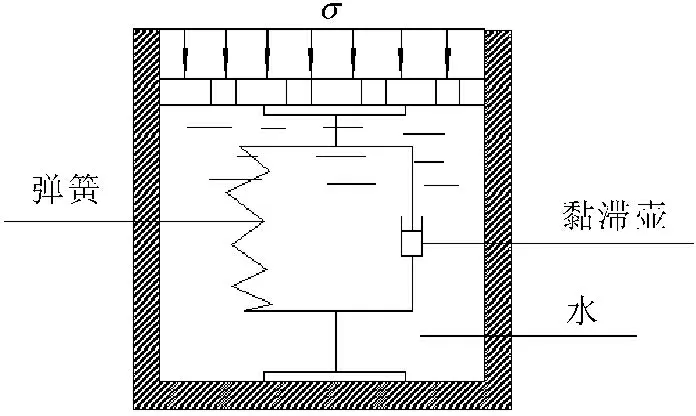
图2考虑黏性成分的渗流固结模型
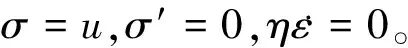

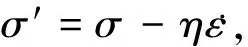
由此可见,饱和黏性土体的渗流固结,就是土中的孔隙水压力u消散、转移为有效应力与黏性力之和的过程。
1.2 基于新模型对经典一维渗流固结方程的修正
假设饱和黏性土土层厚度为2H,土层上下两面为透水层,作用于土层顶面的竖直荷载无限广阔分布,在任一深度z处,取一微单元体进行分析。
令微元的固体部分体积为1,在单位时间内,这个微元体内挤出的水量q,等于微元体内孔隙体积的压缩量V。设这个微元体底面的渗流速度为v,顶面的渗流速度为则:
(1)
(2)

(3)
(4)
孔隙体积的压缩量:
V=dVv=d(nV)
(5)
(6)
对于饱和土体,在单位时间dt内,这个微元体内挤出的水量q,等于微元体内孔隙体积的压缩量V,得到:
(7)
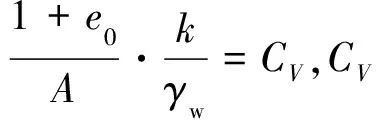
(8)
根据Kelvln模型(弹簧与黏滞壶并联的黏弹性模型)的积分公式:
(9)
式中:E为弹性模量;η为黏滞系数;e为自然对数的底。
则:
(10)
根据图3所示的边界条件(可压缩土层顶底面排水条件)和初始条件(开始固结时的附加应力分布情况)
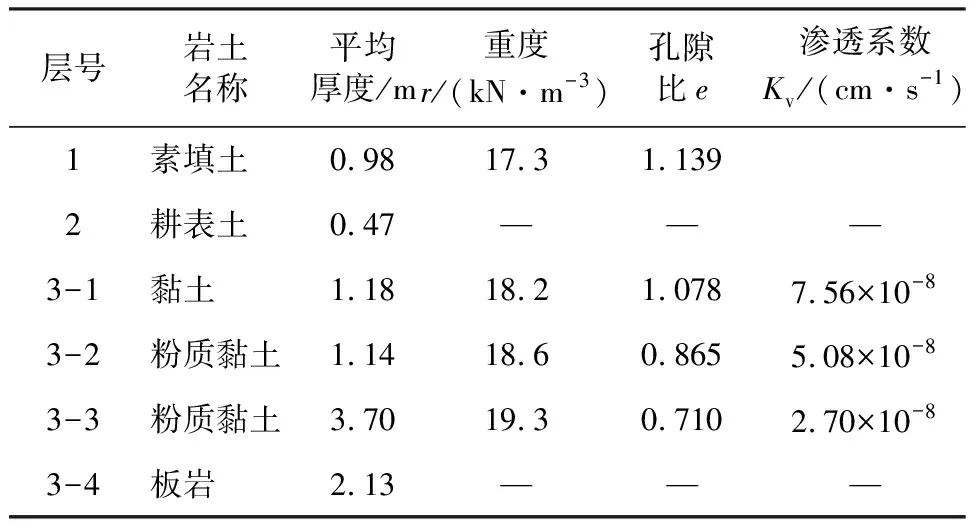
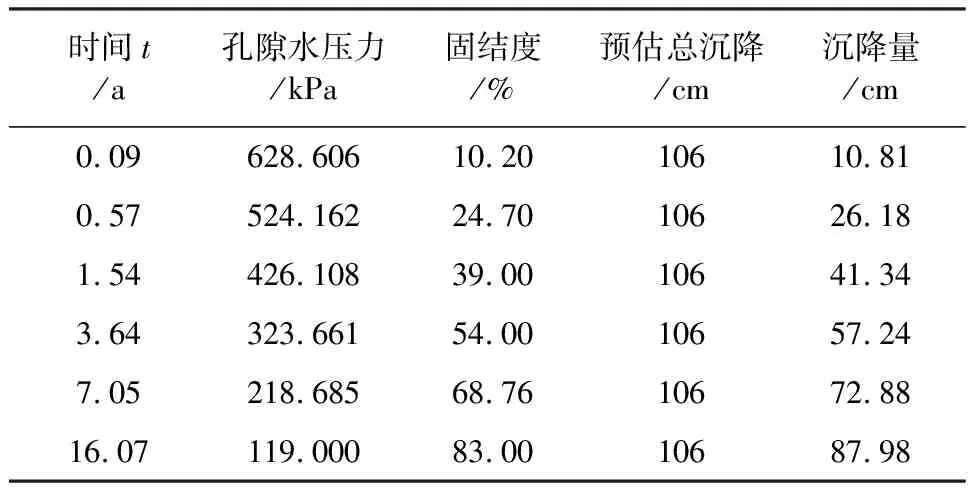
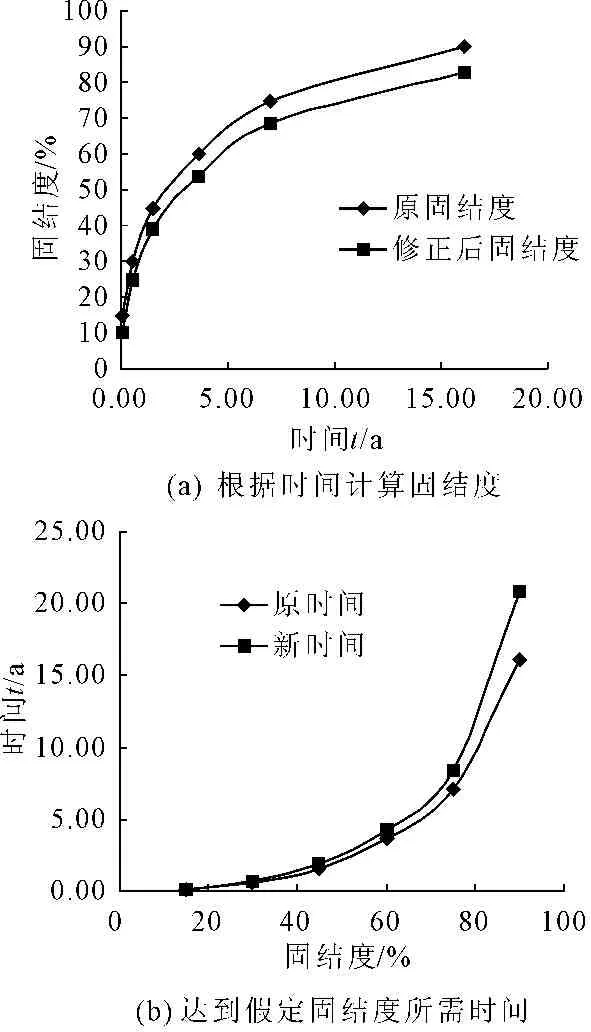
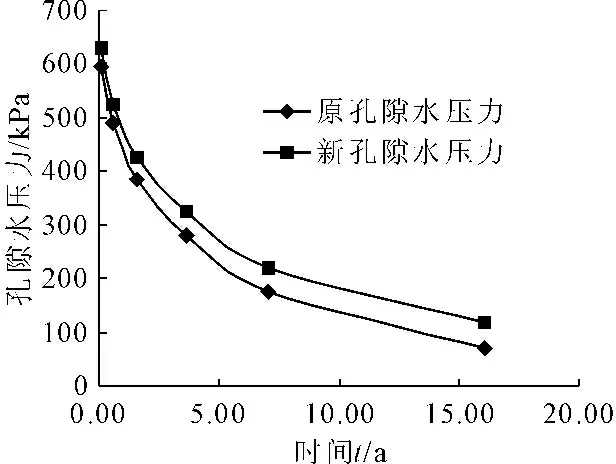
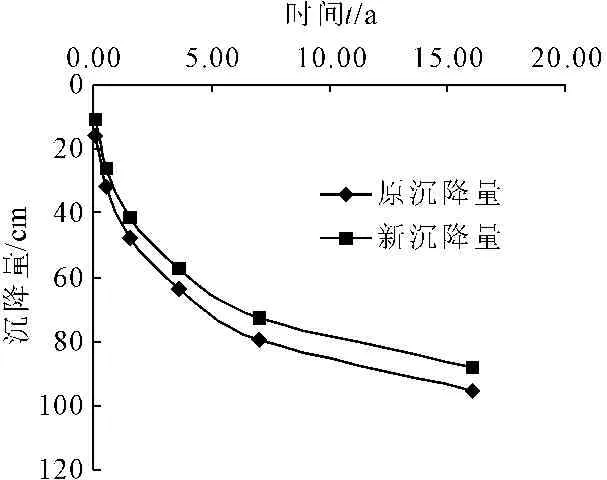
z=0,u=0,(0 t=0,u=σ,(0≤z≤2H) 可得: (11) 则根据式(11)可以计算图3中任意点及任一时刻的超静孔隙水压力u(z,t)。 通过上述理论可以实现: (1) 已知土层的最终沉降量,求某一固结时间内已完成的沉降。 (2) 已知土层某一固结时间的沉降,去预测最终沉降。 图3饱和土层的固结 (3) 已知最终沉降量,求完成某一沉降量所需要的时间。 (4) 已知某一沉降量,去预测最终沉降量所需要的时间。 应当指出,修正后的太沙基一维固结理论是在经典的太沙基一维固结理论基础上实现的,所以,二者有一些共同的假定条件:(1) 土体是完全饱和的土体;(2) 土体是均质的;(3) 土颗粒与孔隙水在渗流固结过程中的本身是不发生形变的;(4) 土中水的渗流服从于Darcy's Law;(5) 土中的水渗流与土体的变形发生在单一方向;(6) 外部荷载是一次性瞬时施加的荷载;(7) 在饱和土体固结过程中,土体的压缩系数a是一个不变的常数;(8) 在饱和土体的固结过程中,土体的渗透系数k是一个不变的常数;(9) 土体的固结变形服从小变形假定。 益阳东部新区外环路位于益阳东部新区西部,外环路(起点接G319国道,终点接衡泉公路)是以鱼形山水库为中心的一条环型道路。根据本项目在益阳东部新区路网中的规划定位,本项目道路为城市主干道,位于益阳软弱土区域,施工困难,特别是不均匀沉降的控制和软弱地基的处理,目前还没有发现益阳地区这类软弱土体不均匀沉降控制和城区主干道改扩建的相关文献资料记录,为保证项目顺利按期高质量完成,急需有针对性地开展相关研究。 本项目位于益阳东部新区,是联系外环路东西向交通的一条生态高效、绿色经济的具有国际领先水平的城市干道,路线起于高新大道与G319国道平交处,起点桩号K0+000,路线呈南北向,基本沿现状地方道路围绕鱼形山水库,途经沧水铺三眼、花桥、双板桥、鱼形山水库东南侧外缘、荷叶塘、四方山村,终于阳雀坪附近的现状衡泉公路,终点桩号K13+541.436,路线全长约13.541 km,途经线路现状大部分有机耕水泥道路相通,交通较一般,局部较差。拟建主线下穿现状石长铁路、规划益宁城际轻轨、在建石长铁路复线,并与多条规划公路及内环路交汇,项目所在地交通前景较好。主线采用城市I级主干道标准,设计时速60 km/h。地质资料见表1、表2。 表1 地质资料 表2 时间因子 因素填土与耕表土在施工时挖除,故选择3-1层土至3-3层土进行计算。深度h为6 m,黏土地基的孔隙比e1=1.078,e2=0.710。基地应力按照《公路路基设计规范》[16](JTG D30—2015)中规定的标准轴载BZZ-100采用,即作用在车轮上的荷载P=25(100/4)kN,轮胎接触压力p=700 kPa, 这里假定标准轴载大面积均匀分布。6 m深度处的附加应力为9.26 kPa。 (1) 地基沉降量估算 (2) 计算附加应力比值 (3) 假定地基平均固结度分别为15%、30%、45%、60%、75%、90%;按照经典的太沙基渗流固结理论公式(12)计算得到时间因子如下: (12) (4) 计算相应时间t ① 地基土的压缩系数 ② 渗透系数换算 渗透系数用3-1层到3-3层的加权平均值: Kv=2.77×10-8cm/s 将渗透系数单位进行换算为 k=0.873 cm/a ③ 计算固结系数 (4) 表3为计算相应数据。 表3 经典理论计算数据 在某一荷载作用下,对某一深度z处,经过时间t后土体固结过程完成的程度叫做固结度,通常用U表示。土体在固结过程中完成固结变形和土体抗剪强度的增长均与固结度有关。饱和黏性土土体中某点的固结度可表示为 (13) 为方便进行对比,取上面的地基平均固结度分别达到假定固结度时所对应的时间,以考虑黏性成分时的太沙基渗流固结理论对固结度进行反算(见表4),并计算相应的超孔隙水压力和沉降量的值,与经典理论计算结果进行对比分析,分析结果见图4、图5、图6。 表4 修正后渗流固结理论计算数据 图4固结度与时间的关系曲线 通过对比分析图4可得到,在时间为0.09 a时,太沙基经典理论计算的固结度为15%,而新理论计算的固结度为10.2%;完成初步固结(15%)所需的时间,按照经典理论计算需要0.09 a,而新理论计算0.14 a;而最终完成固结时间新旧理论计算结果的差别就更为明显,原理论计算需要20 a,而新理论计算则需要25 a,其结果相差25%左右。按照经典的太沙基渗流固结理论计算得到的固结度偏高,在同样的时间内经典理论过高的计算了固结度。黏土的固结越到后期会越慢[17],而修正后的一维渗流固结理论更能符合这一特点。 从图5可以看出,孔隙水压力均随着时间的推移而消散,但是在同样的时间内,修正后渗流固结理论计算的孔隙水压力消散量要比经典的渗流固结理论消散量要小,这是因为经典的太沙基渗流固结理论没有考虑黏性成分对孔隙水压力消散影响的结果[18]。 图5孔隙水压力与时间的关系曲线图 图6沉降量与时间的关系曲线图 从图6中可以看出,当时间为5 a时,原理论计算沉降量为75 cm;而新理论计算的沉降量为63 cm;当沉降量达到80 cm时,按照原理论计算需要7 a,而新理论则需要用12 a左右。 (1) 针对经典太沙基渗流固结理论于黏性土计算的不足,提出一种新的物理模型,并以模型为基础,对经典的太沙基一维渗流固结方程进行了修正。 (2) 在修正后的渗流固结理论中,跟经典的太沙基一维渗流固结理论相比,同样的时间内,超孔隙水压力消散的力度更小;随着时间的推移,消散速度越来越慢。 (3) 在同样的时间内,修正后的渗流固结理论计算的沉降量要小于经典的渗流渗流固结理论计算结果,但达到最终沉降时,修正后的渗流渗流固结理论所需要的时间要长于经典的渗流渗流固结理论。

2 工程概况

3 修正后的理论与经典理论计算结果对比分析
3.1 经典的太沙基渗流固结理论计算
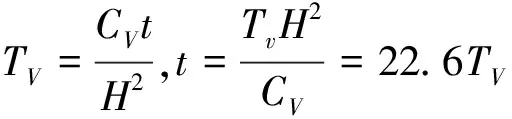

3.2 修正后太沙基渗流固结理论与经典理论计算结果对比
4 结 论

