波箔气体轴承支承的转子非线性振动的研究

陈诚，马希直

(南京航空航天大学 机电学院，江苏 南京 210016)

0 引言

波箔气体轴承作为一种新型的气体轴承，由于其在稳定性和承载能力方面的优越性，已经越来越多地应用于各种微型燃机中。但国内关于气体轴承转子在高速下的运转性能，尤其是非线性振动特性的研究还很欠缺。此前，Kyuho Sim和Yong-Bok Lee等[1]建立了波箔受力模型并用之求解箔片静刚度。P.Bonello 和H.M.Pham[2]研究了密封气膜力激励下的高速离心压缩机Jeffcott转子的非线性振动和分岔现象，给出了基于转速和压差参数变化的转子横向分岔图。Yong-Bok Lee[3]等对弹性波箔轴承支承的柔性转子系统的动力学行为进行了数值分析，并且分析了弹性摩擦力对转子动力学运动的影响。徐方程[4]分析了基于库伦摩擦效应的气体轴承-转子系统的静特性和稳定性，并对轴承性能和转子动力学特性进行了实验研究。

本文主要针对波箔气体径向轴承支承转子的运动情况，建立转子局部受力模型，模拟在气膜力和摩擦力共同作用下转子的振动情况。对比在不同转速下的转子轴心轨迹和Poincaré截面图，观察转子在升速过程中出现的混沌运动特征，据此总结出转子非线性运动的规律，为转子动力学的后续研究提供理论依据。

1 转子受力模型

以波箔径向轴承支承的转子段为例，建立其运动模型。该段的横截面如图1所示。图中φ表示轴颈相对于坐标轴的转角，h为气膜厚度，ω表示轴颈转速。转子集中质量为m，x方向和y方向的轴承主刚度分别为kx和ky，交叉刚度为kxy，轴承主阻尼分别为cx和cy，交叉阻尼为cxy。

1.1 波箔轴承气膜力

气体介质在轴承间隙中的流动服从非定常可压缩流体Reynolds方程：

(1)

式中，Rb为轴承内径，Rj为转子直径，e和θ分别为轴颈平衡位置的位移和转角，ε为轴颈偏心率，φ为周向位置坐标，z为轴向位置坐标，P为气膜压力，ρ为气体密度，μ为气体粘度；Uj=Rjωj，Ub=Rbωb，ω=ωj+ωb，轴承间隙c=Rb-Rj。

由于轴承段集中为点质量，实际上轴承段的宽径比<1，因此可以用短轴承假设模型，该模型下轴向压力梯度忽略不计。此外，由于波箔轴承工作过程中气膜形成前后气体的总体积变化均不大，因此可以忽略气体可压缩性的影响。由此简化的轴承气膜力的Reynold方程可以表示为：

(2)

在假设轴承泄油端压力为0的条件下对方程(2)沿轴承表面积分，得到非线性气膜力表达式：

(3)

其中:

式中：R表示该段半径，l表示长度。通过坐标变换，可将径向和周向的气膜力分量Fr和Ft变换到x、y方向上，为：

(4)

得到气膜力在x、y两个方向的分量为:

(5)

1.2 波箔轴承箔片摩擦力

波箔轴承的箔片几何结构如图2所示。

图2 波箔片几何结构示意图

图中波箔片在载荷p的作用下会发生变形，由于箔片一端固定在轴承壳体上，另一端自由的搭在轴承内表面上，因此在受载荷作用时，自由端处箔片会向两侧滑移。滑移时的摩擦力模型如图3所示。

如果相邻两个箔片受到的压力分别为Wi和Wi+1，并在竖直方向产生vi和vi+1的位移，则箔片左右两边的支反力NL和NR分别为：

图3 波箔片摩擦模型示意图

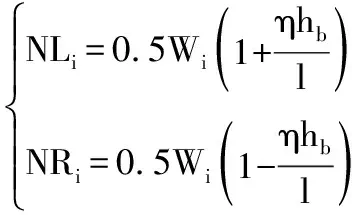
(6)

则平箔片和波箔片之间的摩擦力为ηWi,波箔片与轴承壳体之间的摩擦力为u(NRi+NLi+1)，η和u均为摩擦系数。因为载荷均布，因此每个节点的W相等，因此总摩擦力在x,y方向上的分力分别为:

(7)

1.3 转子局部运动微分方程

设转子的位移分别为x、y，则单元的局部运动微分方程为:

(8)

式中，Fx、Fy为气膜力分量，Px、Py为箔片摩擦力分量。

2 数值计算方法

对于如式(8)这样含非线性项的非齐次常微分方程组，采用4阶变步长Runge-Kutta法对其进行求解。该方法求解思路如下：高阶常微分方程的初值问题可以化为一阶微分方程组的一般形式:

(9)

在计算函数值Y时，首先分别求出从Y(t0)点出发时Yn的值,其中h为计算步长。则4阶Runge-Kutta法的计算公式为:

(10)

如上所述，下一个函数值Yn+1由当前的值Yn加上步长h与估算斜率的乘积共同决定，估算斜率是K1，K2，K3，K4的加权平均。其中，K1是时间段开始时的斜率；K2是时间段中点的斜率，通过欧拉法采用斜率K1来决定Y在点tn+h/2处的值；K3也是中点的斜率，是采用斜率K2来决定Y值；K4是时间段终点的斜率，其Y值由K3决定。则每步的误差是h5阶，总的累计误差为h4阶。

3 转子非线性动力学计算结果

运用MATLAB软件编制4阶变步长Runge-Kutta法的求解程序，对转子的运动进行数值求解。由于波箔轴承是动压轴承，工作时环境压力为1个大气压。此外，波箔轴承工作时是由气膜支承转子，因此转子在工作过程中的温升较小，波箔轴承支承的转子系统的工作温度一般在-20 ℃～100 ℃之间，本文取其中间值40 ℃时的气体粘度、气膜刚度和阻尼。系统的一阶临界转速经预先计算得出:ω1=5 582 r/min。

图4为转速ω=3 500 r/min时转子的轴心轨迹图和Poincaré截面图。由图可知，当转子在亚临界转速区(ω<ω1)运转时，轴心轨迹表现为一系列拟周期分布的近似椭圆形。Poincaré截面图上呈现出孤立的周期吸引子。此时转子运动的实质是在启动过程中由于波箔片与轴承内壁的非线性摩擦阻力引起的拟周期运动。该转速下转子还未完全启浮，在运动方程中摩擦力起主要作用。

图4 转速为3 500 r/min时转子的响应

图5为转速ω=5 500 r/min时转子的轴心轨迹图和Poincaré截面图。由图可知，当转子在临界转速区(ω≈ω1)运转时，轴心轨迹表现为振幅较小的椭圆形。Poincaré截面图上呈现出构成封闭曲线的周期吸引子，此时转子响应为规则的周期运动。在该转速下运动时，摩擦力恒定，轴承气膜力起主要作用，转子运动趋于平稳，非线性特征很不明显。

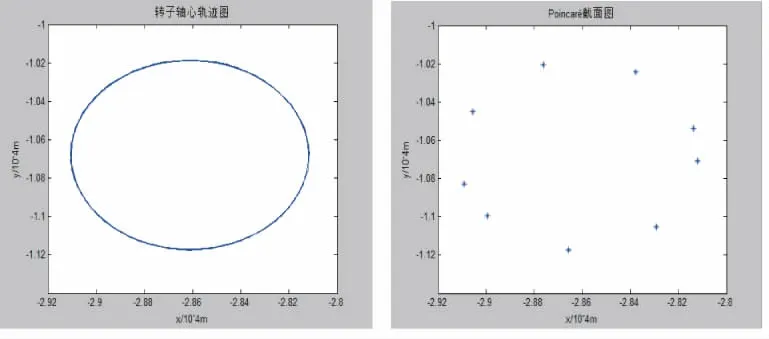
图5 转速为5 500 r/min时转子的响应

图6为转速ω=9 500r/min时转子的轴心轨迹图和Poincaré截面图。由图可知，当转子在3倍临界转速附近(ω≈3ω1)运转时，轴心轨迹表现为围绕着极限环的一系列近似的椭圆形，转子在一个有一定宽度的空间环带中运动。Poincaré截面图上呈现出接近封闭曲线的周期吸引子，此时转子响应表现出典型的倍周期分岔特征，在耗散系统中可以充分认定其为拟周期运动。在该转速下运动时，摩擦力恒定，轴承气膜力起主要作用，但气膜力方程的非线性特征开始体现。

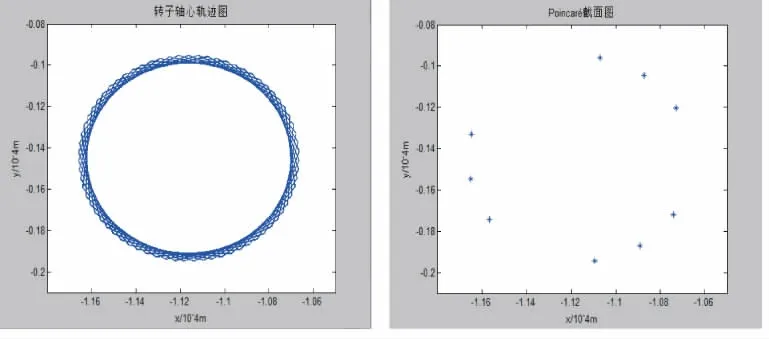
图6 转速为9 500 r/min时转子的响应

图7为转速ω=15 000 r/min时转子的轴心轨迹图和Poincaré截面图。由图可知，在转子出现倍周期分岔后继续升速过程中，轴心轨迹的分岔现象不断增强，空间环带的宽度不断增大，极限环的边界也不断缩小。Poincaré截面图上也呈现出更为密集的周期吸引子，此时转子响应表现为强烈的拟周期运动。该转速下轴承气膜力依旧起主要作用，非线性特征十分明显。

图7 转速为15 000 r/min时转子的响应

图8为转速ω=20 000 r/min时转子的轴心轨迹图和Poincaré截面图。由图可知，在典型的超临界转速区，转子轴心轨迹开始出现不规则特征，极限环的形状开始变化，由椭圆形变为不规则形状，同时振幅也相应增大，运动在保留拟周期特征的同时开始表现出混沌特征。Poincaré截面图上也开始出现典型的具有自相似特征的混沌吸引子，此时转子响应为拟周期运动和混沌运动的组合。该转速下平箔片与波箔片、平箔片与轴颈之间的两种摩擦为摩擦力的主要形式，其与轴承气膜力同时作用，非线性特征更加强烈。

图8 转速为20 000 r/min时转子的响应

图9为转速ω=2 2000 r/min时转子的轴心轨迹图和Poincaré截面图。由图可知，在转子开始出现混沌运动后继续升速的过程中，拟周期特征开始减弱，混沌特征不断增强，轴心轨迹的环带外边界消失，极限环也不再显现，振幅继续增大。Poincaré截面图上的混沌吸引子的分布开始离散，不再具有自相似特征，此时转子表现为典型的混沌运动。转子气膜力和摩擦力的非线性同时作用，转子的运动开始不可控。

图9 转速为22 000 r/min时转子的响应

图10为更高转速下转子的轴心轨迹图。从转子出现典型的混沌运动开始继续升速，轴心轨迹变得更加不规则，混沌特征更加显著，振幅也继续增大。同时由于混沌吸引子更加离散，在Poincaré截面图的坐标系中无法显示。此时转子表现为完全混沌状态，气膜力和摩擦力的作用无法顺利区分。在转子达到90 000r/min以上时，振幅开始超过初始气膜厚度，波箔片将于轴瓦表面贴合，波箔轴承无法正常工作。

图10 转速为27 000 r/min和50 000 r/min时转子的响应

4 初步试验验证

实际运转时的转子非线性现象受许多因素影响，除了本文所分析的气膜力与箔片摩擦外，转子不对中故障、轴承套碰磨等也会引起非线性振动，因此，要对转子非线性进行系统化的试验研究是十分困难的。国内目前对气体轴承转子的非线性试验研究仍处于探索阶段。

本文对所分析转子在20 000r/min以下运转时的轴心轨迹作了试验测试，试验装置如图11所示。

图11 波箔轴承-转子系统实验台

图12为转子转速分别为5 000r/min、10 000r/min、15 000r/min、20 000r/min时测试并整理得到的转子轴心轨迹。由测试结果可以看出，随着转子转速的上升，转子的非线性特征渐趋明显，试验结果与理论计算值较为接近。限于试验条件，本文对于转速更高时的转子运动规律尚未进行进一步验证，这也是国内气体轴承与转子动力学等学科所需研究的一项重要课题。

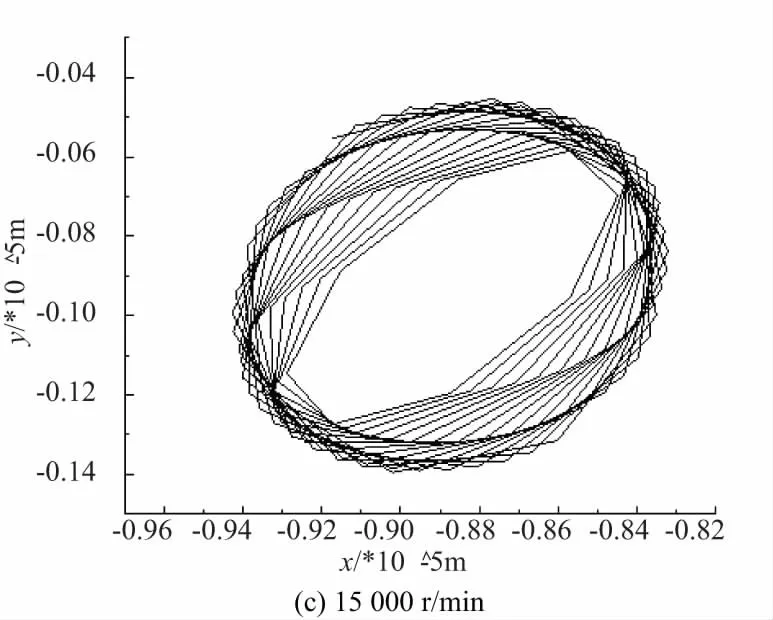
图12 试验测试得到的转子轴心运动轨迹

5 结语

1)波箔轴承支承转子的动力学特性表现为：在亚临界转速区，转子响应以周期运动为主，其间有短暂的拟周期运动和混沌运动；在临界转速区，摩擦力影响减小，转子响应为周期运动，呈现线性振动特征；在超临界转速区，响应以拟周期运动和混沌运动为主要运动形式，气膜力和摩擦力的非线性影响充分体现。

2)随转子转速的变化，响应的形态发生变化，拟周期与混沌运动的比重不断改变。在超临界转速区，一般转速越高，拟周期运动的比重越小，混沌运动的比重越大；同时，转速的增加会导致转子振幅的增大，该波箔气体轴承空载时的极限转速约为90 000r/min。

3)波箔轴承支承的转子在升速过程中，在亚临界转速区会受到摩擦力影响，在临界转速区会有强烈的振动，当转速过高时，轴承的稳定性和承载能力均会下降。因此，波箔轴承的工作转速需要控制在超临界转速区且转速不能过高，减小非线性振动的影响。